山东省淄博市2006—2007学年度第一次模拟考试高三数学(理科)
| 题号 | 一 | 二 | 三 | 总分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 分数 | |||||||||
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至9页,共150分。考试时间120分钟。考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)
注意事项:
1. 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。不能答在试卷上。
一、选择题:本大题共8小题。每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.![]() 等于
( D
)
等于
( D
)
A.2-2i B.2+2i C.-2 D.2
2.已知(![]() )
)![]() 的展开式中,不含x的项是
的展开式中,不含x的项是![]() ,那么正数p的值是
( C )
,那么正数p的值是
( C )
A. 1 B.2 C.3 D.4
3.在![]() 中,已知sinC=2sin(B+C)cosB,那么
中,已知sinC=2sin(B+C)cosB,那么![]() 一定是
( B )
一定是
( B )
A.等腰直角三角形 B.等腰三角形 C.直角三角形 D.等边三角形
4.已知直线![]() 上一点P的横坐标为a,有两个点A(-1,1),B(3,3),那么使向量
上一点P的横坐标为a,有两个点A(-1,1),B(3,3),那么使向量![]() 与
与![]() 夹角为钝角的一个充分但不必要的条件是
( B )
夹角为钝角的一个充分但不必要的条件是
( B )
A.-1<a<2 B.0<a<1 C.![]() D.0<a<2
D.0<a<2
5.若指数函数![]() 的部分对应值如下表:
的部分对应值如下表:
| x | -2 | 0 |
|
| 0.592 | 1 |
则不等式![]() (x)<0的解集为
( D )
(x)<0的解集为
( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.有一排7只发光二级管,每只二级管点亮时可发出红光或绿光,若每次恰有3只二级管点亮,但相邻的两只二级管不能同时点亮,根据这三只点亮的二级管的不同位置或不同颜色来表示不同的信息,则这排二级管能表示的信息种数共有 (D)
A.10 B.48 C.60 D.80
7.设f(x)是定义在实数集R上的函数,满足f(0)=1,且对任意实数a,b都有f(a) -f(a-b)= b(2a-b+1),则f(x)的解析式可以为是 ( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
8.已知![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,
的等比数列,![]()
![]() ,
,![]() ,(其中
,(其中![]() 表示
表示![]() 的最大整数,如[2.5]=2).如果数列
的最大整数,如[2.5]=2).如果数列![]() 有极限,那么公比
有极限,那么公比![]() 的取值范围是
( C )
的取值范围是
( C )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
淄博市2006—2007学年度第一次模拟考试高三数学(理科)
第Ⅱ卷(共110分)
注意事项:
1.用钢笔或圆珠笔将答案直接写在试卷上。
2.答卷前将密封线内的项目填写清楚。
| 得分 | 评卷人 |
|
|
|
二、填空题:本大题共6小题,每小题5分,共30分。把答案填在 题中横线上。
9.某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2:3:4,现用分层抽样方法抽出一个容量为![]() 的样本,样本中A种型号产品有16件.那么此样本的容量
的样本,样本中A种型号产品有16件.那么此样本的容量![]() =
.
=
.
10.若焦点在![]() 轴上的椭圆
轴上的椭圆![]() 的离心率为
的离心率为![]() ,则m=_________.
,则m=_________.
11.如果过点(0,1)斜率为k的直线l与圆![]() 交于M、N两点,
交于M、N两点,
且M、N关于直线x+y=0对称,那么直线l的斜率k=_____________;不等式组 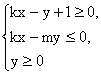 表示的平面区域的面积是_____________.
表示的平面区域的面积是_____________.
12.设函数f(x)=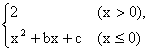 ,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)=______________,关于x的方程f(x)= x的解的个数为___________.
,若f(-4)=f(0),f(-2)=-2,则f(x)的解析式为f(x)=______________,关于x的方程f(x)= x的解的个数为___________.
13.已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,则球的半径等于_________,球的表面积等于__________.
14.设函数f(x)=sin(wx+![]() )(w>0,-
)(w>0,-![]() <
<![]() <
<![]() ,给出以下四个结论:
,给出以下四个结论:
①它的周期为π;
②它的图象关于直线x=![]() 对称;
对称;
③它的图象关于点(![]() ,0)对称; ④在区间(-
,0)对称; ④在区间(-![]() ,0)上是增函数.
,0)上是增函数.
以其中两个论断为条件,另两个论断作结论写出你认为正确的一个命题:____.
(注:填上你认为是正确的一种答案即可)
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
| 得分 | 评卷人 |
|
|
|
15.(本小题满分13分)
学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设![]() 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且![]() .
.
(I) 求文娱队的人数;
(II) 写出![]() 的概率分布列并计算
的概率分布列并计算![]() .
.
| 得分 | 评卷人 |
|
|
|
16.(本小题满分13分)
已知函数![]() ,曲线
,曲线![]() 在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
在点x=1处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为![]() ,若
,若![]() 时,
时,![]() 有极值.
有极值.
(I) 求a、b、c的值;
(II) 求![]() 在[-3,1]上的最大值和最小值.
在[-3,1]上的最大值和最小值.
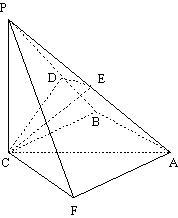
17.(本小题满分14分)
如图,三棱锥P—ABC中, PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD![]() 平面PAB.
平面PAB.
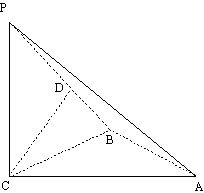 (I) 求证:AB
(I) 求证:AB![]() 平面PCB;
平面PCB;
(II) 求异面直线AP与BC所成角的大小;
(III)求二面角C-PA-B的大小.
18.(本小题满分13分)设A,B分别是直线![]() 和
和![]() 上的两个动点,并且
上的两个动点,并且![]() ,动点P满足
,动点P满足![]() .记动点P的轨迹为C.
.记动点P的轨迹为C.
(I) 求轨迹C的方程;
(II)若点D的坐标为(0,16),M、N是曲线C上的两个动点,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
19.(本小题满分13分)已知![]() ,
,![]() ,数列
,数列![]() 满足
满足![]() ,
,
![]() ,
, ![]() .
.
(Ⅰ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅱ)当n取何值时,![]() 取最大值,并求出最大值;
取最大值,并求出最大值;
(III)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
20.(本小题满分14分)已知函数![]() ,( x>0).
,( x>0).
(I)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(II)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb]
(m≠0),求m的取值范围.
淄博市2006—2007学年度第一次模拟考试
高三数学参考答案 (理科)
一、选择题(本大题共8小题,每小题5分,共40分)
1.D 2.C 3.B 4.B 5.D 6.D 7.A 8.C
二、填空题(本大题共6小题,每小题5分,共30分)
9.72 10.![]() 11.1 ,
11.1 ,![]() 12.f(x)=
12.f(x)=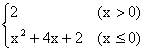 ,3
,3
13.![]() ,
,![]() 14.①②
14.①②![]() ③④ , ①③
③④ , ①③![]() ②④
②④
注:两个空的填空题第一个空填对得2分,第二个空填对得3分.
三、解答题(本大题共6小题,共80分)
15.(本小题满分13分)
解:设既会唱歌又会跳舞的有x人,则文娱队中共有(7-x)人,那么只会一项的人数是
(7-2 x)人.
(I)∵![]() ,
,
∴![]() .……………………………………3分
.……………………………………3分
即![]() .
.
∴![]() .
.
∴x=2. ……………………………………5分
故文娱队共有5人.……………………………………7分
(II) ![]() 的概率分布列为
的概率分布列为
|
| 0 | 1 | 2 |
| P |
|
|
|
![]() ,……………………………………9分
,……………………………………9分
![]() ,……………………………………11分
,……………………………………11分
∴![]() =1. …………………………13分
=1. …………………………13分
16.(本小题满分13分)
解:(I)由![]() ,得
,得
![]() .……………………………………2分
.……………………………………2分
当x=1时,切线l的斜率为3,可得2a+b=0. ①
当![]() 时,
时,![]() 有极值,则
有极值,则![]() ,可得4a+3b+4=0.②
,可得4a+3b+4=0.②
由①、②解得 a=2,b=-4.……………………………………5分
设切线l的方程为 ![]() .
.
由原点到切线l的距离为![]() ,
,
则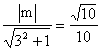 .解得m=±1.
.解得m=±1.
∵切线l不过第四象限,
∴m=1.……………………………………6分
由于l切点的横坐标为x=1,∴![]() .
.
∴1+a+b+c=4.
∴c=5.…………………………………………………………………7分
(II)由(I)可得![]() ,
,
∴![]() .……………………………………8分
.……………………………………8分
令![]() ,得x=-2,
,得x=-2, ![]() .
.
| x | [-3,-2) | -2 | (-2, |
| ( |
|
| + | 0 | - | 0 | + |
| f(x) |
| 极大值 |
| 极小值 |
|
……………………………………11分
∴f(x)在x=-2处取得极大值f(-2)=13.
在![]() 处取得极小值
处取得极小值![]() =
=![]() .
.
又f(-3)=8,f(1)=4.
∴f(x)在[-3,1]上的最大值为13,最小值为![]() .……………………………………13分
.……………………………………13分
17.(本小题满分14分)
解法一:(I) ∵PC![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
∴PC![]() AB.…………………………2分
AB.…………………………2分
 ∵CD
∵CD![]() 平面PAB,
平面PAB,![]() 平面PAB,
平面PAB,
∴CD![]() AB.…………………………4分
AB.…………………………4分
又![]() ,
,
∴AB![]() 平面PCB. …………………………5分
平面PCB. …………………………5分
(II) 过点A作AF//BC,且AF=BC,连结PF,CF.
则![]() 为异面直线PA与BC所成的角.………6分
为异面直线PA与BC所成的角.………6分
由(Ⅰ)可得AB⊥BC,
∴CF![]() AF.
AF.
由三垂线定理,得PF![]() AF.
AF.
则AF=CF=![]() ,PF=
,PF=![]() ,
,
在![]() 中, tan∠PAF=
中, tan∠PAF=![]() =
=![]() ,
,
∴异面直线PA与BC所成的角为![]() .…………………………………9分
.…………………………………9分
(III)取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE ![]() PA,CE=
PA,CE=![]() .
.
∵CD![]() 平面PAB,
平面PAB,
由三垂线定理的逆定理,得 DE ![]() PA.
PA.
∴![]() 为二面角C-PA-B的平面角.…………………………………11分
为二面角C-PA-B的平面角.…………………………………11分
由(I) AB![]() 平面PCB,又∵AB=BC,可求得BC=
平面PCB,又∵AB=BC,可求得BC=![]() .
.
在![]() 中,PB=
中,PB=![]() ,
,
![]() .
.
 在
在![]() 中, sin∠CED=
中, sin∠CED=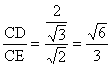 .
.
∴二面角C-PA-B的大小为arcsin![]() .……14分
.……14分
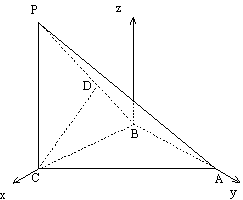
解法二:(I)同解法一.
(II) 由(I) AB![]() 平面PCB,∵PC=AC=2,
平面PCB,∵PC=AC=2,
又∵AB=BC,可求得BC=![]() .
.
以B为原点,如图建立坐标系.
则A(0,![]() ,0),B(0,0,0),
,0),B(0,0,0),
C(![]() ,0,0),P(
,0,0),P(![]() ,0,2).
,0,2).
![]() ,
,![]() .
.
…………………7分
则![]() +0+0=2.
+0+0=2.
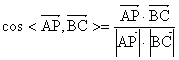 =
=![]() =
= ![]() .
.
∴异面直线AP与BC所成的角为![]() .………………………10分
.………………………10分
(III)设平面PAB的法向量为m= (x,y,z).
![]() ,
,![]() ,
,
则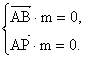 即
即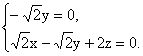
![]()
解得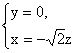 令
令![]() = -1, 得 m= (
= -1, 得 m= (![]() ,0,-1).
,0,-1).
设平面PAC的法向量为n=(![]() ).
).
![]() ,
,![]() ,
,
则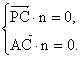 即
即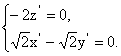
解得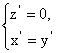 令
令![]() =1, 得 n= (1,1,0).……………………………12分
=1, 得 n= (1,1,0).……………………………12分
![]() =
=![]() .
.
∴二面角C-PA-B的大小为arccos![]() .………………………………14分
.………………………………14分
18.(本小题满分13分)
解:(I)设P(x,y),因为A、B分别为直线![]() 和
和![]() 上的点,故可设
上的点,故可设
![]() ,
,![]() .
.
∵![]() ,
,
∴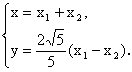 ∴
∴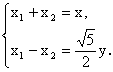 ………………………4分
………………………4分
又![]() ,
,
∴![]() .……………………………………5分
.……………………………………5分
∴![]() .
.
即曲线C的方程为![]() .………………………………………6分
.………………………………………6分
(II) 设N(s,t),M(x,y),则由![]() ,可得(x,y-16)=
,可得(x,y-16)=![]() (s,t-16).
(s,t-16).
故![]() ,
,![]() .……………………………………8分
.……………………………………8分
∵M、N在曲线C上,
∴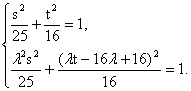 ……………………………………9分
……………………………………9分
消去s得 ![]() .
.
由题意知![]() ,且
,且![]() ,
,
解得 ![]() .………………………………………………………11分
.………………………………………………………11分
又 ![]() , ∴
, ∴![]() .
.
解得
![]() (
(![]() ).
).
故实数![]() 的取值范围是
的取值范围是![]() (
(![]() ).………………………………13分
).………………………………13分
19.(本小题满分13分)
解:(I)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
即![]() .
.
又![]() ,可知对任何
,可知对任何![]() ,
,![]() ,
,
所以![]() .……………………………2分
.……………………………2分
∵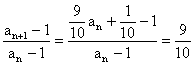 ,
,
∴![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列.………4分
的等比数列.………4分
(II)由(I)可知![]() =
=![]() (
(![]() ).
).
∴![]() .
.
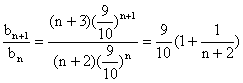 .……………………………5分
.……………………………5分
当n=7时,![]() ,
,![]() ;
;
当n<7时,![]() ,
,![]() ;
;
当n>7时,![]() ,
,![]() .
.
∴当n=7或n=8时,![]() 取最大值,最大值为
取最大值,最大值为![]() .……8分
.……8分
(III)由![]() ,得
,得![]() (*)
(*)
依题意(*)式对任意![]() 恒成立,
恒成立,
①当t=0时,(*)式显然不成立,因此t=0不合题意.…………9分
②当t<0时,由![]() ,可知
,可知![]() (
(![]() ).
).
而当m是偶数时![]() ,因此t<0不合题意.…………10分
,因此t<0不合题意.…………10分
③当t>0时,由![]() (
(![]() ),
),
∴![]() ∴
∴![]() . (
. (![]() )……11分
)……11分
设![]() (
(![]() )
)
∵![]() =
=![]() ,
,
∴![]() .
.
∴![]() 的最大值为
的最大值为![]() .
.
所以实数![]() 的取值范围是
的取值范围是![]() .…………………………………13分
.…………………………………13分
20.(本小题满分14分)
解:(I) ∵x>0,∴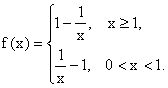
∴f(x)在(0,1)上为减函数,在![]() 上是增函数.
上是增函数.
由0<a<b,且f(a)=f(b),
可得 0<a![]() 1<b和
1<b和![]() .
.
即![]() .
.
∴2ab=a+b>![]() .……………………………………3分
.……………………………………3分
故![]() ,即ab>1.……………………………………4分
,即ab>1.……………………………………4分
(II)不存在满足条件的实数a,b.
若存在满足条件的实数a,b,使得函数y=![]() 的定义域、值域都是
的定义域、值域都是
[a,b],则a>0.
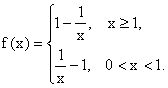
① 当![]() 时,
时,![]() 在(0,1)上为减函数.
在(0,1)上为减函数.
故![]() 即
即 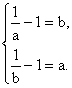
解得 a=b.
故此时不存在适合条件的实数a,b.………………………………6分
② 当![]() 时,
时,![]() 在
在![]() 上是增函数.
上是增函数.
故![]() 即
即 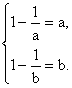
此时a,b是方程![]() 的根,此方程无实根.
的根,此方程无实根.
故此时不存在适合条件的实数a,b.………………………………8分
③ 当![]() ,
,![]() 时,
时,
由于![]() ,而
,而![]() ,
,
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b.………………………………10分
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
① 当![]() 时,由于f(x)在(0,1)上是减函数,故
时,由于f(x)在(0,1)上是减函数,故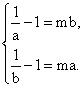 .此时刻得a,b异号,不符合题意,所以a,b不存在.
.此时刻得a,b异号,不符合题意,所以a,b不存在.
② 当![]() 或
或![]() 时,由(II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
时,由(II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
故只有![]() .
.
∵![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() 即
即 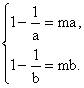
a, b是方程![]() 的两个根.
的两个根.
即关于x的方程![]() 有两个大于1的实根.……………………12分
有两个大于1的实根.……………………12分
设这两个根为![]() ,
,![]() .
.
则![]() +
+![]() =
=![]() ,
,![]() ·
·![]() =
=![]() .
.
∴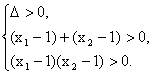 即
即 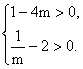
解得 ![]() .
.
故m的取值范围是![]() .…………………………………………14分
.…………………………………………14分