2006年江苏省对口单独招生数学试卷
试卷Ⅰ(共48分)
一. 选择题(本大题共12小题,每小题4分,共48分,每小题列出的四个选项中,只有一项是符合要求的)
1.已知集![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B.
![]()
C.
![]() D.
D. ![]()
2.若函数![]() 与
与![]() 互为反函数,则
互为反函数,则![]() 的值分别为( )
的值分别为( )
A.4,-2
B. 2,-2
C. -8, ![]() D.
D. ![]() ,-8
,-8
3.已知向量![]() 与
与![]() ,若
,若![]() 与
与![]() 垂直,则实数
垂直,则实数![]() 等于( )
等于( )
A.-1 B. -10 C. 2 D. 0
4.如果事件![]() 与
与![]() 互斥,那么 ( )
互斥,那么 ( )
A. ![]() 与
与![]() 是对立事件
B.
是对立事件
B. ![]() 是必然事件
是必然事件
C. ![]() 是必然事件
D.
是必然事件
D. ![]() 互不相容
互不相容
5.若数列![]() 的通项为
的通项为![]() ,则其前10项的和
,则其前10项的和![]() 等于 ( )
等于 ( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6.已知![]() ,且
,且![]() ,则
,则![]() 为( )
为( )
A.2
B. -2
C. ![]() D.
D. ![]()
7.已知![]() ,
,![]() (
(![]() ) ,若
) ,若![]() ,则
,则![]() 与
与
![]() 在同一坐标系内的图象可能是 ( )
在同一坐标系内的图象可能是 ( )
8.过点![]() ,且在两坐标上的截距之和为0的直线有几条? ( )
,且在两坐标上的截距之和为0的直线有几条? ( )
A. 1条 B. 2条 C. 3条 D. 4条
9.三个数![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B. ![]()
C.![]() D.
D. ![]()
10.![]() 的 ( )
的 ( )
A.充要条件 B. 必要而非充分条件
充分而非必要条件 D. 以上均不对
11.直线![]() 与圆
与圆![]() 相切,则
相切,则![]() 的值为 ( )
的值为 ( )
A.1或-19
B. -1或19 C. 1
D. ![]()
12.已知函数![]() 在
在![]() 上是偶函数,且
上是偶函数,且![]() 在
在![]() 上又是减函数,那么
上又是减函数,那么![]() 与
与![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B. ![]()
C.![]() D.
D. ![]()
试卷Ⅱ(102分)
二 填空题(本大题共6小题,每小题4分,共24分,把答案填在题中的横线上)
13.已知复数![]() ,
,![]() ,则
,则![]() .
.
14. 设等比数列![]() 满足
满足 ![]() ,则公比
,则公比![]() .
.
15. 若函数![]() 的图象经过点
的图象经过点![]() ,则函数
,则函数![]() 的图象必经过点 .
的图象必经过点 .
16. 方程![]() 在区间
在区间![]() 内的解的个数为
.
内的解的个数为
.
17. 由数字0,1,2,3组成的没有重复数字的四位偶数共有 .
18. 椭圆![]() 的离心率是方程
的离心率是方程![]() 的根,则
的根,则![]() .
.
三.解答题(本大题共7题,共78分)
19. (本题满分8分)解不等式:
![]()
20. (本题满分8分)已知![]() 中,满足
中,满足![]() .试判断
.试判断![]() 是什么形状?
是什么形状?
21.(本题满分14分)某公司年初花费72万元购进一台设备, 并立即投入使用. 计划第一年维护费用为8万元,从第二年开始,每一年所需维护费用比上一年增加4万元。现已知设备使用后,每年创造的收入为46万元,如果设备使用![]() 年后的累计盈利额为
年后的累计盈利额为![]() 万元。求:
万元。求:
(1)写出![]() 与
与![]() 之间的函数关系式;(累计盈利额=累计收入-累计维护费-设备购置费)
之间的函数关系式;(累计盈利额=累计收入-累计维护费-设备购置费)
(2)从第几年开始,该设备开始盈利(即累计盈利额为正值)?
(3)使用若干年后,对该设备的处理方案有两种:当年平均盈利额达到最大值时,以42万元价格处理该设备;当累计盈利额达到最大值时,以10万元的价格处理该设备,问哪种处理方法较为合算?请说明你的理由.
22.(本题满分14分)在10件产品中有2件次品,连续抽3次,每次抽1件,
(1)在放回抽样的情况下,求抽到次品数![]() 的分布列和
的分布列和![]() ;
;
(2)在不放回抽样的情况下,求抽到次品数![]() 的分布列,并
的分布列,并![]() .
.
23 (本题满分14分)在四面体![]() 中,
中,![]() ,
,![]() 为正三角形,
为正三角形,![]() 的中点,设
的中点,设![]() 。
。
(1)如何在![]() 上找一点
上找一点![]() ,使
,使![]() ?请说明理由;
?请说明理由;
(2)求点![]() 到面
到面![]() 的距离;
的距离;
(3)对于(1)中的点![]() ,求二面角
,求二面角![]() 的大小.
的大小.
24 (本题满分14分)已知动点![]() 到定直线
到定直线![]() 与定点
与定点![]() 的距离相等.
的距离相等.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)记定直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,(1)中的轨迹方程上两点
,(1)中的轨迹方程上两点![]() 满足条件:
满足条件:
![]() 成等差数列,求弦
成等差数列,求弦![]() 中点的横坐标;
中点的横坐标;
(3)设(2)中弦![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,求
,求![]() 的取值范围.
的取值范围.
25 (本题满分6分)试构造:
(1)一个周期为![]() 且是偶函数的三角函数;
且是偶函数的三角函数;
(2)一个在![]() 上单调增且为奇函数的三角函数.
上单调增且为奇函数的三角函数.
答案
一.选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | A | C | D | A | B | B | B | C | D | D |
二.填空题
13.
![]() 14.
14. ![]() 15. (-4,-2) 16.
15. (-4,-2) 16. ![]() 17. 10 18. 72
17. 10 18. 72
三.解答题
19.解:由 ![]() =
=![]() 3分
3分
得 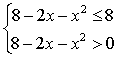 即
即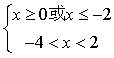 3分
3分
综合得![]() 2分
2分
20. ![]() ,
,
![]() .
3分
.
3分
设![]() ,
,
由余弦定理,得![]() ,
3分
,
3分
![]()
![]() 为钝角,即
为钝角,即![]() 是钝角三角形.
2分
是钝角三角形.
2分
21.⑴![]() ,所以
,所以![]() 的分布列为: 4分
的分布列为: 4分
|
| 0 | 1 | 2 | 3 |
|
| 0.512 | 0.384 | 0.096 | 0.008 |
![]() =1-
=1-![]() =0.488
3分
=0.488
3分
⑵
|
| 0 | 1 | 2 |
|
|
|
|
|
4分
![]()
![]() 3分
3分
22.⑴使用![]() 年后,累计总收入为 46
年后,累计总收入为 46![]() (万元)
(万元)
使用![]() 年后,累计维护费为
年后,累计维护费为![]() (万元)
(万元)
由题意得![]() 4分
4分
⑵盈利额为正,即![]() ,解得
,解得 ![]()
所以 从第三年年初开始盈利 4分
⑶第一种处理方案:年平均盈利为![]()
![]()
当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.
当![]() 时,
时, ![]() 达到最大值为16万元.获利16*6+42=138万元
达到最大值为16万元.获利16*6+42=138万元
第二种处理方案:累计盈利额为![]() 万元
万元
当![]() 时,
时, ![]() 达到最大值128万元.获利128+10=138万元
达到最大值128万元.获利128+10=138万元
两方案获利相同,但方案一的花费时间较长,所以按第一方案处理合算. 6分
23.⑴取![]() 的中点记为
的中点记为![]() ,即可.
,即可.
由于![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
![]() .
4分
.
4分
⑵ 连接![]() ,
,![]()
![]()
又![]()
![]()
![]() 5分
5分
⑶![]() ,连接
,连接![]()
![]()
![]()
又![]() ,
,![]()
![]() 为矩形
为矩形
![]() 又已知
又已知![]()
![]()
![]() .
5分
.
5分
24.⑴由题意得![]()
即![]() 轨迹方程表示为抛物线
4分
轨迹方程表示为抛物线
4分
⑵由题⑴知点![]() 为抛物线的焦点,直线
为抛物线的焦点,直线![]() 为抛物线的准线,则点
为抛物线的准线,则点![]() 坐标为
坐标为![]() .设
.设![]() ,
,![]() 则由抛物线的性质得:
则由抛物线的性质得:
![]() ,
,![]() ,
,![]()
由等差数列性质得 ![]() 即
即![]()
解得![]() 中点坐标为
中点坐标为![]() 4分
4分
⑶由题意得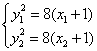
![]()
![]()
当![]() 时,由
时,由![]() 得
得![]() 则
则
![]()
![]()
![]() 的垂直平分线为
的垂直平分线为![]() ,即
,即![]() 轴 , 所以
轴 , 所以 ![]()
当![]() 时,
时, ![]() 的斜率为
的斜率为![]()
![]() 即
即![]()
又点![]() 在直线
在直线![]() 上
上 ![]()
![]()
由于弦![]() 中点
中点![]() 在抛物线内
在抛物线内
![]()
![]() 6分
6分
25.⑴(略) 3分
⑵(略) 3分