泗洪县洪翔中学高三第四次月考数学试卷2005.12.30
一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)
1.已知集合A={x
}，则集合A的真子集个数为:
A.2个 B.1个 C.4个 D.3个
2．已知函数
是偶函数, 则函数
图象的对称轴为直线：
A.
B.
C.
D.
3．在等比数列
中，
，
，则
的值为：
A．
B．
C．
D．
4．与圆
相切，且在x轴与y轴上的截距相等的直线有：
A.1条 B.2条 C.3条 D. 4条
5．已知数列
中，
，
，且满足
（
），则
A．16 B．
C．32
D．
6．函数
的图像按向量
平移后，所得函数的解析式是
，则等于：
A.
B.
C.
D．
7．将一张画了直角坐标系且两轴的长度单位相同的纸折叠一次，使点（2，0）与点（－2，4）重合，若点（7，3）与点（m ,n）重合，则m+n的值为：
A．4 B．－4 C．10 D．－10
8．直线
的方向向量的坐标为（1，k），倾斜角为
，若
，则的取值范围是：
A.
B．
C．
D．
9. 若
，则下列不等式：①
；②
；③
；④
中，正确的不等式有：
A．1个 B．2个 C．3个 D．4个
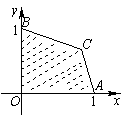10.如图，目标函数
仅在封闭区域
内（包括边界）的点
处取得最大值，则
的取值范围是：
A.
B.
C.
D.
11.在R上定义运算
：
.若不等式
对任意实数
成立，则
A．
B．
C．
D．
12.已知定义在R上的函数
满足下列三个条件：
①对任意的x∈R都有
②对于任意的
，都有
③
的图象关于y轴对称．则下列结论中，正确的是
A．
B． 
C．
D．
二．填空题(本大题共6小题，每小题4分，共24分)
13．若
是锐角，且
，则
的值是 ▲ ．
14．函数
的反函数的定义域为 ▲ ．
15．在
和
之间插入三个数，使这五个数成等比数列，则插入的三个数的乘积为_ ▲___．
16．若向量
、
的夹角为150°,││=
,││=4,则│2+│= ▲ ．
17.
若对任意
，恒有
，则a的取值范围是 ▲ ．
18.已知
两点，分别以
为圆心的两圆相交于
则
▲ .
三．解答题（本大题共5小题，共66分）
19．(本题满分12分) 已知函数
.
(1)若
,求函数
的值.
(2)求函数的值域.
20．(本题满分12分)设直线
与圆
交于
两点，且关于直线
对称，求不等式组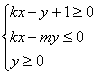
表示平面区域的面积．
21．(本题满分14分) 在△
中,
分别是角
、
、
的对边,
,
且
．
(1)求∠B的大小． (2)若
＝
，求
的最大值．
22．（本小题满分14分）某公司生产的A型商品通过租赁柜台进入某商场销售，第一年商场为吸引厂家，决定免收该年的管理费，因此，该年A型商品定价为每件70元，销售量为11.8万件；第二年商场开始对该商品征收比率为
%的管理费（即每销售100元要征收元），于是该商品的定价上升为每件
元，预计年销售量将减少万件．
(1)将第二年商场对商品征收的管理费y万元表示成的函数，并指出这个函数的定义域．
(2)要使第二年商场在此项经营中收取的管理费不少于14万元，则商场对该商品征收管理费的比率%的范围是多少？
(3)第二年，商场在所收管理费不少于14万元的前提下，要让厂家获得最大销售额，则应为多少？
23．（本小题满分14分） 对于函数 ，若存在
，使 
成立，则称
为 的“滞点”.已知函数
．
(1)试问有无“滞点”？若有，求之，否则说明理由．
(2)已知数列
的各项均为负数，且满足
,求数列的通项公式．
(3)已知
,求
的前项和
．
泗洪县洪翔中学高三第四次月考数学试卷参考答案
一．选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | D | D | B | B | C | D | C | A | C | C |
二．填空题
| 题号 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 |
|
| 216 |
|
|
|
或
19. 19。[解](1) ∵sinx=
, x∈[
,
],∴cosx=-
f(x)=2(
sinx+
cosx)-2cosx
=sinx-cosx=+
(2) f(x)= 2sin(x-
) ∵≤x≤, ∴
,
≤sin(x-)≤1 ∴函数f(x)的值域[1,2]
20．
21.解：（Ⅰ）x·y＝（2a＋c）cosB＋bcosC＝0，
由正弦定理 2sinAcosB＋sinCcosB＋sinBcosC＝0，
2sinAcosB＋sin(B＋C)＝0．
sinA(2cosB＋1)＝0．
∵A，B∈(0，π)，∴sinA≠0，cosB＝－，B＝．
（Ⅱ）法一：3＝a2＋c2－2accos＝(a＋c)2－ac，
(a＋c)2＝3＋ac≤3＋()2， ∴(a＋c)2≤4，a＋c≤2．
∴当且仅当a＝c时，(a＋c)max＝2．
法二：2R＝＝＝2，A＋C＝．
a＋c＝2(sinA＋sinC)＝2[sin(＋)＋sin(－)]
＝4sincos＝4×cos≤2．
当且仅当A＝C＝时，(a＋c)max＝2．
22. 解：（1）依题意，第二年该商品年销售量为（11.8-p）万件，年销售收入为
万元，
则商场该年对该商品征收的总管理费为
万元，
故所求函数为
.
由11.8-p>0及p>0得定义域为
（2）由
得
.
化简得
，即
，解得
.
故当比率在[2%，10%]内时，商场收取的管理费将不少于14万元.
（3）第二年，当商场的管理费不少于14万元时，厂家的销售收入为
，
因为
在区间
上为减函数，
所以
万元.
故当比率为2%时，厂家销售额最大，且商场收管理费又不少于14万元.
23. 解：（I）由
令
解得
即f(x)存在两个滞点0和2
（II）由题得
，
①
故
②
由②-①得
，
，即
是等差数列，且
当n=1时，由
(III)
③
④
由④-③得
