08届高考文科数学三月综合测试
命题人：徐喜峰（2008年03月17日）
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷（非选择题）两部分．第Ⅰ卷50分，第Ⅱ卷100分，卷面共计150分，时间120分钟.
第Ⅰ卷（选择题 共50分）
注意事项：
1．答第Ⅰ卷前，考生务必将自己的考号、班级、姓名等用钢笔或圆珠笔填写在答题卷上.
2．每小题选出答案后，用钢笔或圆珠笔填写在答题卷上.
一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的（本大题共12小题，每小题5分，共60分）
1．若全集U = R，集合
A．
B．
C．
D．
2．向量
满足
与
的夹角为60°，则
A．1 B．
C．
D．
3．
为等差数列，若
，且它的前n项和Sn有最小值，那么当Sn取得最小正值时，n =
A．11 B．17 C．19 D．21
4．不等式
的解集是
A．
B．
C．
D．（0，
）
5．设
，则
A．
B．
C．
D．
6．在
中，已知sinC=2sin(B+C)cosB,那么一定是
Ａ．等腰直角三角形 Ｂ．等腰三角形 Ｃ．直角三角形 Ｄ．等边三角形
7．某次文艺汇演，要将A、B、C、D、E、F这六个不同节目编排成节目单如下表：
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 节目 |
如果A、B两个节目要相邻，且都不排在第3号位置，那么节目单上不同的排序方式有
A．192种 B．144种 C．96种 D．72种
|
的单调递增区间，将
的图像按向量
平移得到一个新的函数
的图像，则的单调递减区间必定是
A．
B．
C．
D．
9．正三棱锥P—ABC的三条侧棱两两互相垂直，则该正三棱锥的内切球与外接球的半径之比为
A．1:3 B．
C．
D．
10．已知P是椭圆
上的点，F1、F2分别是椭圆的左、右焦点，若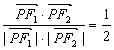
，则△F1PF2的面积为
A．
B．
C．
D．
第Ⅱ卷（非选择题 共100分）
二、填空题：把答案填在答题卡相应题号后的横线上（本大题共5小题，每小题5分，共25分）
11．已知等式
成立，则
的值等于
.
12．若曲线
在点P处切线平行于直线
，则点P的坐标为 .
|
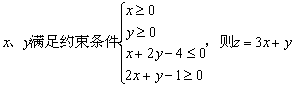的最小值是
.
14．设函数
内有定义，则下列函数
①
②
③
④
其中必为奇函数的有 （要求填写所有正确答案的序号）.
15．黄金周期间，某车站来自甲、乙两个方向的客车超员的概率分别为0.9和0.8，且旅客都需在该站转车驶往景区.据推算，若两个方向都超员，车站则需支付旅客滞留费用8千元；若有且只有一个方向超员，则需支付5千元；若都不超员，则无需支付任何费用.则车站可能支付此项费用 元（车票收入另计）.
三、解答题：解答应写出文字说明，证明过程或演算步骤（本大题共6小题，共75分）
16．（本小题满分12分）
已知
（
为常数）
（Ⅰ）求
的最小正周期；
（Ⅱ）求的单调递增区间；
（Ⅲ）若的最大值与最小值之和为3，求的值.
17．（本小题满分12分）
甲、乙、丙、丁四人做相互传球练习，第一次甲传给其他三人中的一人，第二次由拿球者再传给其他三人中的一人，……，且拿球者传给其他三人中的任何一人都是等可能的，求：
（Ⅰ）共传了四次，第四次球传回到甲的概率；
（Ⅱ）若规定：最多传五次球，且在传球过程中，球传回到甲手中即停止传球；设ξ表示传球停止时传球的次数，求
|
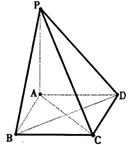
在四棱锥P—ABCD中，底面ABCD是a的正方形，
PA⊥平面ABCD，且PA=2AB
（Ⅰ）求证：平面PAC⊥平面PBD；
（Ⅱ）求二面角B—PC—D的余弦值.
|
19．（本小题满分12分）
已知数列满足：
（Ⅰ）求数列的通项公式；
（Ⅱ）若
，求数列
的前n项和Sn.
20．（本小题满分13分）
已知直线
相交于A、B两点，M是线段AB上的一点，
，且点M在直线
上.
（Ⅰ）求椭圆的离心率；
（Ⅱ）若椭圆的焦点关于直线l的对称点在单位圆
上，求椭圆的方程.
21．（本小题满分14分）
已知函数
的图象关于原点的对称，且当x = 1时，
（Ⅰ）求a、b、c、d的值；
（Ⅱ）当
时，图象上是否存在两点，使得过此两点处的切线互相垂直？试证明你的结论；
（Ⅲ）若x1，
参考答案
一、选择题：
DDCBA BBDDA
|
11．0 12．（±1，0） 13．1 14．②④ 15. 7.06
三、解答题：
16．解：
2分
（Ⅰ）
4分
（Ⅱ）由
单调递增区间为
8分
（Ⅲ）
由
12分
17．解：（Ⅰ）
6分
|
12分
18．解：（Ⅰ）证明：∵PA⊥平面ABCD ∴PA⊥BD
∵ABCD为正方形 ∴AC⊥BD
∴BD⊥平面PAC又BD在平面BPD内，
∴平面PAC⊥平面BPD 6分
（Ⅱ）解法一：在平面BCP内作BN⊥PC垂足为N，连DN，
∵Rt△PBC≌Rt△PDC，由BN⊥PC得DN⊥PC；
∴∠BND为二面角B—PC—D的平面角，
在△BND中，BN=DN=
，BD=
∴cos∠BND =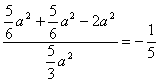
12分
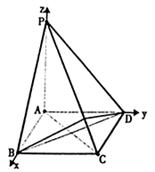
解法二：以A为原点，AB、AD、AP所在直线分别为x轴、y轴、z轴建立空间坐标系如图，在平面BCP内作BN⊥PC垂足为N连DN，
∵Rt△PBC≌Rt△PDC，由BN⊥PC得DN⊥PC；
∴∠BND为二面角B—PC—D的平面角 8分
设
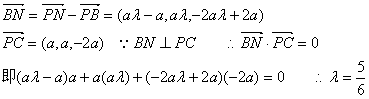
10分
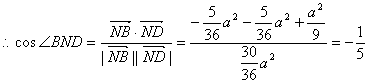12分
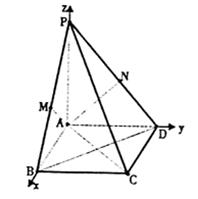
解法三：以A为原点，AB、AD、AP所在直线分别为x轴、y轴、z轴建立如图空间坐标系，作AM⊥PB于M、AN⊥PD于N，易证AM⊥平面PBC，AN⊥平面PDC，
|
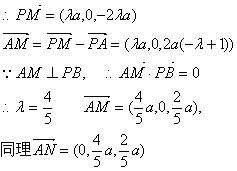
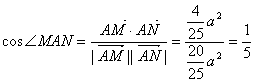10分
∵二面角B—PC—D的平面角与∠MAN互补
∴二面角B—PC—D的余弦值为
12分
19．解：（Ⅰ）
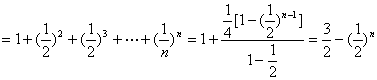4分
又∵当n = 1时，上式也成立，
6分
（Ⅱ）
8分
又
①
②
①－②得：
12分
20．解：（Ⅰ）由知M是AB的中点，
设A、B两点的坐标分别为
由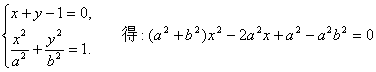
，
∴M点的坐标为
4分
又M点的直线l上：
7分
（Ⅱ）由（Ⅰ）知
，不妨设椭圆的一个焦点坐标为
关于直线l：
上的对称点为
，
则有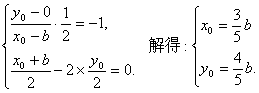
10分
由已知
，∴所求的椭圆的方程为
12分
21．解：（Ⅰ）∵函数f(x)图象关于原点对称，∴对任意实数x有
，
，
即
2分
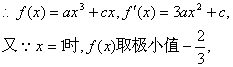
4分
（Ⅱ）当时，图象上不存在这样的两点使结论成立 5分
假设图象上存在两点，使得过此两点处的切线互相垂直，则由
，知两点处的切线斜率分别为：
此与（*）相矛盾，故假设不成立 9分
（Ⅲ）证明：
，
在[－1，1]上是减函数，且
∴在[－1，1]上，
时，
14分