2006届高三年级第二次调研试题
理 科 数 学 试 卷
考试时间:2006年3月8日下午14:30—16:30
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分,考试时间120分钟.
第Ⅰ卷(选择题 共50分)
一、选择题:(本大题共12小题,每小题5分,共60分,请把答案填入答题卡中)
1.已知![]() ,
,![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.已知相交直线![]() 都在平面
都在平面![]() 内,并且都不在平面
内,并且都不在平面![]() 内,若
内,若![]() 中至少有一条与
中至少有一条与![]() 相交;
相交;![]()
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)不充分也不必要条件
3.已知![]() ,
,![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4.当![]() 时,
时,![]() 的值为
的值为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.正方体ABCD-A1B1C1D1中,若M、N分别为AA1和BB1的中点,则异面直线CM与D1N所成角的余弦值为
![]()
6.5个人分4张同样的足球票,每人至多分一张,而且票必须分完,那么不同分法的种数是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)5
(D)5
7.已知函数![]() ,则下列结论中正确的是
,则下列结论中正确的是
(A)它的定义域是![]() (B)它是奇函数
(B)它是奇函数
(C)它的值域是![]() (D)它不是周期函数
(D)它不是周期函数
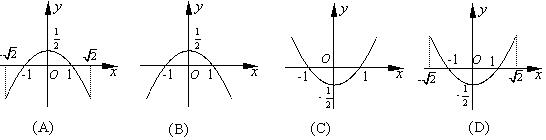
8.参数方程![]() (
(![]() 为参数)表示曲线是
为参数)表示曲线是
9.已知双曲线![]() 上一点M到右准线的距离为10,
上一点M到右准线的距离为10,![]() 为右焦点,
为右焦点,![]() 的中点,
的中点,![]() 为坐标原点,则
为坐标原点,则![]() 的长为
的长为
(A)2 (B)2或7 (C)7或12 (D)2或12
10.已知数列![]() 满足
满足![]()
(A)0
(B)1
(C)![]() (D)
(D)![]()
11.已知向量![]() 满足:对任意
满足:对任意![]() ,恒有
,恒有![]() 则向量
则向量![]() 的夹角为
的夹角为
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
12.已知数列![]() 的通项
的通项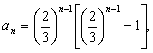 则下列表述正确的是
则下列表述正确的是
(A)最大项为![]() 最小项为
最小项为![]() (B)最大项为
(B)最大项为![]() 最小项不存在
最小项不存在
(C)最大项不存在,最小项为![]() (D)最大项为
(D)最大项为![]() 最小项为
最小项为![]()
二、填空题:(共4小题,每小题4分,共16分)tx
13.设![]()
14.设![]() 的反函数,则使
的反函数,则使![]() 成立的
成立的![]() 的取值范围是
的取值范围是
15.设![]() 满足约束条件
满足约束条件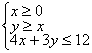 ,则
,则![]() 的取值范围是___________.
的取值范围是___________.
16.给出下面四个命题:① 若![]() 为非零向量,则
为非零向量,则![]() ; ② 若
; ② 若![]() 为一平面内两个非零向量,则
为一平面内两个非零向量,则![]() 的充要条件; ③
的充要条件; ③ ![]() 为
为![]() 所在平面内一点,且满足
所在平面内一点,且满足![]() ,则
,则![]() ; ④ 在空间四边形
; ④ 在空间四边形![]() 中,
中,![]() 分别是
分别是![]() 的中点,则
的中点,则![]() 。其中正确命题序号为__________.
。其中正确命题序号为__________.
三、解答题(共6小题,共76分)
17.(12分)已知向量![]() (
(![]() ) 和
) 和![]() =(
=(![]() ),
),![]() .
.
(1) 求![]() 的最大值;(2)当
的最大值;(2)当![]() =
=![]() 时,求
时,求![]() 的值
的值
18.(12分)口袋里装有红色和白色共36个不同的球,且红色球多于白色球.从袋子中同时取出2个球,若是同色的概率为![]() ,求:
,求:
(1) 袋中红色、白色球各是多少?
(2) 从袋中任取3个小球,求其中红球个数的分布列与数学期望?
19.(12分)已知函数![]() (
(![]() ) ,
) ,
(Ⅰ)试确定![]() 的单调区间 ,
并证明你的结论 ;
的单调区间 ,
并证明你的结论 ;
(Ⅱ)若![]() 时 , 不等式
时 , 不等式![]() 恒成立 , 求实数
恒成立 , 求实数![]() 的取值范围.
的取值范围.
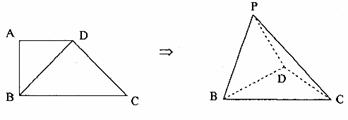
20.(12分)已知在四边形![]() 中,
中,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,将△
,将△![]() 沿对角线
沿对角线![]() 折起到如图所示
折起到如图所示![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() 。
。
(1)求证:![]() ;
;
(2)求二面角![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
 (3)求点
(3)求点![]() 到平面
到平面![]() 的距离。
的距离。
21.(本小题满分12分)如图,三条直线a、b、c两两平行,直线a、b间的距离为p,直线b、c间的距离为![]() ,A、B为直线a上两定点,且|AB|=2p,MN是在直线b上滑动的长度为2p的线段.
,A、B为直线a上两定点,且|AB|=2p,MN是在直线b上滑动的长度为2p的线段.
(1)求△AMN的外心C的轨迹E;
![]()
|
|
|

b
![]() O M N x
O M N x
![]() c
c
22.(14分)直线![]() 与
与![]() 轴、
轴、![]() 轴所围成区域内部(不包括边界)的整点个数为
轴所围成区域内部(不包括边界)的整点个数为![]() ,所围成区域内部(包括边界)的整点个数为
,所围成区域内部(包括边界)的整点个数为![]() ,(整点就是横纵坐标都为整数的点)
,(整点就是横纵坐标都为整数的点)
(1)求![]() 和
和![]() 的值;
的值;
(2)求![]() 及
及![]() 的表达式;
的表达式;
(3)对![]() 个整点用红、黄、蓝、白四色涂色,其方法总数为
个整点用红、黄、蓝、白四色涂色,其方法总数为![]() ,对
,对![]() 个整点用红、黄两色涂色,其方法总数为
个整点用红、黄两色涂色,其方法总数为![]() ,试比较
,试比较![]() 与
与![]() 的大小.
的大小.
2006届高三年级第二次调研试题
数学理科参考答案
一.选择题.
DCBDC DCDDA CA
二.填空题
13. ![]() 14.
14. 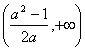 15.
15.![]() 16 . ②③④
16 . ②③④
三.解答题
17.解:(1) ![]() (2分)
(2分)
![]() =
=
![]() =
=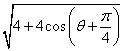 =
=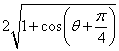 (4分)
(4分)
∵![]() , ∴
, ∴![]() ,
,
![]()
![]()
![]() 。
(6分)
。
(6分)
(2) 由已知![]() ,得
,得![]() (8分)
(8分)
又![]() ∴
∴![]() (10分)
(10分)
∵![]() ∴
∴![]() , ∴
, ∴![]() .
(12分)
.
(12分)
18. (1)令红色球为![]() 个,则依题意得
个,则依题意得![]() ,
(3分)
,
(3分)
所以![]() 得
得![]() 或
或![]() ,又红色球多于白色球,所以
,又红色球多于白色球,所以![]() .所以红色球为
.所以红色球为![]() 个,白色球为
个,白色球为![]() 个. ( 6分)
个. ( 6分)
(2)设取出红球个数为![]()
![]() ,则
,则
![]() ;
;![]() ;
;
![]() ,
, ![]() (10分)
(10分)
则![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 |
| P |
|
|
|
|
![]() (12分)
(12分)
19. 解: (1) 当![]() 时 ,
时 , ![]() , (2分)
, (2分)
令![]() 可得
可得![]() ; 令
; 令![]() 可得
可得![]() .(4分)
.(4分)
∴函数![]() (
(![]() )在区间
)在区间![]() 上是增函数;
上是增函数;
在区间![]() 上是减函数 .
(6分)
上是减函数 .
(6分)
(2) 由(Ⅰ)得,函数函数![]() (
(![]() )在区间
)在区间![]() 上是增函数 ,
上是增函数 ,
∴当![]() 时,
时, ![]() .
(8分)
.
(8分)
∵不等式![]() 恒成立 , ∴
恒成立 , ∴![]() , 解之得
, 解之得 ![]() (12分)
(12分)
20. 解法一
(1) ![]()
![]() ,
, ![]() (2分)
(2分)
又![]() .
.![]()
![]() (4分)
(4分)
(2) 过![]() 作
作![]() ,
,
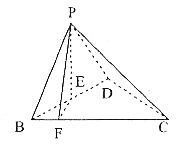 过
过![]() ,连结
,连结![]() ,由三垂线定理可证
,由三垂线定理可证![]()
![]()
![]() ,在
,在![]()
![]() ,
,
![]() 二面角
二面角![]() 的大小为
的大小为![]() . (8分)
. (8分)
(3) 设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]()
![]() ,
,![]() ,
,
![]() ,则可得:
,则可得:
![]() , 即
, 即![]() 到平面
到平面![]() 的距离为
的距离为![]() (12分)
(12分)
解法二![]()
![]() ,
,
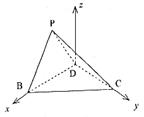
![]() .如图所示建立空间直角坐标系
.如图所示建立空间直角坐标系![]() ,
,
设![]() ,则
,则![]() .
.
(1)![]() ,
,![]() ,
,
![]() (4分)
(4分)
(2) 取平面![]() 的法向量
的法向量![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]()
![]()
![]() 即
即![]()
令![]()
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
(8分)
.
(8分)
(3) 由(2)知![]() ,
,
![]()
![]() 到平面
到平面![]() 的距离为
的距离为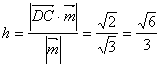 (12分)
(12分)
21、解:(1)设△AMN的外心为C(x,y),则有A(0,p)、M(x–p,0),N(x+p,0),
由题意,有|CA|=|CM| (2分)
∴![]() ,化简,得
,化简,得
x2=2py
它是以原点为顶点,y轴为对称轴,开口向上的抛物线. (4分)
(2)由(1)得,直线C恰为轨迹E的准线.
由抛物线的定义知d=|CF|,其中F(0,![]() )是抛物线的焦点.
)是抛物线的焦点.
∴d+|BC|=|CF|+|BC| (6分)
由两点间直线段最短知,线段BF与轨迹E的交点即为所求的点
直线BF的方程为![]() 联立方程组
联立方程组
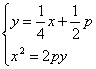 得
得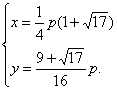 .
(10分)
.
(10分)
即C点坐标为(![]() ).
).
此时d+|BC|的最小值为|BF|=![]() .
(12分)
.
(12分)
22. 解:(1)![]() 时,直线
时,直线![]() 上有(0,0)(0,1)(0,2)(0,3)个点,直线
上有(0,0)(0,1)(0,2)(0,3)个点,直线![]() 上有(1,0)(1,1)(1,2),直线
上有(1,0)(1,1)(1,2),直线![]() 上有(2,0)(2,1),直线
上有(2,0)(2,1),直线![]() 上有(3,0)
上有(3,0)
所以![]() ……………………………4(分)
……………………………4(分)
(2)![]() 时,
时,![]() ;
;
![]() 时,
时,![]()
当![]() 时,
时,![]()
![]() 。 当
。 当![]() 时也满足。
时也满足。
所以![]() ……………9(分)
……………9(分)
(3)对于![]() 个整点中的每一个点都有4种着色方法,故
个整点中的每一个点都有4种着色方法,故![]()
对于![]() 个整点中的每一个点都有2种着色方法,故
个整点中的每一个点都有2种着色方法,故![]() ……11(分)
……11(分)
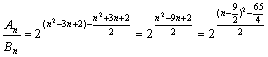
当n=1.2.3.4.5.6.7.8时![]()
当n≥9且n∈N*时,![]() …………………………………14(分)
…………………………………14(分)