苏州中学06届高三数学冲刺训练(四)
班级![]() 姓名
姓名![]() 得分
得分![]()
一、选择题:
[ ]1称集合![]() 的非空真子集的真子集叫做集合
的非空真子集的真子集叫做集合![]() 的“孙子集”,则集合
的“孙子集”,则集合![]() ={1,2,3,4,5}的孙子集共有
={1,2,3,4,5}的孙子集共有
(A)11个; (B)39个; (C)26个; (D)10个。
[ ]2各项均为实数的等比数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() 等于
(A)150;
(B)
等于
(A)150;
(B)![]() ; (C)150或
; (C)150或![]() ; (D)400或
; (D)400或![]() 。
。
[ ]3设函数![]() ,则导函数
,则导函数![]() 的展开式中
的展开式中![]() 项的系数为
项的系数为
(A)1440;
(B)![]() ; (C)
; (C)![]() ; (D)2880。
; (D)2880。
[ ]4已知平面α及以下3个几何体:①长、宽、高皆不相等的长方体;②底面为平行四边形但不是矩形的四棱锥;③正四面体。这3个几何体在平面上的射影可以是正方形的是
(A)①②③; (B)①②; (C)①③; (D)②③。
[ ]5已知两个点![]() 、
、![]() ,若直线上存在点P,使
,若直线上存在点P,使![]() ,则称该直线为“B型直线”,给出下列直线①
,则称该直线为“B型直线”,给出下列直线①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 。其中为“B型直线”的是
。其中为“B型直线”的是
(A)①③; (B)①②; (C)③④; (D)①④。
[ ]6已知函数![]() ,若经过该函数图像上的一个最大值点与一个最小值点的直线的最大斜率等于
,若经过该函数图像上的一个最大值点与一个最小值点的直线的最大斜率等于![]() ,则
,则![]() 的最小正周期为
的最小正周期为
(A)1; (B)2; (C)3; (D)4。
![]()
![]()
[ ]7设实数x、y满足不等式 ![]() ,则
,则![]() 的最小值为
的最小值为
![]()
(A)14;
(B)![]() ; (C)29;
(D)不存在。
; (C)29;
(D)不存在。
[
]8已知函数![]() 的反函数
的反函数![]() ,则
,则![]() 的图形
的图形
(A)关于点![]() 对称;
(B)关于点
对称;
(B)关于点![]() 对称;
对称;
(C)关于直线![]() 对称;
(D)关于直线
对称;
(D)关于直线![]() 对称。
对称。
[ ]9点P是椭圆![]() 上的一点,
上的一点,![]() 、
、![]() 是其两焦点,且△
是其两焦点,且△![]() 的内切圆半径是1,则当P在第一象限时,它的纵坐标是
的内切圆半径是1,则当P在第一象限时,它的纵坐标是
(A)![]() ;
(B)
;
(B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]() 。
。
[ ]10已知关于m的方程![]() 有两个绝对值都不大于1的实数根,设点
有两个绝对值都不大于1的实数根,设点![]() 是坐标平面内所对应的区域内的动点,则
是坐标平面内所对应的区域内的动点,则![]() 取值范围是
取值范围是
(A)![]() ;
(B)
;
(B)![]() ; (C)
; (C)![]() ;
(D)
;
(D)![]() 。
。
二、填空题:
11已知函数![]() 是区间
是区间![]() 上的减函数,且满足
上的减函数,且满足![]() ,
,![]() ,则不等式
,则不等式![]() <
<![]() 的解集为
的解集为![]() 。
。
12王大鹏每天骑自行车上学,从他家到学校的途中要过4个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的且概率均为![]() ,则他连续在两个交通岗遇到红灯的概率为
,则他连续在两个交通岗遇到红灯的概率为![]() 。
。
13已知函数![]() (x>1,p为正常数)与
(x>1,p为正常数)与![]() 有相同的值域,则
有相同的值域,则![]() 的值为
的值为![]() 。
。
14将正整数排成下表:1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
如果将第![]() 行第
行第![]() 列的那个数记为
列的那个数记为![]() ,则数表中的2008就记为
,则数表中的2008就记为![]() 。
。
15设![]() 的展开式中各项系数之和为A,各项的二项式系数之和为B,如果
的展开式中各项系数之和为A,各项的二项式系数之和为B,如果![]() ,则展开式中x的系数为
,则展开式中x的系数为![]() 。
。
16计算![]()
![]() 。
。
三、解答题:
17 已知函数![]() 。
。
(Ⅰ)化简![]() 并求
并求![]() 的值;
的值;
(Ⅱ)若0<α<π,![]() 求α。
求α。
18如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,
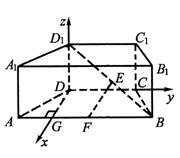 AB=2AD=2DC=2,E为BD1的中点,F为AB的中点。
AB=2AD=2DC=2,E为BD1的中点,F为AB的中点。
(Ⅰ)求证:EF∥平面ADD1 A1;
(Ⅱ)建立空间直角坐标系D-xyz (DG是AB边上的高),若BB1=![]() ,求A1F与平面DEF所成的角的大小。
,求A1F与平面DEF所成的角的大小。
19已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,一条经过点
轴上,一条经过点![]() ,方向为
,方向为![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,又
点,又![]() 。
。
(Ⅰ)求直线![]() 的方程;
的方程;
(Ⅱ)求椭圆![]() 的长轴长的取值范围。
的长轴长的取值范围。
20已知定义在R上的函数![]() 满足:对于任意实数x, y ,恒有
满足:对于任意实数x, y ,恒有![]() ,且当x>0时,
,且当x>0时,![]() 。
。
(Ⅰ)求证:![]() 且当x<0时,有
且当x<0时,有![]() ;
;
(Ⅱ)试判断函数![]() 在R上的单调性,并证明你的结论;
在R上的单调性,并证明你的结论;
(Ⅲ)若实数x、y满足:![]() 且
且![]() 求z=x+y取值范围。
求z=x+y取值范围。
21在直角坐标平面上有一点列![]() 、
、![]() 、…、
、…、![]() 、…,对每个正整数
、…,对每个正整数![]() ,点
,点![]() 位于函数
位于函数![]() 图像上,且
图像上,且![]() 横坐标构成以
横坐标构成以![]() 为首项,
为首项,![]() 为公差的等差数列
为公差的等差数列![]() 。
。
(Ⅰ)设抛物线![]() 、
、![]() 、
、![]() 、…,
、…,![]() 、…中的每一条的对称轴都垂直于
、…中的每一条的对称轴都垂直于![]() 轴,第
轴,第![]() 条抛物线
条抛物线![]() 的顶点为
的顶点为![]() 且过点
且过点![]() ,记过点
,记过点![]() 且与抛物线
且与抛物线![]() 只有一个交点的直线的斜率为
只有一个交点的直线的斜率为![]() ,求证:
,求证:![]() +…
+…![]() <
<![]() ;
;
(Ⅱ)设![]() ,
,![]() ,等差数列
,等差数列![]() 的任一项
的任一项![]() ,其中
,其中![]() 是
是![]() 中的最大数,
中的最大数,![]() <
<![]() <
<![]() ,求
,求![]() 通项公式。
通项公式。
苏州中学06届高三数学冲刺训练(四)参考答案
1C2A3C4A5B6D7A8B9A10A11、![]() >1或
>1或![]() <
<![]() ;12、
;12、![]() ;13、
;13、![]() ;14、
;14、![]() ;15、108;16、
;15、108;16、![]() ;17、
;17、![]() ;18、
;18、![]() ;
;
19、解:①![]() 即
即![]() ;
;
②设![]() 、
、![]() ,
,![]() ,由
,由![]() 得
得![]() ,将
,将![]() 代入
代入![]() 得
得![]()
由![]() >0得
>0得![]() >5,且
>5,且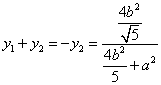 ,
,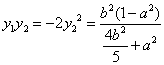 ,
,
易得![]() ,即
,即![]() ,所以
,所以![]() >5,解得
>5,解得
1<![]() <9,又焦点在
<9,又焦点在![]() 轴上,所以
轴上,所以![]() >
>![]() ,所以
,所以![]() <4
<4![]() ,从而
,从而
1<a<![]() ,故椭圆
,故椭圆![]() 的长轴长的取值范围为
的长轴长的取值范围为![]() 。
。
20、(Ⅰ)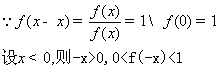
![]()
(Ⅱ)解:设![]()
![]()
![]()
![]() 在R上单调递减
在R上单调递减
(Ⅲ)![]()
![]()
![]() ①
①![]()
![]() ②
②![]() 。
。
21、解:①设![]() 即
即![]() ,∵
,∵![]() 过点
过点![]() ,
,
∴![]() ,比较系数得
,比较系数得![]() ,所以
,所以![]() ,
,
∵过点![]() 且与抛物线
且与抛物线![]() 只有一个交点的直线即为过点
只有一个交点的直线即为过点![]() 的切线,
的切线,![]() ,
,
∴![]() (
(![]() ),∴
),∴![]() +…
+…![]()
![]() +…
+…![]()
![]() <
<![]() 。
。
②∵![]() ,∴
,∴![]() 中的元素即为两个等差数列
中的元素即为两个等差数列![]() 、
、![]() 中的公共项,它们组成以
中的公共项,它们组成以![]() 为首项,
为首项,![]() 为公差的等差数列,∵
为公差的等差数列,∵
![]() 且
且![]() 是
是![]() 中的最大数,∴
中的最大数,∴![]() ,公差为
,公差为![]() 。
。
![]() 当
当![]() 时,
时,![]() ,此时
,此时![]() ,舍去;
,舍去;
![]() 当
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
![]() 当
当![]() 时,
时,![]() ,此时
,此时![]() 。
。
综上,等差数列![]() 的通项公式为
的通项公式为![]() 。
。