08届高考文科数学摸底考试试题
本卷分第Ⅰ卷(选择题、填空题)和第Ⅱ卷解答题两部分,满分150分.考试用时间120分钟.
注意事项:
1.答第I卷前,考生务必将自己的姓名、班级、学校用蓝、黑墨水钢笔签字笔写在答卷上;2.第I卷每小题得出答案后,请将答案填写在答题卷相应表格指定位置上。答在第Ⅰ卷上不得分;3.考试结束,考生只需将第Ⅱ卷(含答卷)交回。
参考公式: ![]() , 其中
, 其中![]() 是锥体的底面积,
是锥体的底面积,![]() 是锥体的高.
是锥体的高.
第Ⅰ卷(选择题、填空题共70分)
一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
![]() 设
设![]() ,则
,则![]()
![]()
2. “![]() ”是“复数
”是“复数![]()
![]() 是纯虚数”的
是纯虚数”的
![]() .必要不充分条件
.必要不充分条件 ![]() .充分不必要条件
.充分不必要条件
![]() .充要条件
.充要条件
![]() .不充分不必要条件
.不充分不必要条件
3.若抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为
的值为
![]() .
. ![]()
![]() .
. ![]()
![]() .
. ![]()
![]() .
.![]()
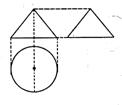 4. 如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为
4. 如右图,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
5. 设向量![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() =(2,1),3
=(2,1),3![]() +
+![]() =(5,4),则
=(5,4),则![]() =
=
![]() .
.![]()
![]() .
. ![]()
![]() .
.![]()
![]() .
.![]()
6. 在各项为正数的等比数列![]() 中,
中,![]() ,前三项和为
,前三项和为![]() ,则
,则![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
![]()
7. 函数![]() 的定义域是
的定义域是
A.(3,+∞)
B.[3, +∞)
C.![]() D.[4, +∞)
D.[4, +∞)
8. 已知:在⊿ABC中,![]() ,则此三角形为
,则此三角形为
A. 直角三角形 B. 等腰直角三角形
C. 等腰三角形 C. 等腰或直角三角形
9. 目标函数![]() ,变量
,变量![]() 满足
满足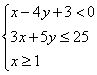 ,则有
,则有
A.![]() B.
B.![]()
![]() 无最小值
无最小值
C.![]() 无最大值 D.
无最大值 D.![]() 既无最大值,也无最小值
既无最大值,也无最小值
10.在实数集上定义运算![]() :
:![]() ,若不等式
,若不等式![]() 对任意实数
对任意实数![]() 都成立,则实数
都成立,则实数![]() 的取值范围是
的取值范围是
![]() .
.![]()
![]() .
.![]()
![]()
![]()
![]()
![]()
二、填空题(共.5小题,每小题5分,满分20分,14-15是选做题,考生只能选做一题,两题全答,只计算前一题的得分)
11.若焦点在![]() 轴的椭圆
轴的椭圆![]() 的离心率为
的离心率为![]() ,则
,则![]() 的值为_______________.
的值为_______________.
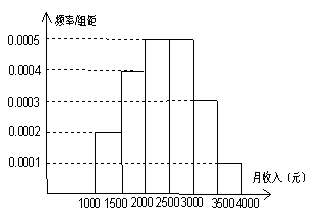
12. 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在![]() (元)/月收入段应抽出
人.
(元)/月收入段应抽出
人.
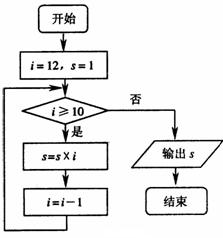
 13.下面框图表示的程序所输出的结果是_______.
13.下面框图表示的程序所输出的结果是_______.
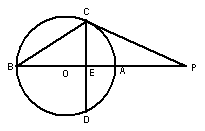
14.如图,![]() 切⊙
切⊙![]() 于点
于点![]() ,割线
,割线![]() 经过圆心
经过圆心![]() ,
,
弦![]() ⊥
⊥![]() 于点
于点![]() ,
,![]() ,
,![]() ,则
,则![]() =_______,
=_______,
![]() =___________.
=___________.
15. 圆锥曲线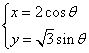 (
(![]() 是参数)和定点A(0,
是参数)和定点A(0,![]() ),F1、F2是圆锥曲线的左、右焦点,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则直线AF2的极坐标方程为 .
),F1、F2是圆锥曲线的左、右焦点,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,则直线AF2的极坐标方程为 .
第Ⅱ卷(解答题共80分)
三、解答题(共6小题,共80分)
16.(本题满分12分)
已知函数![]()
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)求函数![]() 的单调减区间.
的单调减区间.
17.(本题满分12分)
|
|
(Ⅱ)甲、乙两人不在同一站点下车的概率.
18(本题满分14分)
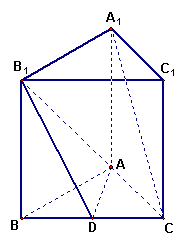 如图,在直三棱柱(侧棱与底面垂直的三棱柱)
如图,在直三棱柱(侧棱与底面垂直的三棱柱)![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点.
边的中点.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() ∥ 面
∥ 面![]() ;
;
19.(本题满分14分)
已知圆![]() 方程为:
方程为:![]() .
.
(Ⅰ)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)过圆![]() 上一动点
上一动点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
20.(本题满分14分)
已知函数![]() (
(![]() 为实数).
为实数).
(I)若![]() 在
在![]() 处有极值,求
处有极值,求![]() 的值;
的值;
(II)若![]() 在
在![]() 上是增函数,求
上是增函数,求![]() 的取值范围.
的取值范围.
21.(本题满分14分)
设函数![]() 的定义域为R,当x<0时,
的定义域为R,当x<0时,![]() >1,且对任意的实数x,y∈R,有
>1,且对任意的实数x,y∈R,有![]() .
.
(Ⅰ)求![]() ,判断并证明函数
,判断并证明函数![]() 的单调性;
的单调性;
(Ⅱ)数列![]() 满足
满足![]() ,且
,且![]()
①求![]() 通项公式.
通项公式.
②当![]() 时,不等式
时,不等式![]() 对不小于2的正整数恒成立,求x的取值范围.
对不小于2的正整数恒成立,求x的取值范围.
参考答案及评分标准
一、选择题
BACAD CCCDC
二、填空题
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
| 25 | 1320 | 2, |
|
三、解答题
16(Ⅰ).解: ![]() ……………………………3分
……………………………3分
所以![]() ……………………………………………………6分
……………………………………………………6分
(Ⅱ)解:由![]() (
(![]() ),…………………………..9分
),…………………………..9分
得![]() (
(![]() )
)
所以,减区间为![]() (
(![]() )…………………………….12分
)…………………………….12分
17.(Ⅰ)基本事件是甲在Ai(i=1,2,3,4,5)下车
∴基本事件为n=5.………………………………………………………………3分
记事件A=“甲在A2站点下车”,
则A包含的基本事件数为m=1,
![]() ………………………………………………………………6分
………………………………………………………………6分
(Ⅱ)基本事件的总数为n=5×5=25.…………………………………………8分
记事件B=“甲、乙两人在同一站点下车”,
则B包含的基本事件数为k=5,
![]() ………………………………………………………………10分
………………………………………………………………10分
所以甲、乙两人不在同一站点下车的概率为![]() ………………12分
………………12分
18. 证明:(I)直三棱柱![]() ,底面三边长
,底面三边长![]() ,
,![]() ,
,![]()
∴ ![]() ,………………………………………………..2分
,………………………………………………..2分
又![]() ,
,
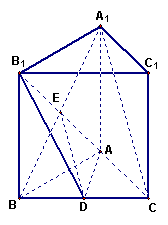 ∴
∴![]()
![]()
![]()
![]()
![]()
![]() 面
面![]() …………………………………….5分
…………………………………….5分
∴![]() ………………………………………….7分
………………………………………….7分
(II)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ………….9分
………….9分
∵ ![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,∴
的中点,∴ ![]() …………11分
…………11分
∵ ![]() ,
,![]() ,∴
,∴![]() ………..14分
………..14分
19.解:(Ⅰ)①当直线![]() 垂直于
垂直于![]() 轴时,则此时直线方程为
轴时,则此时直线方程为![]() ,
,![]() 与圆的两个交点坐标为
与圆的两个交点坐标为![]() 和
和![]() ,其距离为
,其距离为![]() , 满足题意…………………………..2分
, 满足题意…………………………..2分
②若直线![]() 不垂直于
不垂直于![]() 轴,设其方程为
轴,设其方程为![]() ,即
,即![]()
设圆心到此直线的距离为![]() ,则
,则![]() ,得
,得![]()
∴![]() ……………………………………………………5分
……………………………………………………5分
![]() ,故所求直线方程为
,故所求直线方程为![]()
综上所述,所求直线为![]() 或
或![]() …………………………..7分
…………………………..7分
(Ⅱ)设点![]() 的坐标为
的坐标为![]() (
(![]() ),
),![]() 点坐标为
点坐标为![]()
则![]() 点坐标是
点坐标是![]() ……………………………………….8分
……………………………………….8分
∵![]() ,
,
∴![]() 即
即![]() ,
,![]()
![]() ………………………..10分
………………………..10分
又∵![]() ,∴
,∴![]()
∴![]() 点的轨迹方程是
点的轨迹方程是![]() …………………………………13分
…………………………………13分
轨迹是一个焦点在![]() 轴上的椭圆,除去短轴端点。…………………………14分
轴上的椭圆,除去短轴端点。…………………………14分
20. (I)解:由已知得![]() 的定义域为
的定义域为![]()
又![]() ……3分
……3分
![]() 由题意得
由题意得![]()
![]() ……6分
……6分
(II)解:依题意得
![]() 对
对![]() 恒成立,
恒成立,![]() ……8分
……8分
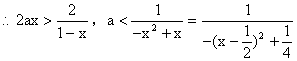 ……10分
……10分
![]() 的最大值为
的最大值为![]()
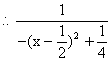 的最小值为
的最小值为![]() ……12分
……12分
又因![]() 时符合题意
时符合题意
![]() 为所求 ……14分
为所求 ……14分
21.(Ⅰ) 解:![]() 时,f(x)>1
时,f(x)>1
令x=-1,y=0则f(-1)=f(-1)f(0)∵f(-1)>1
∴f(0)=1……………………………2′
若x>0,则f(x-x)=f(0)=f(x)f(-x)故![]()
故x∈R f(x)>0…………………………………………………4′
任取x1<x2 ![]()
![]()
故f(x)在R上减函数………………………………………..6`
(Ⅱ) 解:①![]() 由f(x)单调性
由f(x)单调性
………………………………………………………………………………8′
an+1=an+2 故{an}等差数列 ![]() ……………………………9′
……………………………9′
②![]()
![]()
![]() 是递增数列
是递增数列
………………………………………………………………………11′
当n≥2时,![]()
![]()
|
即![]()
而a>1,∴x>1
故x的取值范围(1,+∞)……………………………14′
