导数部分
1、(广东卷)函数![]() 是减函数的区间为(D)
是减函数的区间为(D)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.(全国卷Ⅰ)函数![]() ,已知
,已知![]() 在
在![]() 时取得极值,则
时取得极值,则![]() =(B)
=(B)
(A)2 (B)3 (C)4 (D)5
3. (湖北卷)在函数![]() 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于![]() 的点中,坐标为整数的点的个数是 ( D
)
的点中,坐标为整数的点的个数是 ( D
)
 A.3 B.2 C.1 D.0
A.3 B.2 C.1 D.0
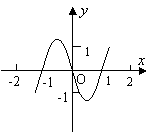
4.(江西)已知函数![]() 的图象如右图所示(其中
的图象如右图所示(其中![]() 是函数
是函数![]() 的导函数),下面四个图象中
的导函数),下面四个图象中![]() 的图象大致是(C )
的图象大致是(C )
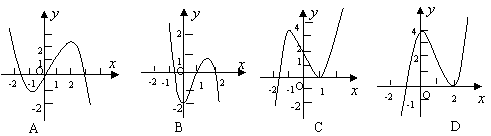

5.(浙江)函数y=ax2+1的图象与直线y=x相切,则a=( B )
(A)
![]() (B)
(B)![]() (C)
(C) ![]() (D)1
(D)1
6. (重庆卷)曲线y=x3在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为______8/3____。
7.(江苏卷)(14)曲线![]() 在点(1,3)处的切线方程是
在点(1,3)处的切线方程是![]()
8. ( 全国卷III)曲线![]() 在点(1,1)处的切线方程为x+y-2=0
在点(1,1)处的切线方程为x+y-2=0
9. (北京卷)过原点作曲线y=ex的切线,则切点的坐标为 (1, e); ,切线的斜率为e .
10.(全国卷Ⅱ)设a为实数,函数![]()
(Ⅰ)求![]() 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线![]() 轴仅有一个交点.
轴仅有一个交点.
解:(I)![]() =3
=3![]() -2
-2![]() -1
-1
若![]() =0,则
=0,则![]() ==-
==-![]() ,
,![]() =1
=1
当![]() 变化时,
变化时,![]() ,
,![]() 变化情况如下表:
变化情况如下表:
|
| (-∞,- | - | (- | 1 | (1,+∞) |
|
| + | 0 | - | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
∴![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]()
(II)函数![]()
由此可知,取足够大的正数时,有![]() >0,取足够小的负数时有
>0,取足够小的负数时有![]() <0,所以曲线
<0,所以曲线![]() =
=![]() 与
与![]() 轴至少有一个交点
轴至少有一个交点
结合![]() 的单调性可知:
的单调性可知:
当![]() 的极大值
的极大值![]() <0,即
<0,即![]() 时,它的极小值也小于0,因此曲线
时,它的极小值也小于0,因此曲线![]() =
=![]() 与
与![]() 轴仅有一个交点,它在(1,+∞)上。
轴仅有一个交点,它在(1,+∞)上。
当![]() 的极小值
的极小值![]() -1>0即
-1>0即![]()
![]() (1,+∞)时,它的极大值也大于0,因此曲线
(1,+∞)时,它的极大值也大于0,因此曲线![]() =
=![]() 与
与![]() 轴仅有一个交点,它在(-∞,-
轴仅有一个交点,它在(-∞,-![]() )上。
)上。
∴当![]() ∪(1,+∞)时,曲线
∪(1,+∞)时,曲线![]() =
=![]() 与
与![]() 轴仅有一个交点。
轴仅有一个交点。
11. (全国卷Ⅱ)已知a≥ 0 ,函数f(x) = ( ![]() -2ax )
-2ax )![]()
(1) 当X为何值时,f(x)取得最小值?证明你的结论;
(2)设 f(x)在[ -1,1]上是单调函数,求a的取值范围.
解:(I)对函数![]() 求导数得
求导数得![]()
令![]() 得[
得[![]() +2(1-
+2(1-![]() )
)![]() -2
-2![]() ]
]![]() =0从而
=0从而![]() +2(1-
+2(1-![]() )
)![]() -2
-2![]() =0
=0
解得
![]()
当![]() 变化时,
变化时,![]() 、
、![]() 的变化如下表
的变化如下表
|
| | | | | |
| | + | 0 | - | 0 | + |
|
| 递增 | 极大值 | 递减 | 极小值 | 递增 |
∴![]() 在
在![]() =
=![]() 处取得极大值,在
处取得极大值,在![]() =
=![]() 处取得极小值。
处取得极小值。
当![]() ≥0时,
≥0时,![]() <-1,
<-1,![]()
![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 上为增函数
上为增函数
而当![]() 时
时![]() =
=![]() ,当x=0时,
,当x=0时,![]()
所以当![]() 时,
时,![]() 取得最小值
取得最小值
(II)当![]() ≥0时,
≥0时,![]() 在
在![]() 上为单调函数的充要条件是
上为单调函数的充要条件是![]()
即![]() ,解得
,解得![]()
![]()
于是![]() 在[-1,1]上为单调函数的充要条件是
在[-1,1]上为单调函数的充要条件是![]()
即![]() 的取值范围是
的取值范围是![]()
12. ( 全国卷III)用长为90cm,宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边翻转90°角,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?最大容积是多少?
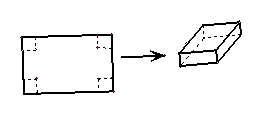 解:设容器的高为x,容器的体积为V,1分
解:设容器的高为x,容器的体积为V,1分
则V=(90-2x)(48-2x)x,(0<V<24)5分
=4x3-276x2+4320x
∵V′=12 x2-552x+4320……7分
由V′=12 x2-552x+4320=0得x1=10,x2=36
∵x<10 时,V′>0,
10<x<36时,V′<0,
x>36时,V′>0,
所以,当x=10,V有极大值V(10)=1960……………………………………………………10分
又V(0)=0,V(24)=0,…………………………………………………………………………11分
所以当x=10,V有最大值V(10)=1960………………………………………………………12分
13. ( 全国卷III)已知函数![]() ,
,![]()
(Ⅰ)求![]() 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设![]() ,函数
,函数![]() ,若对于任意
,若对于任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范围
的取值范围
解:对函数![]() 求导,得
求导,得
![]()
![]()
令![]() 解得
解得 ![]() 或
或![]()
当![]() 变化时,
变化时,![]() 、
、![]() 的变化情况如下表:
的变化情况如下表:
| x | 0 |
|
|
|
|
|
|
| 0 |
| ||
|
|
|
|
|
|
|
所以,当![]() 时,
时,![]() 是减函数;当
是减函数;当![]() 时,
时,![]() 是增函数;
是增函数;
当![]() 时,
时,![]() 的值域为
的值域为![]()
(Ⅱ)对函数![]() 求导,得
求导,得
![]()
因此![]() ,当
,当![]() 时,
时, ![]()
因此当![]() 时,
时,![]() 为减函数,从而当
为减函数,从而当![]() 时有
时有
![]()
又![]() ,
,![]() ,即当
,即当![]() 时有
时有
![]()
任给![]() ,
,![]() ,存在
,存在![]() 使得
使得![]() ,则
,则
![]()
即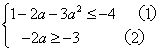
解![]() 式得
式得 ![]() 或
或![]()
解![]() 式得
式得 ![]()
又![]() ,
,
故:![]() 的取值范围为
的取值范围为![]()
14. (北京卷)已知函数f(x)=-x3+3x2+9x+a,
(I)求f(x)的单调递减区间;
(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
解:(I) f ’(x)=-3x2+6x+9.令f ‘(x)<0,解得x<-1或x>3,
所以函数f(x)的单调递减区间为(-∞,-1),(3,+∞).
(II)因为f(-2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a,
所以f(2)>f(-2).因为在(-1,3)上f ‘(x)>0,所以f(x)在[-1, 2]上单调递增,又由于f(x)在[-2,-1]上单调递减,因此f(2)和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值,于是有 22+a=20,解得 a=-2.
故f(x)=-x3+3x2+9x-2,因此f(-1)=1+3-9-2=-7,
即函数f(x)在区间[-2,2]上的最小值为-7.
15.(福建卷)已知函数![]() 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为![]() .
.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 的单调区间.
的单调区间.
解:(Ⅰ)由![]() 的图象经过P(0,2),知d=2,所以
的图象经过P(0,2),知d=2,所以![]()
![]()
由在![]() 处的切线方程是
处的切线方程是![]() ,知
,知
![]()
![]()
故所求的解析式是 ![]()
(Ⅱ)![]()
解得 ![]() 当
当![]()
当![]()
故![]() 内是增函数,在
内是增函数,在![]() 内是减函数,
内是减函数,
在![]() 内是增函数.
内是增函数.
16.(福建卷)已知函数![]() 的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
的图象在点M(-1,f(x))处的切线方程为x+2y+5=0.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
解:(1)由函数f(x)的图象在点M(-1f(-1))处的 切线方程为x+2y+5=0,知
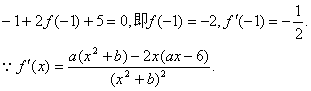

17. (湖北卷) 已知向量![]() 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
解法1:依定义![]()
![]()
![]()
![]()
![]() 开口向上的抛物线,故要使
开口向上的抛物线,故要使![]() 在区间
在区间
(-1,1)上恒成立![]()
![]()
![]()
![]() .
.
解法2:依定义![]()
![]()
![]() 的图象是开口向下的抛物线,
的图象是开口向下的抛物线,
![]()
![]()
18.(湖南卷)设![]() ,点P(
,点P(![]() ,0)是函数
,0)是函数![]() 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用![]() 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数![]() 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求![]() 的取值范围.
的取值范围.
解:(I)因为函数![]() ,
,![]() 的图象都过点(
的图象都过点(![]() ,0),所以
,0),所以![]() ,
,
即![]() .因为
.因为![]() 所以
所以![]() .
.
![]()
又因为![]() ,
,![]() 在点(
在点(![]() ,0)处有相同的切线,所以
,0)处有相同的切线,所以![]()
而![]()
将![]() 代入上式得
代入上式得![]() 因此
因此![]() 故
故![]() ,
,![]() ,
,![]()
(II)解法一![]() .
.
当![]() 时,函数
时,函数![]() 单调递减.
单调递减.
由![]() ,若
,若![]() ;若
;若![]()
由题意,函数![]() 在(-1,3)上单调递减,则
在(-1,3)上单调递减,则
![]()
所以![]()
又当![]() 时,函数
时,函数![]() 在(-1,3)上单调递减.
在(-1,3)上单调递减.
所以![]() 的取值范围为
的取值范围为![]()
解法二:![]()
因为函数![]() 在(-1,3)上单调递减,且
在(-1,3)上单调递减,且![]() 是(-1,3)
是(-1,3)
上的抛物线,
所以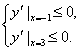 即
即![]() 解得
解得![]()
所以![]() 的取值范围为
的取值范围为![]()
19.(湖南卷)已知函数f(x)=lnx,g(x)=![]() ax2+bx,a≠0.
ax2+bx,a≠0.
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N处的切线不平行.
解:(I)![]() ,
,
则![]()
因为函数h(x)存在单调递减区间,所以![]() <0有解.
<0有解.
又因为x>0时,则ax2+2x-1>0有x>0的解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解;
则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0.
综上所述,a的取值范围为(-1,0)∪(0,+∞).
(II)证法一 设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为![]()
C1在点M处的切线斜率为![]()
C2在点N处的切线斜率为![]()
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2.
即![]() ,则
,则
![]()
=![]()
所以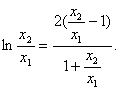 设
设![]() 则
则![]() ①
①
令![]() 则
则![]()
因为![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() )上单调递增. 故
)上单调递增. 故![]()
则![]() . 这与①矛盾,假设不成立.
. 这与①矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
证法二:同证法一得![]()
因为![]() ,所以
,所以![]()
令![]() ,得
,得![]() ②
②
令![]()
因为![]() ,所以
,所以![]() 时,
时,![]()
故![]() 在[1,+
在[1,+![]() 上单调递增.从而
上单调递增.从而![]() ,即
,即![]()
于是![]() 在[1,+
在[1,+![]() 上单调递增.
上单调递增.
故![]() 即
即![]() 这与②矛盾,假设不成立.
这与②矛盾,假设不成立.
故C1在点M处的切线与C2在点N处的切线不平行.
20.(辽宁卷)函数![]() 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数![]() 是减函数,且
是减函数,且![]() 设
设![]() 是曲线
是曲线![]() 在点(
在点(![]() )得的切线方程,并设函数
)得的切线方程,并设函数![]()
(Ⅰ)用![]() 、
、![]() 、
、![]() 表示m;
表示m;
(Ⅱ)证明:当![]() ;
;
(Ⅲ)若关于![]() 的不等式
的不等式![]() 上恒成立,其中a、b为实数,
上恒成立,其中a、b为实数,
求b的取值范围及a与b所满足的关系.
解:(Ⅰ)![]() …………………………………………2分
…………………………………………2分
(Ⅱ)证明:令![]()
因为![]() 递减,所以
递减,所以![]() 递增,因此,当
递增,因此,当![]() ;
;
当![]() .所以
.所以![]() 是
是![]() 唯一的极值点,且是极小值点,可知
唯一的极值点,且是极小值点,可知![]() 的
的
最小值为0,因此![]() 即
即![]() …………………………6分
…………………………6分
(Ⅲ)解法一:![]() ,
,![]() 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.
![]() 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
![]()
另一方面,由于![]() 满足前述题设中关于函数
满足前述题设中关于函数![]() 的条件,利用(II)的结果可知,
的条件,利用(II)的结果可知,![]() 的充要条件是:过点(0,
的充要条件是:过点(0,![]() )与曲线
)与曲线![]() 相切的直线的斜率大于
相切的直线的斜率大于![]() ,该切线的方程为
,该切线的方程为![]()
于是![]() 的充要条件是
的充要条件是![]() …………………………10分
…………………………10分
综上,不等式![]() 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
![]() ①
①
显然,存在a、b使①式成立的充要条件是:不等式![]() ②
②
有解、解不等式②得![]() ③
③
因此,③式即为b的取值范围,①式即为实数在a与b所满足的关系.…………12分
(Ⅲ)解法二:![]() 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.
![]() 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
![]() ………………………………………………………………8分
………………………………………………………………8分
令![]() ,于是
,于是![]() 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
![]() 由
由![]()
当![]() 时
时![]() 当
当![]() 时,
时,![]() ,所以,当
,所以,当![]() 时,
时,![]() 取最小值.因此
取最小值.因此![]() 成立的充要条件是
成立的充要条件是![]() ,即
,即![]() ………………10分
………………10分
综上,不等式![]() 对任意
对任意![]() 成立的充要条件是
成立的充要条件是
![]() ①
①
显然,存在a、b使①式成立的充要条件是:不等式![]() ②
②
有解、解不等式②得![]()
因此,③式即为b的取值范围,①式即为实数在a与b所满足的关系.…………12分
21. (山东卷)已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]() ,
,
(I)求![]() 与
与![]() 的关系式;
的关系式;
(II)求![]() 的单调区间;
的单调区间;
(III)当![]() 时,函数
时,函数![]() 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3![]() ,求
,求![]() 的取值范围.
的取值范围.
解(I)![]() 因为
因为![]() 是函数
是函数![]() 的一个极值点,所以
的一个极值点,所以![]() ,即
,即![]() ,所以
,所以![]()
(II)由(I)知,![]() =
=![]()
当![]() 时,有
时,有![]() ,当
,当![]() 变化时,
变化时,![]() 与
与![]() 的变化如下表:
的变化如下表:
|
|
|
|
| 1 |
|
|
|
| 0 |
| 0 |
|
|
| 调调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
故有上表知,当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
(III)由已知得![]() ,即
,即![]()
又![]() 所以
所以![]() 即
即![]() ①
①
设![]() ,其函数开口向上,由题意知①式恒成立,
,其函数开口向上,由题意知①式恒成立,
所以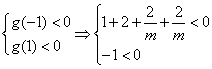 解之得
解之得![]() 又
又![]() 所以
所以![]()
即![]() 的取值范围为
的取值范围为![]()
22.(重庆卷)设函数f(x)=2x3-3(a+1)x2+6ax+8,其中aÎR。
(1) 若f(x)在x=3处取得极值,求常数a的值;
(2) 若f(x)在(-¥,0)上为增函数,求a的取值范围。
解:(Ⅰ)![]()
因![]() 取得极值, 所以
取得极值, 所以![]() 解得
解得![]()
经检验知当![]() 为极值点.
为极值点.
(Ⅱ)令![]()
当![]() 和
和![]() 上为增函数,故当
上为增函数,故当![]() 上为增函数.
上为增函数.
当![]() 上为增函数,从而
上为增函数,从而![]() 上也为增函数.
上也为增函数.
综上所述,当![]() 上为增函数.
上为增函数.
23. (重庆卷)已知aÎR,讨论函数f(x)=ex(x2+ax+a+1)的极值点的个数。
19.(本小题13分)
解:![]()
令![]() =0得
=0得![]()
(1)当![]()
即![]() <0或
<0或![]() >4时
>4时![]() 有两个不同的实根
有两个不同的实根![]() ,
,![]() ,不妨设
,不妨设![]() <
<![]()
于是![]() ,从而有下表
,从而有下表
| x |
| x1 |
|
|
|
|
| + | 0 | - | 0 | + |
|
| ↑ |
| ↓ |
| ↑ |
即此时![]() 有两个极值点.
有两个极值点.
(2)当△=0即![]() =0或
=0或![]() =4时,方程
=4时,方程![]() 有两个相同的实根
有两个相同的实根![]()
于是![]()
故当![]() <
<![]() 时
时![]() >0,当
>0,当![]() >
>![]() 时
时![]() >0,因此
>0,因此![]() 无极值
无极值
(3)当△<0即0<![]() <4时
<4时![]()
![]() ,故
,故![]() 为增函数,此时
为增函数,此时![]() 无极值. 因此当
无极值. 因此当![]() 无极值点.
无极值点.
24.(江苏卷)已知![]() 函数
函数![]()
(Ⅰ)当a=2时,求使f(x)=x成立的x的集合;
(Ⅱ)求函数y=f (x)在区间[1,2]上的最小值.
解:(1)当a=2时,![]() ,则方程f(x)=x即为
,则方程f(x)=x即为![]()
|
|
解方程得:![]()
(2)(I)当a>0时,![]()
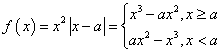 ,
,
作出其草图见右, 易知![]() 有两个极值点
有两个极值点![]() 借助于图像可知
借助于图像可知
当![]() 时,函数
时,函数![]() 在区间[1,2]上为增函数,此时
在区间[1,2]上为增函数,此时![]()
当![]() 时,显然此时函数的最小值为
时,显然此时函数的最小值为![]()
当![]() 时,
时,![]() ,此时
,此时![]() 在区间
在区间![]() 为增函数,在区间
为增函数,在区间![]() 上为减函数,∴
上为减函数,∴![]() ,又可得
,又可得![]()
∴![]()
则当![]() 时,
时,![]() ,此时
,此时![]()
|
|
当![]() 时,
时,![]() ,此时
,此时![]()
当![]() 时,
时,![]() ,此时
,此时![]() 在区间
在区间![]() 为增函数,故
为增函数,故![]()
(II)当![]() 时,
时,![]() ,此时
,此时![]() 在区间
在区间![]() 也为增函数,故
也为增函数,故![]()
(III)当![]() 时,其草图见右
时,其草图见右
显然函数![]() 在区间
在区间![]() 为增函数,故
为增函数,故![]()