2005年高考理科数学![]() 山东卷
山东卷![]() 试题及答案
试题及答案
源头学子小屋 ![]()
第Ⅰ卷(选择题 共60分)
参考公式:
如果事件A、B互斥,那么
![]()
![]()
如果事件A、B相互独立,那么 ![]() =
=![]()
![]()
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中, 只有一项是最符合题目要求的![]()
(1)![]()
(A)![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)
![]()
(2)函数![]() 的反函数的图象大致是
的反函数的图象大致是
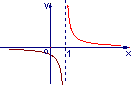
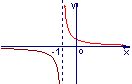
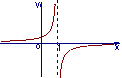
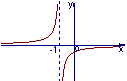
(A) (B) (C) (D)
(3)已知函数![]() 则下列判断正确的是
则下列判断正确的是
(A)此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
(B) 此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
(C) 此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
(D) 此函数的最小正周期为![]() ,其图象的一个对称中心是
,其图象的一个对称中心是![]()
(4)下列函数中既是奇函数,又是区间![]() 上单调递减的是
上单调递减的是
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
![]()
(5)如果![]() 的展开式中各项系数之和为128,则展开式中
的展开式中各项系数之和为128,则展开式中![]() 的系数是
的系数是
(A)![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)![]()
(6)函数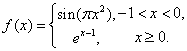 若
若![]() 则
则![]() 的所有可能值为
的所有可能值为
(A)
![]() (B)
(B) ![]() (C)
(C) ![]() ,
,![]() (D)
(D) ![]() ,
,![]()
(7)已知向量![]() ,且
,且![]() 则一定共线的
则一定共线的
(A) A、B、D (B) A、B、C (C) B、C、D (D)A、C、D
(8)设地球半径为R,若甲地位于北纬![]() 东经
东经![]() ,乙地位于南纬度
,乙地位于南纬度![]() 东经
东经![]() ,则甲、乙两地球面距离为
,则甲、乙两地球面距离为
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(9)10张奖券中只有3张有奖,5个人购买,每人1张,至少有1人中奖的概率是
(A)
![]() (B)
(B) ![]() (C)
(C)
![]() (D)
(D)![]()
(10)设集合A、B是全集U的两个子集,则![]() 是
是![]()
(A) 充分不必要条件 (B) 必要不充分条件
(C) 充要条件 (D)既不充分也不必要条件
(11)![]() 下列不等式一定成立的是
下列不等式一定成立的是
(A)![]()
(B) ![]()
(C) ![]()
(D) ![]()
(12)设直线![]() 关于原点对称的直线为
关于原点对称的直线为![]() ,若
,若![]() 与椭圆
与椭圆![]() 的交点为A、B,点P为椭圆上的动点,则使
的交点为A、B,点P为椭圆上的动点,则使![]() 的面积为
的面积为![]() 的点P的个数为
的点P的个数为
(A) 1 (B) 2 (C) 3 (D)4
第Ⅱ卷(共100分)
二、填空题:本大题共4小题,
每小题4分,共16分,把答案填在题中横线上![]()
(13)![]() __________
__________![]()
(14)设双曲线![]() 的右焦点为F,右准线
的右焦点为F,右准线![]() 与两条渐近线交于P、Q两点,如果
与两条渐近线交于P、Q两点,如果![]() 是直角三角形,则双曲线的离心率
是直角三角形,则双曲线的离心率![]()
![]()
(15)设![]() 满足约束条件
满足约束条件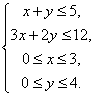 则使得目标函数
则使得目标函数![]() 的值最大的点
的值最大的点![]() 是_______
是_______![]()
(16)已知m、n是不同的直线,![]() 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题:
①若![]() 则
则![]()
![]()
②若![]() 则
则![]()
![]()
③若![]() ,则
,则![]()
![]()
④m、n是两条异面直线,若![]() 则
则![]()
![]()
上面命题中,真命题的序号是____________(写出所有真命的序号)![]()
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤![]()
(17)(本小题满分12分)
已知向量![]() 和
和![]() ,且
,且![]() ,求
,求![]() 的值
的值![]()
\
(18) (本小题满分12分)
袋中装有罴球和白球共7个,从中任取2个球都是白球的概率为![]() .现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取
.现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取![]() 取后不放回,直到两人中有一人取到白球时即终止
取后不放回,直到两人中有一人取到白球时即终止![]() 每个球在每一次被取出的机会是等可能的,用
每个球在每一次被取出的机会是等可能的,用![]() 表示取球终止时所需的取球次数.
表示取球终止时所需的取球次数.
![]() (Ⅰ)求袋中原有白球的个数;
(Ⅰ)求袋中原有白球的个数;
(Ⅱ)求随机变量![]() 的概率分布;
的概率分布;
(Ⅲ)求甲取到白球的概率![]()
(19) (本小题满分12分)
已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]()
![]() .
.
(Ⅰ)求m与n的关系表达式;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,函数
时,函数![]() 的图象上任意一点的切线斜率恒大于3m,求m的取值范围
的图象上任意一点的切线斜率恒大于3m,求m的取值范围![]()
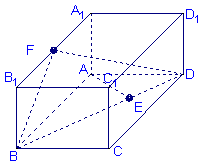 (20) (本小题满分12分)
(20) (本小题满分12分)
如图,已知长方体![]()
![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,![]() 垂直
垂直![]() 于
于![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成二面角(锐角)的大小;
所成二面角(锐角)的大小;
(Ⅲ)求点![]() 到平面
到平面![]() 的距离
的距离![]()
(21) (本小题满分12分)已知数列![]() 的首项
的首项![]() 前
前![]() 项和为
项和为![]() ,且
,且![]()
(I)证明数列![]() 是等比数列;
是等比数列;
(II)令![]() ,求函数
,求函数![]() 在点
在点![]() 处的导数
处的导数![]() 并比较
并比较![]() 与
与![]() 的大小
的大小![]()
(22) (本小题满分14分)已知动圆过定点![]() ,且与直线
,且与直线![]() 相切,其中
相切,其中![]() .
.
(I)求动圆圆心![]() 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹![]() 上异于原点
上异于原点![]() 的两个不同点,直线
的两个不同点,直线![]() 和
和![]() 的倾斜角分别为
的倾斜角分别为![]() 和
和![]() ,当
,当![]() 变化且
变化且![]() 为定值
为定值![]() 时,证明直线
时,证明直线![]() 恒过定点,并求出该定点的坐标
恒过定点,并求出该定点的坐标![]()
2005年高考理科数学![]() 山东卷
山东卷![]() 试题及答案
试题及答案
参考答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | B | B | D | C | C | A | D | D | A | A | B |
(13)![]() (14)
(14)![]() (15)
(15)![]() )
(16)③④
)
(16)③④
(17)(本小题满分12分)考查知识点:(三角和向量相结合)
解法一:
![]()
![]()
![]()
![]()
![]()
由已知![]() ,得
,得![]()
![]()
又![]()
所以 ![]()
![]()
∵ ![]()
∴ ![]()
![]()
解法二:
![]()
![]()
![]()
![]()
![]()
![]()
由已知![]() ,得
,得
![]()
∵ ![]() ,∴
,∴ ![]()
∴ ![]()
![]()
(18) (本小题满分12分)(考查知识点:概率及分布列)
解:(1)设袋中原有![]() 个白球,由题意知:
个白球,由题意知:
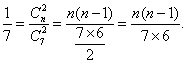
所以![]() ,解得
,解得![]() 舍去
舍去![]() ,即袋中原有3个白球
,即袋中原有3个白球![]()
(Ⅱ)由题意,![]() 的可能妈值为1,2,3,4,5.
的可能妈值为1,2,3,4,5.
![]() :
: ![]() :
: ![]()
![]() :
: ![]()
所以,取球次数![]() 的分布列为:
的分布列为:
|
| 1 | 2 | 3 | 4 | 5 |
|
|
|
|
|
|
|
(Ⅲ)因为甲先取,所以甲只有可能在第1次、第3次和第5次取球,记“甲取到白球”的事件为A,则 ![]() (“
(“![]() ”,或“
”,或“![]() ”,或“
”,或“![]() ”).
”).
因为事件“![]() ”、“
”、“![]() ”、“
”、“![]() ”两两互斥,所以
”两两互斥,所以
![]()
![]()
(19) (本小题满分12分)(考查知识点:函数结合导数)
(Ⅰ)解:![]() .
.
因为![]() 是
是![]() 的一个极值点,所以
的一个极值点,所以![]() ,即
,即![]() .
.
所以![]()
![]()
(Ⅱ)解:由(Ⅰ)知![]()
当![]() 时,有
时,有![]() ,当
,当![]() 变化时
变化时![]() 与
与![]() 的变化如下表:
的变化如下表:
|
|
|
|
| 1 |
|
|
| <0 | 0 | >0 | 0 | <0 |
|
| 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
由上表知,当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增, 在
单调递增, 在![]() 单调递减
单调递减![]()
(Ⅲ)解法一:由已知,得![]() ,即
,即![]() .
.
![]()
![]() .
.
![]()
![]() .
.
即![]() .
(*)
.
(*)
设![]() ,其函数图象的开口向上.
,其函数图象的开口向上.
由题意(*)式恒成立, ![]()
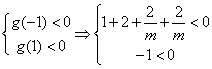
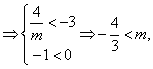 又
又![]() .
.
![]()
![]()
即![]() 的取值范围是
的取值范围是![]()
![]()
解法二:由已知,得![]() ,即
,即![]() ,
,
![]() .
. ![]() . (*)
. (*)
![]()
![]() 时. (*)式化为
时. (*)式化为![]() 怛成立.
怛成立.![]() .
.
![]()
![]() 时
时![]() .
.
(*)式化为![]() .
.
令![]() ,则
,则![]() ,记
,记![]() ,
,
则![]() 在区间
在区间![]() 是单调增函数
是单调增函数![]()
![]() .
.
由(*)式恒成立,必有![]() 又
又![]() .
.
![]() .
.
综上![]() 、
、![]() 知
知![]()
![]()
(20) (本小题满分12分)(考查知识点:立体几何)
解法一:(向量法)
在长方体![]() 中,以
中,以![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系如图.
轴建立空间直角坐标系如图.
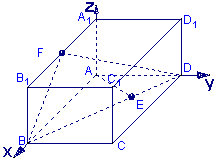 由已知
由已知![]() ,可得
,可得![]() .
.
又![]() 平面
平面![]() ,从面
,从面![]() 与平面
与平面![]() 所成的角即为
所成的角即为![]()
又![]()
![]()
从而易得![]()
![]()
(Ⅰ)![]()
![]()
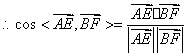
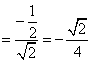
![]()
即异面直线![]() 、
、![]() 所成的角为
所成的角为![]()
![]()
(Ⅱ)易知平面![]() 的一个法向量
的一个法向量![]()
![]()
设![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.![]()
![]()
由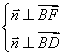
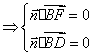
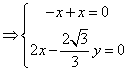
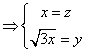
![]()
取![]()
![]()
∴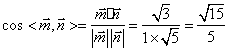
![]()
即平面![]() 与平面
与平面![]() 所成二面角(锐角)大小为
所成二面角(锐角)大小为![]()
![]()
![]()
(Ⅲ)点A到平面BDF的距离,即![]() 在平面BDF的法向量
在平面BDF的法向量![]() 上的投影的绝对值
上的投影的绝对值![]()
所以距离
![]()

![]()
![]()
所以点A到平面BDF的距离为![]()
![]()
解法二:(几何法)
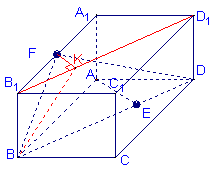 (Ⅰ)连结
(Ⅰ)连结![]() ,过F作
,过F作![]() 的垂线,垂足为K,
的垂线,垂足为K,
∵![]() 与两底面ABCD,
与两底面ABCD,![]() 都垂直,
都垂直,![]()
∴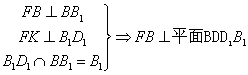
又
因此![]()
![]()
∴![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角
所成的角![]()
连结BK,由FK⊥面![]() 得
得![]() ,
,
从而 ![]() 为
为![]()
![]()
在 ![]() 和
和![]() 中,
中,
由![]() 得
得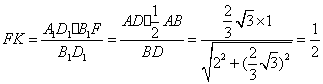
![]()
又![]() , ∴
, ∴![]()
![]()
∴异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
![]()
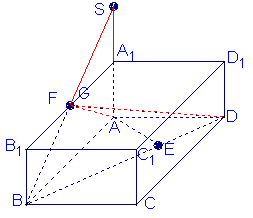 (Ⅱ)由于
(Ⅱ)由于![]() 面
面![]() 由
由![]() 作
作![]() 的垂线
的垂线![]() ,垂足
为
,垂足
为![]() ,连结
,连结![]() ,由三垂线定理知
,由三垂线定理知![]()
![]()
∴![]() 即为平面
即为平面![]() 与平面
与平面![]() 所成二面角的平面角
所成二面角的平面角![]()
且![]() ,在平面
,在平面![]() 中,延长
中,延长![]() 与
与![]() ;交于点
;交于点![]()
![]()
∵![]() 为
为![]() 的中点
的中点![]() ,
,
∴![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点
的中点![]()
即![]() ,
,
∴![]() 为等腰直角三角形,垂足
为等腰直角三角形,垂足![]() 点实为斜边
点实为斜边![]() 的中点F,即F、G重合
的中点F,即F、G重合![]()
易得![]() ,在
,在![]() 中,
中,![]()
![]()
∴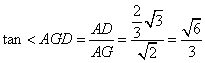 ,
,
∴![]() ,
,
即平面![]() 于平面
于平面![]() 所成二面角(锐角)的大小为
所成二面角(锐角)的大小为![]()
![]()
(Ⅲ)由(Ⅱ)知平面![]() 是平面
是平面![]() 与平面
与平面![]() 所成二面角的平面角所在的平面
所成二面角的平面角所在的平面
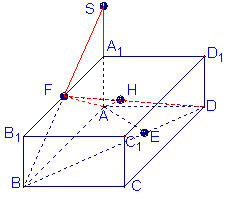 ∴面
∴面![]()
![]()
在![]() 中,由A作AH⊥DF于H,则AH即为点A到平面BDF的距离
中,由A作AH⊥DF于H,则AH即为点A到平面BDF的距离![]()
由AH![]() DF=AD
DF=AD![]() AF,得
AF,得
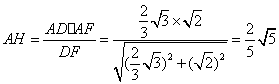
![]()
所以点A到平面BDF的距离为![]()
![]()
(21) (本小题满分12分)(考查知识点:数列)
解:由已知![]() ,
,
可得![]() 两式相减得
两式相减得
![]() 即
即![]()
从而![]()
当![]() 时
时![]() 所以
所以![]() 又
又![]() 所以
所以![]()
从而![]()
故总有![]() ,
,![]() 又
又![]()
从而![]() 即数列
即数列![]() 是等比数列;
是等比数列;
(II)由(I)知![]()
因为![]() 所以
所以![]()
从而![]() =
=![]()
=![]() -
-![]() =
=![]()
由上![]() -
-![]() =
=
![]() =12
=12![]() ①
①
当![]() 时,①式=0所以
时,①式=0所以![]() ;
;
当![]() 时,①式=-12
时,①式=-12![]() 所以
所以![]()
当![]() 时,
时,![]() 又
又![]()
![]()
![]()
所以![]() 即①
即①![]() 从而
从而![]()
![]()
![]()
(22) (本小题满分14分)(考查知识点:圆锥曲线)
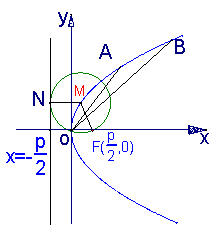 解:(I)如图,设
解:(I)如图,设![]() 为动圆圆心,
为动圆圆心,![]() 为记为
为记为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,由题意知:
,由题意知:![]() 即动点
即动点![]() 到定点
到定点![]() 与定直线
与定直线![]() 的距离相等,由抛物线的定义知,点
的距离相等,由抛物线的定义知,点![]() 的轨迹为抛物线,其中
的轨迹为抛物线,其中![]() 为焦点,
为焦点,![]() 为准线,所以轨迹方程为
为准线,所以轨迹方程为![]() ;
;
(II)如图,设![]() ,由题意得
,由题意得![]() (否则
(否则![]() )且
)且![]() 所以直线
所以直线![]() 的斜率存在,设其方程为
的斜率存在,设其方程为![]() ,显然
,显然![]() ,将
,将![]() 与
与![]() 联立消去
联立消去![]() ,得
,得![]()
由韦达定理知![]() ①
①
(1)当![]() 时,即
时,即![]() 时,
时,![]() 所以
所以![]() ,
,![]() 所以
所以![]()
由①知:![]() 所以
所以![]()
因此直线![]() 的方程可表示为
的方程可表示为![]() ,
,
即![]() 所以直线
所以直线![]() 恒过定点
恒过定点![]()
(2)当![]() 时,由
时,由![]() ,得
,得![]() =
=![]() =
=![]()
将①式代入上式整理化简可得:![]() ,所以
,所以![]() ,
,
此时,直线![]() 的方程可表示为
的方程可表示为![]()
![]() 即
即![]()
所以直线![]() 恒过定点
恒过定点![]()
![]()
所以由(1)(2)知,当![]() 时,直线
时,直线![]() 恒过定点
恒过定点![]() ,当
,当![]() 时直线
时直线![]() 恒过定点
恒过定点![]()
![]()