2006年高考理科数学摸拟试题解析样本4
本卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题共60分)
一.选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求的)
1.条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的 ( )
的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
2.设![]() 是集合A到集合B的映射,如果B={1,2},则A∩B一定是 ( )
是集合A到集合B的映射,如果B={1,2},则A∩B一定是 ( )
A.![]() B.
B.![]() 或{1} C.{1} D.
或{1} C.{1} D.![]() 或{2}
或{2}
3.过点A(-1,2)作直线,若直线在两条坐标轴上的截距相等,则满足条件的直线有( )
A.1条 B.2条 C.3条 D.4条
4.![]() 的值为 ( )
的值为 ( )
A.4 B.-4 C.2 D.-2
5.已知直线![]() 、
、![]() 与平面
与平面![]() ,给出下列四个命题
,给出下列四个命题
①若![]() ∥
∥![]() ,
,![]() b
b ![]()
![]() ,则
,则![]() ∥
∥![]() ; ②若
; ②若![]() ∥
∥![]() ,
,![]()
![]()
![]() ,则
,则![]() ∥
∥![]() ;
;
③若![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ∥
∥![]() ; ④
; ④![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,则
,则![]() ⊥
⊥![]() .
.
其中正确的命题( )
A.①和② B.①和④ C.③和④ D.只有④
6.函数![]() 的图象的相邻两支截直线
的图象的相邻两支截直线![]() 所得线段长为
所得线段长为![]() ,则
,则![]() 的值是 ( )
的值是 ( )
A.0 B.1 C.-1 D.![]()
7.(理)已知复数![]() 的辐角主值是
的辐角主值是![]() ,则
,则![]() 的辐角主值是( )
的辐角主值是( )
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
(文)定义在R上的函数![]() 的值域为[a,b],则
的值域为[a,b],则![]() 的值域为( )
的值域为( )
A.[a,b] B.[a+1,b+1]
C.[a-1,b-1] D.无法确定
8.(理)现有一块长轴长为10分米,短轴长为8分米的椭圆形玻璃镜子,欲从此镜中划出一块面积尽可能大的矩形镜子,则可划出的矩形镜子的最大面积为 ( )
A、10平方分米 B、20平方分米 C、40平方分米 D、![]() 平方分米
平方分米
(文)函数![]() 的图象 ( )
的图象 ( )
A. 关于点(-2,3)对称 B. 关于点(2,-3)对称
C. 关于直线x= -2对称 D. 关于直线y= -3对称
9.若双曲线![]() 的左支上一点P(a,b)到直线
的左支上一点P(a,b)到直线![]() 的距离为
的距离为![]() +b的值( )
+b的值( )
A.![]() B.
B.![]() C.-2 D.2
C.-2 D.2
10.已知![]() ,则向量
,则向量![]() 在向量
在向量![]() 上的投影为( )
上的投影为( )
A.![]() B.3 C.4 D.5
B.3 C.4 D.5
11.拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06(0.5·[m]+1)(元)决定,其中m>0,[m]是大于或等于m的最小整数,(如[3]=3,[3.8]=4,[3.1]=4),则从甲地到乙地通话时间为5.5分钟的电话费为 ( )
A. 3.71元 B.3.97元 C.4.24元 D. 4.77元
12.(理)在![]() 上,函数
上,函数![]() 与
与![]() 在同一点取得相同得最小值,那么
在同一点取得相同得最小值,那么![]() 在
在![]() 上的最大值是
上的最大值是
A.![]() B.4 C.8 D.
B.4 C.8 D.![]()
(文)显示屏有一排7个小孔,每个小孔可显示0或1,若每次显示其中3个孔,但相邻的两孔不能同时显示,则该显示屏能显示信号的种数共有 ( )
A.10 B.48 C.60 D.80
第Ⅱ卷(非选择题共90分)
二.填空题(本大题共4小题,每小题4分,共16分。把答案填在题中横线上)
13.已知两个命题,如果A是B的充分条件,那么B是A的______条件,如果A是B的充
分必要条件,那么![]() 的__________条件。
的__________条件。
14.关于x的方程![]() 有三个不相等的实数根,则实数a的值是 .
有三个不相等的实数根,则实数a的值是 .
15.一块用栅栏围成的长方形土地的长和宽分别为52米和24米,现欲将这块土地内部分割成一些全等的正方形试验田,要求这块土地全部被划分且分割的正方形的边与这块土地的边界平行,现另有2002米栅栏,则最多可将这块土地分割成 块。
| ξ | 0 | 1 | 2 |
| P |
|
|
|
16.设随机变量ξ的概率分布为:
则ξ的数学期望Eξ的最大值是____
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或或演算步骤)
17.(本小题满分12分)
设锐角![]() ABC中,
ABC中,![]() .
.
(1)求![]() A的大小;
A的大小;
(2)求![]() 取最大值时,
取最大值时,![]() B的大小;
B的大小;
18.(本小题满分12分)
(理)同时抛掷15枚均匀的硬币一次
(1) 试求至多有1枚正面向上的概率;
(2) 试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.
(文)已知:![]() 、
、![]() 、
、![]() 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中![]() =(1,2)
=(1,2)
(Ⅰ)若![]()
![]() ,且
,且![]() //
//![]() ,求
,求![]() 的坐标;
的坐标;
(Ⅱ)若![]() =
=![]() 且
且![]() 与
与![]() 垂直,求
垂直,求![]() 与
与![]() 的夹角θ.
的夹角θ.
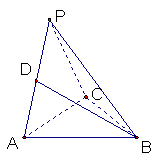
19.(本小题满分12分)
如图三棱锥P—ABC中,△ABC是正三角形,
∠PCA=90°,D为PA的中点,二面角P—AC
—B为120°,PC
= 2,AB![]() .
.
(Ⅰ)求证:AC⊥BD;
(Ⅱ)求BD与底面ABC所成角的正弦值.
20.(本小题满分12分)
(理)设函数![]() 是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,
是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,![]() (a∈R).
(a∈R).
(1)当x∈(0,1]时,求![]() 的解析式;
的解析式;
(2)若a>-1,试判断![]() 在(0,1]上的单调性,并证明你的结论;
在(0,1]上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1]时,f(x)有最大值-6.
(文)已知![]() .
.
(1)求![]() 之值;
之值;
(2)x为何值时![]() 有最小值,并求其最小值.
有最小值,并求其最小值.
21. (本小题满分12分)
一列火车自A城驶往B城,沿途有n个车站(包括起点站A和终点站B),车上有一节邮政车厢,每停靠一站便要卸下前面各站发往该站的邮袋各一个,同时又要装上该站发往后面各站的邮袋各一个,试求:
(1)列车从第k站出发时,邮政车厢内共有邮袋数是多少个?
(2)第几站的邮袋数最多?最多是多少?
22.(本小题满分14分)
已知圆![]() :
:![]() 和圆
和圆![]() :
:![]() ,现在构造一系列的圆
,现在构造一系列的圆![]() ,使圆
,使圆![]() 同时与
同时与![]() 和圆
和圆![]() 都相切,并都与OX轴相切.回答:
都相切,并都与OX轴相切.回答:
(1)求圆![]() 的半径
的半径![]() ;
;
(2)证明:两个相邻圆![]() 和
和![]() 在切点间的公切线长为
在切点间的公切线长为![]() ;
;
(3)求和![]() .
.
参考答案
一、选择题(每小题5分,满分60分)
1.A .由 条件![]() ,条件
,条件![]() ,则
,则![]() :
:![]() ,
,![]() :
:![]() ,从而仅有
,从而仅有![]()
![]()
![]() .
.
2.B .
由![]() 是集合A到集合B的映射,如果B{1,2},则A=
是集合A到集合B的映射,如果B{1,2},则A=![]() 或A=
或A=![]() 或A=
或A=![]() 或A=
或A=![]() 或A=
或A=![]() 或A=
或A=![]() 或A=
或A=![]() 或A=
或A=![]() 或A=
或A=![]() ,所以A∩B=
,所以A∩B=![]() 或{1}
或{1}
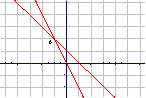 3.B . 过点A(-1,2)作直线在两条坐标轴上的截距相等,如图:
3.B . 过点A(-1,2)作直线在两条坐标轴上的截距相等,如图:
4.D. ![]() =
=![]()
=![]() =
=![]()
5.D.①错,由a∥b,b ![]() α,没有条件a
α,没有条件a ![]() α,就不能保证a∥α成立; ②错,由a∥α,b
α,就不能保证a∥α成立; ②错,由a∥α,b![]() α,推不出a∥b ;③错,由a∥α,b∥α,推不出a∥b;④正确
α,推不出a∥b ;③错,由a∥α,b∥α,推不出a∥b;④正确
6.A. 由函数![]() 的图象的相邻两支截直线
的图象的相邻两支截直线![]() 所得线段长为
所得线段长为![]() ,
,
 可得周期T=
可得周期T=![]() ,从而有
,从而有![]() 则
则![]() =
=![]()
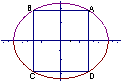 7.(理)C .如图,复数
7.(理)C .如图,复数![]() 与
与![]() 对应的向量垂直,所以
对应的向量垂直,所以![]() 的辐角主值是
的辐角主值是![]() 。
。
(文)A .当函数的图像左右平移时,不改变函数的值域。
8.(理)C.如图可设A的坐标为![]() ,
,
则有![]() =
=![]()
![]() (平方分米)
(平方分米)
(文)A. ![]() =3-
=3-![]()
9.A.由双曲线![]() 的左支上一点P(a,b)到直线(渐近线)
的左支上一点P(a,b)到直线(渐近线)![]() 的距离为
的距离为![]()
![]()
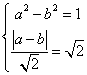 且
且![]()
![]()
![]()
10.A.由![]() 得:
得: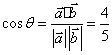 ,则向量
,则向量![]() 在向量
在向量![]() 上的投影为
上的投影为![]() 。
。
11.C.由f(m)=1.06(0.5·[m]+1)(元)得:
f(5.5)=1.06(0.5·[5.5]+1)=1.06(0.5![]() 6+1)=4.24(元)
6+1)=4.24(元)
12.(理)B. 可知![]() 在x=1时有最小值3,从而函数
在x=1时有最小值3,从而函数![]() 在x=1时有最小值3,所以p=-2,q=4,即
在x=1时有最小值3,所以p=-2,q=4,即![]() 。那么
。那么![]() 在
在![]() 上的最大值是
上的最大值是![]() 。
。
(文)D.先将要显示的3个孔插入到不要显示的4个之间或两端,有![]() 中插入方法;然后再确定每个小孔可显示的0或1,有
中插入方法;然后再确定每个小孔可显示的0或1,有![]() 种显示方法。因此能显示信号的种数共有80。
种显示方法。因此能显示信号的种数共有80。
二、填空题(每小题4分,满分16分)
13.必要条件,充要条件.
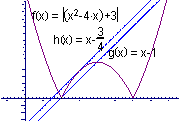 14.
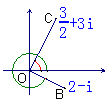
14.![]() .如图所示,要使关于x的方程
.如图所示,要使关于x的方程![]() 有三个不相等的实数根,则
有三个不相等的实数根,则![]() 与
与![]() 的图像必有三个不同的交点,所以
的图像必有三个不同的交点,所以![]() 的图像经过(1,0)或者
的图像经过(1,0)或者![]() 的图像与
的图像与![]() 的图像在[1,3]上相切。从而可得实数
的图像在[1,3]上相切。从而可得实数![]() .
.
15.设长分割成x列,宽分割成y行,共分割成z块,
则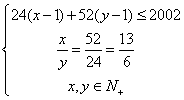
![]()
![]()
z=x·y
当x=39,y=18时,![]()
16.![]() . 由非负性
. 由非负性![]() ,Eξ=
,Eξ=![]()
三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤)
17.解:(1)∵2sin2A-cos2A=2
∴cos2A=-![]() ∴A=
∴A=![]() …………(6分)
…………(6分)
(2)y=2sin2B+sin(2B+![]() )=1+sin(2B-
)=1+sin(2B-![]() ) …………(10分)
) …………(10分)
∵0<2B<![]() ∴当2B-
∴当2B-![]() =
=![]() 即B=
即B=![]() 时,
时,![]() =2 …………(12分)
=2 …………(12分)
18.(理)解:(1)记“抛掷1枚硬币1次出现正面向上”为事件A,P(A)=![]() ,抛掷15枚硬币1次相当于作15次独立重复试验,根据几次独立重复试验中事件A发生K次的概率公式,记至多有一枚正面向上的概率为P1
,抛掷15枚硬币1次相当于作15次独立重复试验,根据几次独立重复试验中事件A发生K次的概率公式,记至多有一枚正面向上的概率为P1
则P1= P15(0)+ P15(1)=![]() +
+![]() =
=![]() ……………(6分)
……………(6分)
(2)记正面向上为奇数枚的概率为P2,则有
P2= P15(1)+ P15(3)+…+ P15(15)=![]() +
+![]() +…+
+…+![]()
=![]() +…+
+…+![]() )–
)–![]() ………………………(10分)
………………………(10分)
又“出现正面向上为奇数枚”的事件与“出现正面向上为偶数枚” 的事件是对立事件,记“出现正面向上为偶数枚” 的事件的概率为P3
![]() P3=1–
P3=1–![]() =
=![]()
![]() 相等
………………………(12分)
相等
………………………(12分)
(文)(Ⅰ)设![]()
![]() ……2分
……2分
由 ![]() ∴
∴ ![]() 或
或![]()
∴![]() ……5分
……5分
(Ⅱ)![]() ……7分
……7分
![]() ……(※)
……(※)
![]() 代入(※)中,
代入(※)中,
![]() ……10分
……10分
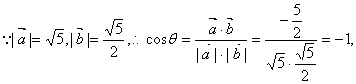
![]() ……12分
……12分
19. 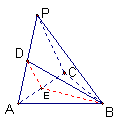 解(Ⅰ)取AC中点E,连DE、BE,则DE∥PC,PC⊥AC∴DE⊥AC ……2分
解(Ⅰ)取AC中点E,连DE、BE,则DE∥PC,PC⊥AC∴DE⊥AC ……2分
又△ABC是正三角形 ∴BE⊥AC ∴AC⊥平面DEB
又BD![]() 平面BED
平面BED
∴AC⊥BD ……5分
(Ⅱ)由(Ⅰ)中知DE⊥AC,BE⊥AC
∴∠DEB是二面角P—AC—B的平面角 ∴∠DEB=120°
又AB=![]() 其中线 BE=
其中线 BE=![]()
![]()
∵AC⊥平面BDE,AC![]() 平面ABC
平面ABC
∴平面ABC⊥平面BDE且交线为BE, ……7分
过D作平面ABC的垂线DF,垂足F必在直线BE上 又∠DEB=120°,
∴设F在BE延长线上,则∠DBE即为BD与底面ABC所成的角 ……9分
又△DEB中 ![]() ∴BD=
∴BD=![]()
由正弦定理:![]() ∴
∴![]()
即BD与底面ABC所成的角的正弦值为 ![]() ……12分
……12分
20.(本小题满分12分)
(理)(1)解:设x∈(0,1],则-x∈[-1,0),f(-x)=-2ax+![]() ,
,
∵f(x)是奇函数.
∴f(x)=2ax-![]() ,x∈(0,1]. ……3分
,x∈(0,1]. ……3分
(2)证明:∵f′(x)=2a+![]() , ……5分
, ……5分
∵a>-1,x∈(0,1],![]() >1,∴a+
>1,∴a+![]() >0.
>0.
即f′(x)>0. ……6分
∴f(x)在(0,1]上是单调递增函数. ……7分
(3)解:当a>-1时,f(x)在(0,1]上单调递增.
f(x)max=f(1)=-6,![]() a=-
a=-![]() (不合题意,舍之), ……9分
(不合题意,舍之), ……9分
当a≤-1时,f′(x)=0,x=![]() .
.
如下表:fmax(x)=f(![]() )=-6,解出a=-2
)=-6,解出a=-2![]() .
.
x=![]() ∈(0,1)
……10分
∈(0,1)
……10分
|
| (-∞, |
| ( |
|
| + | 0 | - |
| |
| 最大值 |
|
……11分
∴存在a=-2![]() ,使f(x)在(0,1]上有最大值-6. ……12分
,使f(x)在(0,1]上有最大值-6. ……12分
(文)(1)由题设知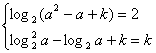
![]() ……3分
……3分
由②得![]() 或
或![]() ……4分
……4分
又![]() ≠1,故
≠1,故![]() =2 代入①
=2 代入①![]() 得
得![]() =2
……5分
=2
……5分
∴![]() =2,
=2,![]() =2
……6分
=2
……6分
(2)![]() ……8分
……8分
![]() ……10分
……10分
当![]() ……12分
……12分
21.解:设列车从各站出发时邮政车厢内的邮袋数构成一个数列![]()
(1)由题意得:
![]() …2分
…2分
在第k站出发时,前面放上的邮袋共:![]() 个 ………4分
个 ………4分
而从第二站起,每站放下的邮袋共:1+2+3+…+(k-1)个 …………6分
故![]()
![]()
即列车从第k站出发时,邮政车厢内共有邮袋数![]() 个………8分
个………8分
(2)![]()
当n为偶数时,![]() 时,最大值为
时,最大值为![]()
当n为奇数时,![]() 时,最大值为
时,最大值为![]() .………10分
.………10分
所以,当n为偶数时,第![]() 站的邮袋数最多,最多是
站的邮袋数最多,最多是![]() 个;
个;
当n为奇数时,第![]() 站的邮袋数最多,最多是
站的邮袋数最多,最多是![]() 个………12分
个………12分
22.(本小题满分14分)
解:(1)在直角梯形![]() 中,
中,
AC=1-![]() ,
,![]() =1+
=1+![]() ,
,![]() =1+
=1+![]() ,
,![]()
![]() =
=![]() +
+![]() .
.![]() =
=![]() -
-![]() .………2分
.………2分
∴有![]()
![]() ,
,![]()
![]() ,
,![]() =
=![]()
∴![]()
∴![]() .即
.即![]() .
………4分
.
………4分
由此可得![]() .
.
∴{![]() }成等差数列,
}成等差数列, ![]() .
………6分
.
………6分
∴![]() ,∴
,∴![]() .
………8分
.
………8分
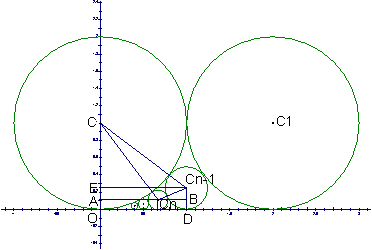
(2)公切线长为![]()
![]() . ………11分
. ………11分
(3) ![]()
![]() =
=![]() .
.
∴![]() =2.
………14分
=2.
………14分