江苏省泰兴中学2005届高考数学第三次模拟考试
本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．共150分，考试时间120分钟．
第I卷 (选择题，共60分)
注意事项：
1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2．选出答案后，用铅笔把答题卡上对应的题目的答案标号涂黑，如需改动，用橡皮擦干净后，再填涂其它答案，不能答在试卷上。
一、选择题（本题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，有且只有一个是正确的）
1、已知集合
，则集合B的非空真子集的个数为
（ ）
A、14 B、15 C、4 D、16
| 甲 | 乙 | 丙 | 丁 | |
|
| 8 | 9 | 9 | 8 |
|
| 5．7 | 6．2 | 5．7 | 6．4 |
2、甲、乙、丙、丁四名射击选手在
选拔赛中所得的平均环数
及其
方差
如下表所示，则选送
参加决赛的最佳人选是（ ）
A、甲 B、乙 C、丙 D、 丁
3、函数
（ ）
A．
B．
C．
D．
4、已知平面上直线l的方向向量e=
点O（0，0）和A（1，－2）在l上的
射影分别是O′和A′，则
e，其中
= ( )
(A)
(B)
(C)2
(D)－2
5、 已知点
,
，动点
，则点P的轨迹是（ ）
(A) 圆 (B) 椭圆 (C) 双曲线 (D) 抛物线
6、某校高三年级举行的一次演讲比赛共有10位同学参赛，其中一班有3位，二班有2位，其他班有5位. 若采取抽签的方式确定他们的演讲顺序，则一班的3位同学恰好被排在一起（指演讲序号相连），而二班的2位同学没有被排在一起的概率为（ ）
(A) 
(B)
(C)
(D)
7、命题p：若a、b∈R，则a+b>1是a+b>1的充分而不必要条件；命题q：函数
y=
的定义域是（－∞，－1
∪[3，+∞
，则 （ ）
(A)“p或q”为假 (B)“p且q”为真 (C) p真q假 (D) p假q真
8、已知
，椭圆
与双曲线
和抛物线
的离心率分别为
，则
（ ）
A、
B、
C、
D、
9、定义在
上的函数
都有反函数，又
与
的图象关于直线
对称，若
，则
（
）
A、
B、
C、
D、
10、双曲线的一条准线被它的两条渐近线所截得线段长度恰好等于它的一个焦点到一条渐近线的距离，则双曲线的离心率为 （ ）
A．3 B．2 C．
D．
11、已知数列{an}的通项公式an=log2(nÎN*),设其前n项和为Sn,则使Sn<－5成立的自然数n （ ）
A．有最小值63 B．有最大值63 C．有最小值31 D．有最大值31
12、某中学拟于下学年在高一年级开设《矩阵与变换》、《信息安全与密码》、《开关电路与布尔代数》等三门数学选修课程。在计划任教高一的10名数学教师中，有3人只能任教《矩阵与变换》，有2人只能任教《信息安全与密码》，另有3人只能任教《开关电路与布尔代数》，这三门课都能任教的只有2人。现要从这10名教师中选出9人，分别担任这三门选修课程的任课教师，且每门课程安排3名教师任教，则不同的安排方案共有：（ ）
A．
种 B．
种 C．
种 D．
种
第Ⅱ卷 (非选择题，共90分)
注意事项：
1．第Ⅱ共6页，用蓝、黑色的钢笔或圆珠笔直接答在试卷中。
2．答卷前，请将密封线内的项目填写清楚。
| 题号 | 二 | 三 | 总分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | |||
| 分数 | ||||||||
二、填空题：（本大题共4小题，每小题4分，共16分）
13、
则
的值为
14、平面上点A,B,C满足
= .
15、已知
，奇函数
在
上单调．
则字母
应满足的条件是------------------------。
16、设集合
，映射
满足
，则这种映射数为
（用数字作答）
三、解答题
17、（本小题12分）在△ABC中，三内角A、B、C所对的边分别为a、b、c。若满足
，求A、B、C的值。
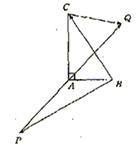18、（本小题12分） 如图，在Rt△ABC中，BC=a，若长为
2a的线段PQ以点A为中点，问
与
的值最大？
并求出这个最大值.
19、（本小题12分）在斜三棱柱A1B1C1—ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC.
(1)若D是BC的中点，求证：AD⊥CC1；
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M，若AM=MA1，求证：截面MBC1⊥侧面BB1C1C；
(3)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗？请你叙述判断理由.
20、（本小题12分）已知函数
.
（1）若
的单调减区间为（0，4），求
的值；
（2）当
时，求证
.
21．（本小题满分12分）
|
，经过其右焦点F且以
为方向向量的直线
交椭圆C于A、B两点，M为线段AB的中点，设O为椭圆的中心，射线OM交椭圆C于N点．
（I）证明：
；
（II）求
的值．
22、（本小题14分）已知等差数列
的首项为a，公差为b；等比数列
的首项为b，公比为a，其中a，
，且
．
（I）求a的值；
（II）若对于任意
，总存在
，使
，求b的值；
（III）在（II）中，记
是所有中满足， 的项从小到大依次组成的数列，又记
为的前n项和，
为的前n项和，
求证：≥
．
江苏省泰兴中学2005届高考数学第三次模拟考试
参考答案
一、选择题
1、A 2、C 3、D 4、D 5、D 6、B
7、D 8、C 9、D 10、B 11、A 12、D
二、填空题
13、2 14、-25 15、
16、4320
三、解答题
17、解：由题知：
由正弦定理，有
………………2分
余切化弦有：
………………4分
通分后，
，又
………………6分
………………8分
展开化简得：
………………10分
又
………………11分
综上：
………………12分
18、解法一：向量的矢量运算
A为PQ的中点, 
=0+(
)
-a2=
- a2= -a2cosθ- a2
故当θ=0°时最大,最大值为0.
解法二：向量的坐标运算
以A为坐标原点以AB为x轴建立直角坐标系，则B（b,0）,C(0,c),b2+c2=a2
设P(x,y)则Q点(-x,-y),x2+y2=a2
,
=-x2-y2+bx-cy=
-a2=a2cosθ-a2
下同前.
19、(1)证明：∵AB=AC，D是BC的中点，∴AD⊥BC
∵底面ABC⊥平面BB1C1C，∴AD⊥侧面BB1C1C ∴AD⊥CC1.
(2)证明：延长B1A1与BM交于N，连结C1N
∵AM=MA1，∴NA1=A1B1
∵A1B1=A1C1，∴A1C1=A1N=A1B1 ∴C1N⊥C1B1
∵底面NB1C1⊥侧面BB1C1C，∴C1N⊥侧面BB1C1C
∴截面C1NB⊥侧面BB1C1C
∴截面MBC1⊥侧面BB1C1C.
(3)解：结论是肯定的，充分性已由(2)证明，下面证必要性.
过M作ME⊥BC1于E，∵截面MBC1⊥侧面BB1C1C
∴ME⊥侧面BB1C1C，又∵AD⊥侧面BB1C1C.
∴ME∥AD，∴M、E、D、A共面
∵AM∥侧面BB1C1C，∴AM∥DE
∵CC1⊥AM，∴DE∥CC1∵D是BC的中点，∴E是BC1的中点
∴AM=DE=
AA1，∴AM=MA1.
20、【解】（1）
的解集为（0，4），0、4是3kx2-6(k+1)x=o的两根，
所以
（2）要证
，只要证
令
，
则当
时，
上递增，
即
成立，原不等式得证.
1．
（1）∵
，
, ∴
, ∴
.
∵直线过焦点且与向量平行,
∴直线的方程为：
.
3分
将其代入椭圆C的方程，并整理可得：
…①
设
，
，
，
.
∵M是线段AB的中点，在方程①中由韦达定理,可得：
, 
, ∴
.
设
为OM延长线上的点，且M为O的中点，则
，且四边形OAB为平行四边形. 将的坐标代入椭圆C方程的左端并化简得
,
∴点在椭圆C上,与N点重合,
∴四边形OANB为平行四边形于是 
． 6分
（2）
．
在方程①中由韦达定理，得 
， 9分
∴
，
∴
．
12分
22．（1）∵ 
，a，
，
∴ 
∴ 
∴ 
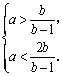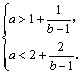2分
∴ 
． ∴ a＝2或a＝3（a＝3时不合题意，舍去）．故 a＝2． 4分
（2）
，
，由，可得
，
即 
， ∴b＝5．
8分
（3）由（2）知
，
，
∴ 
， ∴ 
，
∴ 
，
．
10分
∵ 
，
．
12分
当n≥3时，
．
∴ 
．综合以上，便得 
．
14分