长郡中学2006届高考冲刺模拟试卷(一)文科
一、选择题(每小题5分,10小题,共50分)
1、已知函数![]() ,则集合
,则集合![]()
![]() 中含有元素的个数为( )
中含有元素的个数为( )
A、0 B、1或0 C、1 D、1或2
2、已知函数![]() ,则( )
,则( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
3、设P=![]() ,Q=
,Q=![]() },已知Q∩P只有一个子集,那么实数k的取值范围是( )
},已知Q∩P只有一个子集,那么实数k的取值范围是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知函数![]() 的图象过点(1,0),则
的图象过点(1,0),则![]() 的反函数的图象一定过点( )
的反函数的图象一定过点( )
A、(0,2) B、(2,0) C、(2,1) D、(1,2)
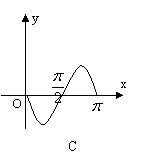
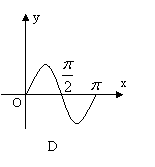
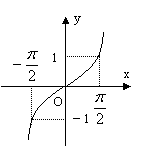 5、已知
5、已知![]() 的图象如右图所示,则
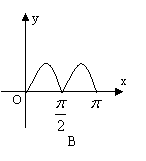
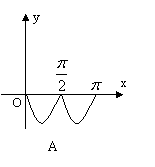
的图象如右图所示,则![]() 在区间[0,
在区间[0,![]() ]上大致图象是( )
]上大致图象是( )
 | |||
 | |||
 | |||
 | |||
6、设F1和F2为双曲线![]() 的两个焦点,点P在双曲线上,若
的两个焦点,点P在双曲线上,若![]() ,则△F1PF2的面积是( )
,则△F1PF2的面积是( )
A、1 B、![]() C、2 D、
C、2 D、![]()
7、![]() 被8除所得余数是( )
被8除所得余数是( )
A、0 B、2 C、3 D、5
8、某省举行的一次民歌大奖赛中,全省六个地区各送了一对歌手参赛,现从这12名选手中选出4名优胜者,则选出的4名优胜者中,恰有两人是同一地区来的歌手的概率是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、设![]() ,则二次曲线
,则二次曲线![]() 与
与![]() 必有( )
必有( )
A、不同的顶点 B、不同的准线
C、相同的焦点 D、相同的离心率
10、若三棱锥的顶点S在底面上的射影H恰好是底面三角形的三条高的交点,则三棱锥必有( )
A、三条侧棱长相等 B、三个侧面与底在所成的二面角相等
C、三条侧棱分别与它相对的棱垂直 D、一定是正三棱锥
长郡中学2006届高考冲刺模拟试卷(一)文科答卷
一、选择题(每小题5分,10小题,共50分)
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(每小题4分,5小题,共20分)
11、若函数![]() ,则函数
,则函数![]() 的最大值
,最小值
。
的最大值
,最小值
。
12、![]() (x>1,p为正常数),
(x>1,p为正常数),![]() 有相同值域,则P的值为
。
有相同值域,则P的值为
。
13、对一个容量为20的样本数据分为三组,第一组的频率为25%,后两组的频率之比为4:1,那么在这三组数据中,频率最小的一组的频数为
14、与圆![]() 切于点
切于点![]() (3,6),且过点
(3,6),且过点![]() (5,6)的圆的方程是
(5,6)的圆的方程是
___________________.
15、已知命题:“若数列![]() 为等差数列,且
为等差数列,且![]() ,则
,则![]() ”,现已知数列
”,现已知数列![]()
![]() 为等比数列,且
为等比数列,且![]()
![]() ,若类比上述结论,则可得
,若类比上述结论,则可得![]() 。
。
三、解答题(6小题,共80分)
16、在△ABC中,角A,B,C的对边的边长分别为a,b,c,若![]() ,且
,且![]() ,试求
,试求![]() 的值。(12分)
的值。(12分)
17、设全集![]() ,函数
,函数![]() 的定义域为A,集合
的定义域为A,集合![]() ,若
,若![]() 恰好有2个元素,求a的取值集合。(12分)
恰好有2个元素,求a的取值集合。(12分)
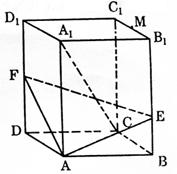
18、在长方体ABCD—A1B1C1D1中,E、F分别在BB1,DD1上,且AE⊥A1B,AF⊥A1D.
(1)求证:A1C⊥平面AEF;
(2)若AB=3,AD=4,AA1=5,M是B1C1的中点,求AM与平面AEF所成角的大小;
(3)在(2)的条件下,求三棱锥D—AEF的体积。(14分)
|
19、设![]() 为定点,P,M,N为动点,且P、M分别在y轴和x轴上,若
为定点,P,M,N为动点,且P、M分别在y轴和x轴上,若![]() 。
。
(1)求点A的轨迹C的方程。
(2)过F作直线交抛物线于A、B两点,且![]() ,求直线AB的方程。(14分)
,求直线AB的方程。(14分)
20、下面玩掷骰子放球游戏,若掷出1点,甲盒中放一球,若掷出2点或3点,乙盒中放一球,若掷出4点、5点或6点,丙盒中放一球,设掷n次后,甲、乙、丙各盒内的球数分别为![]() 。(14分)
。(14分)
(1)n=3时,求![]() 成等差数列的概率。
成等差数列的概率。
(2)当n=6时,求![]() 成等比数列的概率。
成等比数列的概率。
21、已知数列{an}中![]() 数列
数列![]() 。(14分)
。(14分)
(1)求证数列{bn}是等差数列;
(2)求数列{an}中的最大项与最小项,并说明理由;
长郡中学2006届高考冲刺模拟试卷(一)文科
参考答案
一、选择题
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | A | D | D | A | D | C | C | C |
二、填空题
11、5;-4; 12、![]() ; 13、3; 14、
; 13、3; 14、![]() ;
;
15、![]() ;
;
三、解答题
16、![]()
17、解:![]()
![]() 时,
时,![]() ∴
∴![]()
∴![]()
![]() ,∴
,∴![]()
∴![]()
当![]() 时,
时,![]() 在此区间上恰有2个偶数。
在此区间上恰有2个偶数。
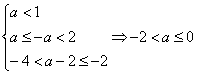
18、解:(1)∵BC⊥面A1B ∴A1C在面A1B上的射影为A1B
由A1B⊥AE AE![]() 面A1B,得A1C⊥AE,同理A1C⊥AF,
面A1B,得A1C⊥AE,同理A1C⊥AF,
∴A1C⊥面AEF.
(2)以C为原点,射线CD、CB、CC1分别为x轴、y轴、z轴的正半轴,建立空间直角坐标系,则C(0,0,0),A(3,4,0),A1(3,4,5),M(0,2,5).
∴![]() =(-3,-4,-5),
=(-3,-4,-5),![]() =(-3,-2,5)
=(-3,-2,5)
设![]() 与
与![]() 的夹角为θ,则
的夹角为θ,则
cos![]() =
=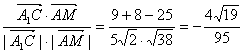
∴AM与平面AEF所成的角大小为arcsin![]() .
.
(3)∵△A1AD∽△ADF
19、解(1),设![]()
则![]() ,
,![]() ,
,![]() ,由
,由![]() ,得
,得![]() ①,由
①,由![]() 得
得![]()
![]() ∴
∴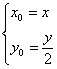 ,代入①得,
,代入①得,![]()
(2)![]()
20、解:(1)∵![]()
①![]() ②
②![]() ③
③![]()
①表示:掷3次,1次出现2点或3点,2次出现4点,5点或6点,共![]() 种情况。
种情况。
故![]() 的概率为
的概率为![]()
②![]() 的概率为
的概率为![]()
③![]() 的概率为
的概率为
![]()
故n=3时,x、y、z成等差数列,概率为![]()
(2)n=6时,x、y、z成等比数列。
∴![]()
所求概率为![]()
19、解:(1)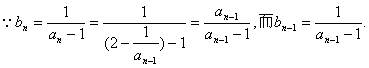
![]()
![]() ∴{bn}是首项为
∴{bn}是首项为![]() ,公差d=1的等差数列
,公差d=1的等差数列
(2)由(1)得![]()
设函数![]()
∴在区间![]() 内f(x)为减函数
内f(x)为减函数
∴当x≤3时,f(x)≥f(3)=-1 当x≥4时,f(x)≤f(4)=3。
∴an的最小值为a3=-1,最大值为a4=3
另解:an=1+![]() .
.
当n≤3时,![]() =a1>a2>a3=-1, 当n≥4时,3=a4>a5>a6>…>an>1.
=a1>a2>a3=-1, 当n≥4时,3=a4>a5>a6>…>an>1.
∴an的最小值为a3=-1,最大值为a4=3.