新教材高考数学模拟题精编详解第七套试题
| 题号 | 一 | 二 | 三 | 总分 | ||||||||
| 1～12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | ||
| 分数 | ||||||||||||
说明：本套试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分．考试时间：120分钟．
第Ⅰ卷（选择题，共60分）
一、本题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个选项是符合题目要求的．
1．（文）已知命题甲为x＞0；命题乙为
，那么（ ）
A．甲是乙的充分非必要条件
B．甲是乙的必要非充分条件
C．甲是乙的充要条件
D．甲既不是乙的充分条件，也不是乙的必要条件
（理）已知两条直线
∶ax＋by＋c＝0，直线
∶mx＋ny＋p＝0，则an＝bm是直线
的（ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
2．（文）下列函数中，周期为
的奇函数是（ ）
A．
B．
C．
D．
（理）方程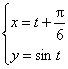
（t是参数，
）表示的曲线的对称轴的方程是（ ）
A．
B．
C．
D．
3．在复平面中，已知点A（2，1），B（0，2），C（-2，1），O（0，0）．给出下面的结论：
①直线OC与直线BA平行；
②
；
③
；
④
．
其中正确结论的个数是（ ）
A．1个 B．2个 C．3个 D．4个
4．（文）在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1∶3，则锥体被截面所分成的两部分的体积之比为（ ）
A．1∶
B．1∶9 C．1∶
D．1∶
（理）已知数列
的通项公式是
，其中a、b均为正常数，那么
与
的大小关系是（ ）
A．
B．
C．
D．与n的取值相关
5．（文）将4张互不相同的彩色照片与3张互不相同的黑白照片排成一排，任何两张黑白照片都不相邻的不同排法的种数是（ ）
A．
B．
C．
D．
（理）某农贸市场出售西红柿，当价格上涨时，供给量相应增加，而需求量相应减少，具体调查结果如下表：
表1 市场供给量
| 单价 （元/kg） | 2 | 2.4 | 2.8 | 3.2 | 3.6 | 4 |
| 供给量 （1000kg） | 50 | 60 | 70 | 75 | 80 | 90 |
表2 市场需求量
| 单价 （元/kg） | 4 | 3.4 | 2.9 | 2.6 | 2.3 | 2 |
| 需求量 （1000kg） | 50 | 60 | 65 | 70 | 75 | 80 |
根据以上提供的信息，市场供需平衡点（即供给量和需求量相等时的单价）应在区间（ ）
A.（2.3，2.6）内 B．（2.4，2.6）内
C．（2.6，2.8）内 D．（2.8，2.9）内
6．椭圆
的焦点在y轴上，长轴长是短轴长的两倍，则m的值为（ ）
A．
B．
C．2 D．4
7．若曲线
在点P处的切线平行于直线3x-y＝0，则点P的坐标为（ ）
A．（1，3） B．（-1，3）
C．（1，0） D．（-1，0）
8．已知函数
是R上的偶函数，且在（-∞，
上是减函数，若
，则实数a的取值范围是（ ）
A．a≤2 B．a≤-2或a≥2
C．a≥-2 D．-2≤a≤2
9．如图，E、F分别是三棱锥P-ABC的棱AP、BC的中点，PC＝10，AB＝6，EF＝7，则异面直线AB与PC所成的角为（ ）
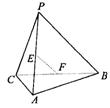
A．60° B．45° C．0° D．120°
10．圆心在抛物线
上，并且与抛物线的准线及x轴都相切的圆的方程是（ ）
A．
B．
C．
D．
11．双曲线的虚轴长为4，离心率
，
、
分别是它的左、右焦点，若过的直线与双曲线的右支交于A、B两点，且
是
的等差中项，则等于（ ）
A．
B．
C．
D．8．
12．如图，在正方形ABCD中，E、F、G、H是各边中点，O是正方形中心，在A、E、B、F、C、G、D、H、O这九个点中，以其中三个点为顶点作三角形，在这些三角形中，互不全等的三角形共有（ ）
A．6个 B．7个 C．8个 D．9个
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 得分 |
| 答案 |
第Ⅱ卷（非选择题，共90分）
二、填空题：本题共4小题，共16分，把答案填在题中的横线上
13．若
是数列的前n项的和，
，则
________．
14．若x、y满足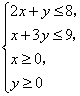
则
的最大值为________．
15．有A、B、C、D、E五名学生参加网页设计竞赛，决出了第一到第五的名次，A、B两位同学去问成绩，教师对A说：“你没能得第一名”．又对B说：“你得了第三名”．从这个问题分析，这五人的名次排列共有________种可能（用数字作答）．
16．若对n个向量
，…，
存在n个不全为零的实数
，
，…，
，使得
成立，则称向量
，
，…，为“线性相关”．依此规定，能说明
（1，2），
（1，-1），
（2，2）“线性相关”的实数，，
依次可以取________（写出一组数值即中，不必考虑所有情况）．
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤．
17．（12分）已知
，求
的值．
18．（12分）已知等比数列的公比为q，前n项的和为，且
，
，
成等差数列．
（1）求
的值；
（2）求证：
，
，
成等差数列．
19．（12分）一个口袋中装有大小相同的2个白球和3个黑球．
（1）从中摸出两个球，求两球恰好颜色不同的概率；
（2）从中摸出一个球，放回后再摸出一个球，求两球恰好颜色不同的概率．
注意：考生在（20甲）、（20乙）两题中选一题作答，如果两题都答，只以（19甲）计分．
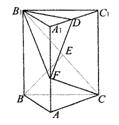
20甲．（12分）如图，正三棱柱
的底面边长为a，点M在边BC上，△
是以点M为直角顶点的等腰直角三角形．
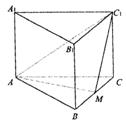
（1）求证点M为边BC的中点；
（2）求点C到平面的距离；
（3）求二面角
的大小．
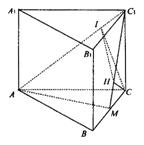
20乙．（12分）如图，直三棱柱中，底面是以∠ABC为直角的等腰直角三角形，AC＝2a，
＝3a，D为
的中点，E为
的中点．
（1）求直线BE与
所成的角；
（2）在线段
上是否存在点F，使CF⊥平面
，若存在，求出
；若不存在，说明理由．
21．（12分）已知双曲线C：
（a＞0，b＞0），B是右顶点，F是右焦点，点A在x轴正半轴上，且满足
、
、
成等比数列，过F作双曲线C在第一、第三象限的渐近线的垂线l，垂足为P．
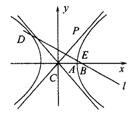
（1）求证：
；
（2）若l与双曲线C的左、右两支分别相交于点D、E，求双曲线C的离心率e的取值范围．
22．（14分）设函数
，
，且方程
有实根．
（1）证明：-3＜c≤-1且b≥0；
（2）若m是方程的一个实根，判断
的正负并加以证明．
参考答案
1．（文）A（理）C 2．（文）A（理）B 3．C 4．（文）D（理）B
5．（文）D （理）C 6．A 7．C 8．B 9．A 10．D 11．A 12．C
13．33 14．7 15．18
16．只要写出-4c，2c，c（c≠0）中一组即可，如-4，2，1等
17．解析：
．
18．解析：（1）由，，成等差数列，得
，
若q＝1，则
，
，
由
≠0 得 
，与题意不符，所以q≠1．
由
，得
．
整理，得
，由q≠0，1，得
．
（2）由（1）知：
，
，所以，，成等差数列．
19．解析：（1）记“摸出两个球，两球恰好颜色不同”为A，摸出两个球共有方法
种，
其中，两球一白一黑有
种．
∴ 
．
（2）法一：记摸出一球，放回后再摸出一个球“两球恰好颜色不同”为B，摸出一球得白球的概率为
，摸出一球得黑球的概率为
，
∴ P（B）＝0.4×0.6＋0.6＋×0.4＝0.48
法二：“有放回摸两次，颜色不同”指“先白再黑”或“先黑再白”．
∴ 
∴ “有放回摸两次，颜色不同”的概率为
．
20．解析：（甲）（1）∵ △为以点M为直角顶点的等腰直角三角形，∴ 
且
．
∵ 正三棱柱， ∴ 
底面ABC．
∴ 
在底面内的射影为CM，AM⊥CM．
∵ 底面ABC为边长为a的正三角形， ∴ 点M为BC边的中点．
（2）过点C作CH⊥
，由（1）知AM⊥且AM⊥CM，
∴ AM⊥平面
∵ CH在平面内， ∴ CH⊥AM，
∴ CH⊥平面
，由（1）知，
，
且
．
∴ 
． ∴ 
．
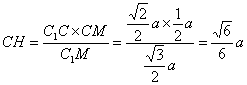∴ 点C到平面的距离为底面边长为
．
（3）过点C作CI⊥
于I，连HI， ∵ CH⊥平面，
∴ HI为CI在平面内的射影，
∴ HI⊥，∠CIH是二面角的平面角．
在直角三角形
中，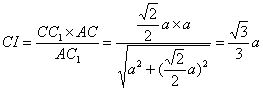
，
，
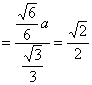∴ ∠CIH＝45°， ∴ 二面角的大小为45°
（乙）解：（1）以B为原点，建立如图所示的空间直角坐标系．
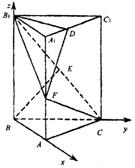
∵ AC＝2a，∠ABC＝90°，
∴ 
．
∴ B（0，0，0），C（0，
，0），A（，0，0），
（，0，3a），
（0，，3a），
（0，0，3a）．
∴ 
，
，
，
，，
，
∴ 
，
，，
，，
．
∴ 
，
， ∴ 
，
∴ 
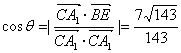． 故BE与所成的角为
．
（2）假设存在点F，要使CF⊥平面，只要
且
．
不妨设AF＝b，则F（
，0，b），
，，
，
，0，
，
，，
， ∵ 
， ∴ 恒成立．
或
，
故当
或2a时，
平面．
21．解析：（1）法一：l：
，
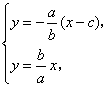
解得
，
． ∵ 、、成等比数列，
∴ 
， ∴ 
，
，，
，，
∴ 
，
． ∴
法二：同上得，．
∴ PA⊥x轴．
． ∴ ．
（2）
∴ 
．
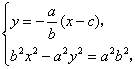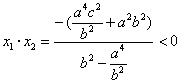即 
， ∵ 
，
∴ 
，即 
，
． ∴ 
，即 
．
22．解析：（1）
． 又c＜b＜1，
故
方程f（x）＋1＝0有实根，
即
有实根，故△＝
即
或
又c＜b＜1，得-3＜c≤-1，由
知
．
（2）
，
．
∴ c＜m＜1 ∴ 
．
∴ 
． ∴ 的符号为正．