常州第四中学2005年高考数学模拟试卷
命题人:常州市第四中学 颜瑞生
一.选择题:(5*12)
1.设集合![]() ,
,![]() 则( )
则( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
2.已知等差数列![]() 的公差为2,若
的公差为2,若![]() 成等比数列, 则
成等比数列, 则![]() = ( )
= ( )
(A) –4 (B) –6 (C) –8 (D) –10
3.在P(1,1)、Q(1,2)、M(2,3)和N![]() 四点中,函数
四点中,函数![]() 的图象与其反函数的图象的公共点只可能是点 ( )
的图象与其反函数的图象的公共点只可能是点 ( )
A.P. B.Q. C.M. D.N.
4.已知![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
5.若函数![]() 的图象过两点(-1,0)和(0,1),则 ( )
的图象过两点(-1,0)和(0,1),则 ( )
A.a=2,b=2 B.a=,b=2 C.a=2,b=1 D.a=,b=
6.把函数y=cos2x+3的图像沿向量![]() 平移后,得到函数y=sin(2x+
平移后,得到函数y=sin(2x+![]() )的图像,则向量
)的图像,则向量![]() 的坐标是
的坐标是
A(-![]() ,-3) B(
,-3) B(![]() ,3) C(-
,3) C(-![]() ,3) D(
,3) D(![]() ,-3)
,-3)
7..球面上有三点,其中任意两点的球面距离都等于球的大圆周长的六分之一,经过这三点的小圆的周长为4π,则这个球的表面积为
A12π B24π C48π D64π
8.计算机将信息转换成二进制进行处理,二进制即“逢二进一”,如(1101)2就表示一个二进制数,将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数![]() 转换成十进制形式是
转换成十进制形式是
A217-2 B218-2 C218-1 D217-1
9.过点M(1,2)的直线l将圆(x-2)2+y2=9分成两段弧,当其中的劣弧最短时,直线l的方程是
A x=1 B y=1 C x-y+1=0 D x-2y+3=0
.10.设函数![]() ,那么函数f(x+1)的图像关于直线y=x对称图像的函数的解析式是
,那么函数f(x+1)的图像关于直线y=x对称图像的函数的解析式是
A ![]() B
B ![]() C
C ![]() D
D ![]()
11.已知A箱内有红球1个和白球(n+1)个,B箱内有白球(n-1)个(n∈N,且n≥2),现随意从A箱中取出3个球放入B箱,将B箱中的球充分搅匀后,再从中随意取出3个球放入A箱,则红球由A箱移到B箱,再返回到A箱的概率等于
A![]() B
B![]() C
C![]() D
D![]()
12.对于二项式(![]() +x3)n(n∈N+),四位同学作出了四种判断:
+x3)n(n∈N+),四位同学作出了四种判断:
①存在n∈N+,展开式中有常数项;
②对任意n∈N+,展开式中没有常数项;
③对任意n∈N+,展开式中没有x的一次项;
④存在n∈N+,展开式中有x的一次项。
上述判断中正确的是
A①与③ B②与③ C②与④ D④与①
二.填空题(4*4)
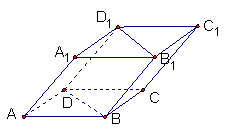
13.如图,四棱柱ABCD—A1B1C1D1的底面ABCD为正方形,侧棱与底面边长均为2a,且![]() ,则侧棱AA1和截面B1D1DB的距离是 .
,则侧棱AA1和截面B1D1DB的距离是 .
14.由动点P向圆x2+y2=1引两条切线PA、PB,切点分别为A、B,∠APB=60°,则动点P的轨迹方程为 .
15.在△ABC中,边AB为最长边,且sinA·sinB=![]() ,则cosA·cosB的最大值是
。
,则cosA·cosB的最大值是
。
16.一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于n2,则算过关,那么,连过前二关的概率是。_______。
三、解答题:
17.(本题满分12分)已知,α是锐角,且tan![]()
![]() (2)
(2)![]() 的值
的值
18.(本题满分12分)已知向量
![]()
(I)求向量![]()
(II)若映射![]()
①求映射f下(1,2)原象;
②若将(x、y)作点的坐标,问是否存在直线l使得直线l上任一点在映射f的作用下,仍在直线上,若存在求出l的方程,若不存在说明理由
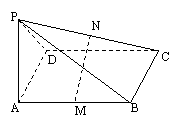 19.(本题满分12分)如图,PA⊥矩形ABCD所在平面,PA=AD=a,M,N分别是AB,PC的中点,(1)求证:MN⊥平面PCD
19.(本题满分12分)如图,PA⊥矩形ABCD所在平面,PA=AD=a,M,N分别是AB,PC的中点,(1)求证:MN⊥平面PCD
(2)若AB=![]()
20.(本题满分12分)求
![]()
21. (本题满分12分)(1)设
M(![]() 互相垂直的弦MP、MQ,求证:PQ恒过定点M'(
互相垂直的弦MP、MQ,求证:PQ恒过定点M'(![]()
(2)直线![]() 点M,使得△MPQ为以PQ为斜边的直角三角形?
点M,使得△MPQ为以PQ为斜边的直角三角形?
22.(本题满分14分)数列![]()
(1)若数列![]()
(2)求数列![]() 的通项公式
的通项公式![]()
(3)数列![]() 适合条件的项;若不存在,请说明理由
适合条件的项;若不存在,请说明理由
参考答案
选择题BBDCADDCDBCD
13.a
14.![]() ,15. 16.
,15. 16.![]()
17.解:(1)![]()
由![]() =2,有
=2,有![]() =2
=2
解得![]()
(2)原式=![]()
![]()
![]()
18.解:(I)设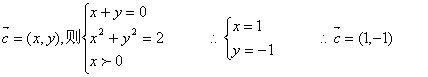
(II)①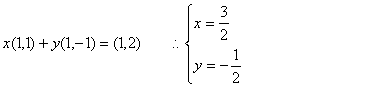
![]()
②假设l存在,设其方程为![]()
![]()
点![]()
![]()
即(1+k)![]()
![]()
![]()
19.(1)证明:取PD中点E,∵E,N分别是PD,PC中点,
∴ ![]()
![]() ∥MN
∥MN
∵PA=AD ∴AE⊥PD
又∵PA⊥平面ABCD ∴PA⊥CD,CD⊥AD
PA∩AD=A ∴CD⊥平面PAD
AE平面PAD ∴AE⊥CD,CD∩PD=D
∴AE⊥平面PCD ∴MN⊥平面PCD
(2)解:连AC交BD于O,则O是AC中点,连ON则ON⊥ABCD
作OF⊥MD,连NF,则NF⊥MD
∴∠NFO是二面角N—DM——C的平面角,
NO=![]()
![]() ∠NFO=
∠NFO=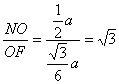
二面角N—MD——C为60°
20.解:![]()
![]()
又![]()
![]()
![]() )
)
![]()
![]()
![]()
![]()
=![]()
![]()
所以,最大值只可能是![]()
再比较![]()
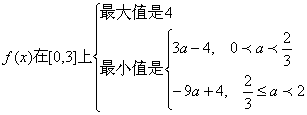
最大值是![]()
最小值只能是![]()
故当![]()
![]()
在[0,3]的最小值是![]()
当![]() 时,
时,![]()
21.(1)证明:设PQ的方程为![]()
得 ![]()
![]() 其中
其中![]()
![]()
即![]() ∴
∴![]()
![]()
![]()
直线PQ的方程为![]()
即![]()
(2)设M(![]() 上,所以
上,所以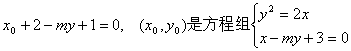 的解,消去x得
的解,消去x得
![]()
![]() 。
。
22.解:(1)由![]()
∴![]()
(2)![]()
![]()
(3)设存在S,P,r![]()
![]()
即 ![]()
![]()
![]() 为偶数
为偶数
1+2![]()