2004-2005届高考数学仿真试题(二)(广东)
命题:廖美东 考试时间:2005-4-5
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分.考试时间120分钟.
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型(A或B)用铅笔涂写在答题卡上.
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试题卷上.
3.考试结束,监考人将本试卷和答题卡一并收回.
参考公式:
如果事件A、B互斥,那么 正棱锥、圆锥的侧面积公式
P(A+B)=P(A)+P(B)
![]()
如果事件A、B相互独立,那么 其中c表示底面周长,l表示斜
P(AB)=P(A)P(B) 高或母线长
如果事件A在一次试验中发生的概率是 球的体积公式
P,那么n次独立重复试验中恰好发生k次的概率
![]()
![]() 其中R表示球的半径
其中R表示球的半径
第Ⅰ卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知映射f:A→B,其中集合A={-9,-3,-1,1,3,9},集合B中的元素都是A中的元素在映射f下的象,且对于任意x∈A,在B中和它对应的元素是log3x,则集合B为
A.{1,2,3} B.{0,1,2}
C.{-2,-1,0,1,2} D.{1,2}
2.若α是第三象限角,且cos![]() <0,则
<0,则![]() 是
是
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
3.已知直线a、b,平面α、β,那么下列命题中正确的是
A.若a![]() α,b
α,b![]() β,a⊥b,则α⊥β
β,a⊥b,则α⊥β
B.若a![]() α,b
α,b![]() β,a∥b,则α∥β
β,a∥b,则α∥β
C.若a∥α,a⊥b,则b⊥α
D.若a∥α,a⊥β,则α⊥β
4.设函数f(x)=2-x,函数g(x)的图象与f(x)的图象关于直线y=x对称,函数h(x)的图象由g(x)的图象向右平移1个单位得到,则h(x)为
A.-log2(x-1) B.-log2(x+1)
C.log2(-x-1) D.log2(-x+1)
5.“a>1”是“![]() <1”的
<1”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.若a+b=0,则直线y=ax+b的图象可能是
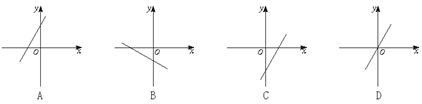
7.设e1、e2是两个不共线向量,若向量a=3e1+5e2与向量b=me1-3e2共线,则m的值等于
A.-![]() B.-
B.-![]() C.-
C.-![]() D.-
D.-![]()
8.Sn为等差数列{an}的前n项之和,若a3=10,a10=-4,则S10-S3等于
A.14 B.6 C.12 D.21
9.设a∈(0,![]() ),则
),则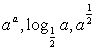 间的大小关系为
间的大小关系为
A.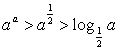 B.
B.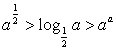
C.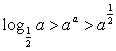 D.
D.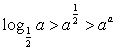
10.椭圆![]() =1(a>b>0)上两点A、B与中心O的连线互相垂直,则
=1(a>b>0)上两点A、B与中心O的连线互相垂直,则![]() 的值为
的值为
A.![]() B.
B.![]()
C.![]() D.
D.![]()
则平均产量较高与产量较稳定的分别是
A.棉农甲,棉农甲 B.棉农甲,棉农乙
C.棉农乙,棉农甲 D.棉农乙,棉农乙
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)
11.已知圆x2+y2-6x-7=0与抛物线y2=2px(p>0)的准线相切,则p=______.
12.x(1-x)4-x3(1+3x)12的展开式中,含x4项的系数为______.
13.若x、y满足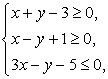 设y=kx,则k的取值范围是______.
设y=kx,则k的取值范围是______.
14.设f(x)是定义在R上的奇函数,且f(x-2)=-f(x),给出下列四个结论:
①f(2)=0;②f(x)是以4为周期的函数;③f(x)的图象关于y轴对称;④f(x+2)=f(-x).
其中所有正确命题的序号是______.
三、解答题(本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤)
15.(本小题满分12分)工人看管三台机床,在某一小时内,三台机床正常工作的概率分别为0.9,0.8,0.85,且各台机床是否正常工作相互之间没有影响,求这个小时内:
(1)三台机床都能正常工作的概率;
(2)三台机床中至少有一台能正常工作的概率.
16.(本小题满分12分)已知A(3,0),B(0,3),C(cosα,sinα).
(1)若![]() =-1,求sin2α的值;
=-1,求sin2α的值;
(2)若![]() ,且α∈(0,π),求
,且α∈(0,π),求![]() 与
与![]() 的夹角.
的夹角.
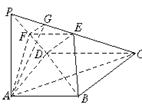
17.(本小题满分13分)如图,已知四边形ABCD为直角梯形,AB∥CD,∠BAD=90°,PA⊥平面ABCD,CD=2,PA=AD=AB=1,E为PC的中点.
(1)求证:EB∥平面PAD;
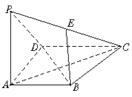 (2)求直线BD与平面PCD所成的角;
(2)求直线BD与平面PCD所成的角;
(3)求二面角A—PC—D的大小.
18.(本小题满分13分)设等比数列{an}中,公比q≠1,Sn=a1+a2+…+an,Tn=![]() .
.
(1)用a1,q,n表示![]() ;
;
(2)若![]() 成等差数列,求q;
成等差数列,求q;
(3)在(2)的条件下,设![]() ,求证:
,求证:![]() .
.
19.(本小题满分14分)已知双曲线![]() =1(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
=1(a>0,b>0)的右准线l2与一条渐近线l交于点P,F是双曲线的右焦点.
(1)求证:PF⊥l;
(2)若PF=3,且双曲线的离心率e=![]() ,求该双曲线方程;
,求该双曲线方程;
(3)延长FP交双曲线左准线l1和左支分别为点M、N,若M为PN的中点,求双曲线的离心率.
20.(本小题满分16分)已知函数f(x)=x3-![]() x2+bx+c.
x2+bx+c.
(1)若f(x)的图象有与x轴平行的切线,求b的取值范围;
(2)若f(x)在x=1时取得极值,且x∈[-1,2]时,f(x)<c2恒成立,求c的取值范围.
2004-2005届高考数学仿真试题(二)(广东)
参考答案
一、1.B 2.B 3.D 4.A 5.A 6.C 7.B 8.A 9.C 10.D
二、11. 2 12. -40 13.[![]() ,2] 14.①②④
,2] 14.①②④
三、15.(1)三台机床都能正常工作的概率为P1=0.9×0.8×0.85=0.612. 6分
(2)三台机床至少有一台能正常工作的概率是
P2=1-(1-0.9)(1-0.8)(1-0.85)=0.997. 12分
16.(1)![]() =(cosα-3,sinα),
=(cosα-3,sinα),![]() =(cosα,sinα-3),
=(cosα,sinα-3),
∴由![]() ·
·![]() =-1,得(cosα-3)cosα+sinα(sinα-3)=-1, 2分
=-1,得(cosα-3)cosα+sinα(sinα-3)=-1, 2分
∴cosα+sinα=![]() , 4分
, 4分
两边平方,得1+sin2α=![]() ,∴sin2α=-
,∴sin2α=-![]() . 6分
. 6分
(2)![]() =(3+cosα,sinα),
=(3+cosα,sinα),
∴(3+cosα)2+sin2α=13, 8分
∴cosα=![]() ,∵α∈(0,π),
,∵α∈(0,π),
∴α=![]() ,sinα=
,sinα=![]() , 9分
, 9分
∴![]() ,
,
设![]() 与
与![]() 的夹角为θ,则
的夹角为θ,则
cosθ=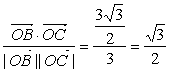 , 11分
, 11分
∴θ=![]() 即为所求. 12分
即为所求. 12分
17.(1)取PD的中点F,连结AF、EF,
则EF![]()
![]() CD,又BA
CD,又BA![]()
![]() CD,
CD,
∴EF![]() BA, 2分
BA, 2分
∴四边形ABEF为平行四边形,∴EB∥FA,
又∵EB![]() 平面PAD,FA
平面PAD,FA![]() 平面PAD,
平面PAD,
∴EB∥平面PAD. 4分
 (2)∵PA⊥平面ABCD,PA
(2)∵PA⊥平面ABCD,PA![]() 平面PAD,
平面PAD,
∴平面PAD⊥平面ABCD,
又∵CD⊥AD,
∴CD⊥平面PAD,又CD![]() 平面PCD,
平面PCD,
∴平面PCD⊥平面PAD,
∵PA=AD,F为PD的中点,
∴AF⊥PD,
∴AF⊥平面PCD,又∵BE∥AF,∴BE⊥平面PCD,
连结DE,则∠BDE为直线BD与平面PCD所成的角, 6分
在Rt△PCD中,![]() ,
,
∴在Rt△ABD中,![]() ,
,
∴在Rt△BDE中,cosBDE=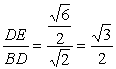 ,
,
∴∠BDE=30°,
即直线BD与平面PCD所成的角为30°. 8分
(3)过F作FG⊥PC于G,连结AG,由三垂线定理得,AG⊥PC,
∴∠FGA为二面角A—PC—D的平面角, 10分
∵Rt△PFG∽Rt△PCD,
∴![]() ,
,
∴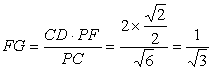 ,
,
在Rt△AFG中,tanFGA=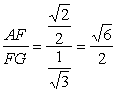 ,
,
∴∠FGA=arctan![]() ,
,
即二面角A—PC—D的大小为arctan![]() . 13分
. 13分
18.(1)Sn=![]() ,而{
,而{![]() }是以
}是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
∴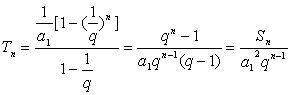 , 2分
, 2分
∴![]() =a12qn-1. 4分
=a12qn-1. 4分
(2)由已知得:-3a12,a12q2,a12q4成等差数列,
∴2a12q2=-3a12+a12q4, 6分
∵a1≠0,∴q4-2q2-3=0,
∵q2>0,∴q2=3,q=±![]() . 8分
. 8分
(3)∵a1=1,q2=3,∴a2n-1=a1q2n-2=(q2)n-1=3n-1,
∴![]() ,
,![]()
两式相减,得
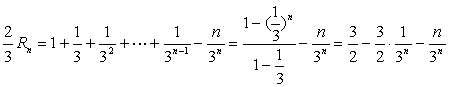 11分
11分
∴![]() . 13分
. 13分
19.(1)右准线为x=![]() ,
,
由对称性不妨设渐近线l为y=![]() x,
x,
则P(![]() ),又F(c,0),
),又F(c,0),
∴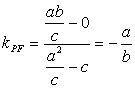 , 2分
, 2分
又∵![]() ,∴kPF·kl=-
,∴kPF·kl=-![]() =-1,
=-1,
∴PF⊥l. 4分
(2)∵PF的长即F(c,0)到l:bx-ay=0的距离,
∴![]() =3,即b=3, 6分
=3,即b=3, 6分
又![]() ,
,
∴![]() ,∴a=4,
,∴a=4,
故双曲线方程为![]() =1. 8分
=1. 8分
(3)PF的方程为:y=-![]() (x-c),
(x-c),
由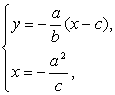 得
得![]() , 10分
, 10分
∵M是PN的中点
∴![]() , 12分
, 12分
∵N在双曲线上,
∴![]() ,
,
即![]() ,
,
令t=e2,则t2-10t+25=0,∴t=5,即e=![]() . 14分
. 14分
20.(1)f′(x)=3x2-x+b,
f(x)的图象上有与x轴平行的切线,则f′(x)=0有实数解, 2分
即方程3x2-x+b=0有实数解,
由Δ=1-12b≥0, 4分
得b≤![]() . 6分
. 6分
(2)由题意,x=1是方程3x2-x+b=0的一个根,设另一根为x0,则
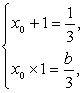 ∴
∴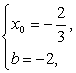 8分
8分
∴f(x)=x3-![]() x2-2x+c,f′(x)=3x2-x-2, 11分
x2-2x+c,f′(x)=3x2-x-2, 11分
当x∈(-1,-![]() )时,f′(x)>0;
)时,f′(x)>0;
当x∈(-![]() ,1)时,f′(x)<0;
,1)时,f′(x)<0;
x∈(1,2)时,f′(x)>0,
∴当x=-![]() 时,f(x)有极大值
时,f(x)有极大值![]() +c,又f(-1)=
+c,又f(-1)=![]() +c,f(2)=2+c,
+c,f(2)=2+c,
即当x∈[-1,2]时,f(x)的最大值为f(2)=2+c,
∵对x∈[-1,2]时,f(x)<c2恒成立,
∴c2>2+c, 12分
解得c<-1或c>2,
故c的取值范围为(-∞,-1)∪(2,+∞). 16分