05 不等式
一、选择题
1．（广东10）设a, b∈R，若a-
＞0，则下列不等式中正确的是（ D ）
A.b-a＞0 B.a3+b3＜0 C.b+a＞0 D.a2-b2＜0
2．（宁夏7）已知a1＞a2＞a3＞0，则使得
都成立的x取值范围是（ B
）
A．
B．
C．
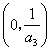D．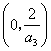
3．(山东7) 不等式
的解集是（ D ）
A．
B．
C．
D．
4．（四川5）不等式
的解集为( A )
（Ａ）
（Ｂ）
（Ｃ）
（Ｄ）
5．(天津8) 已知函数
则不等式
的解集为（ A ）
A．
B．
C．
D．
6．（浙江5）
,且
，则 ( C
)
（A）
（B）
（C）
（D）
7．(重庆7)函数f(x)=
的最大值为 ( B
)
(A)
(B)
(C)
(D)1
二、填空题
1．（北京10）．不等式
的解集是__________．
2．（江苏11）
的最小值为 3
3．（江西13）不等式
的解集为
．
4．（上海1）不等式
的解集是 ．（0，2）
三、解答题
1．（广东17）（本小题满分12分）
某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算，如果将楼房建为x(x≥10)层，则每平方米的平均建筑费用为560+48x（单位：元）.为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用＝平均建筑费用+平均购地费用，平均购地费用＝
）
解：设楼房每平方米的平均综合费为f（x）元，则
令 
得
当 
时，
；当 
时，
因此 当时，f（x）取最小值
；
答：为了楼房每平方米的平均综合费最少，该楼房应建为15层．
2．（江苏选修）设a，b，c为正实数，求证：
．
证明：因为
为正实数，由平均不等式可得
即
所以
，
而
所以
3．(湖北19).（本不题满分12分）
如图，要设计一张矩形广告，该广告含有大小相等的左右两个矩形栏目（即图中阴影部分），这两栏的面积之和为18000cm2,四周空白的宽度为10cm，两栏之间的中缝空白的宽度为5cm，怎样确定广告的高与宽的尺寸（单位：cm），能使矩形广告面积最小？
解法1：设矩形栏目的高为a cm，宽为b cm，则ab=9000. ①
广告的高为a+20，宽为2b+25，其中a＞0，b＞0.
广告的面积S＝(a+20)(2b+25)
＝2ab+40b+25a+500＝18500+25a+40b
≥18500+2
=18500+
当且仅当25a＝40b时等号成立，此时b=
,代入①式得a=120，从而b=75.
即当a=120，b=75时,S取得最小值24500.
故广告的高为140 cm,宽为175 cm时，可使广告的面积最小.
解法2：设广告的高为宽分别为x cm，y cm，则每栏的高和宽分别为x－20，
其中x＞20，y＞25
两栏面积之和为2(x－20)
,由此得y=
广告的面积S=xy=x(
)＝x,
整理得S=
因为x－20＞0，所以S≥2
当且仅当
时等号成立，
此时有(x－20)2＝14400(x＞20)，解得x=140，代入y=
+25,得y＝175，
即当x=140，y＝175时，S取得最小值24500，
故当广告的高为140 cm，宽为175 cm时，可使广告的面积最小.