高考理科数学极限与导数复习(理)
1 考点回顾
1.数学归纳法是证明关于自然数![]() (改为“与自然数n有关” )的命题的一种方法,在高中数学中有着非常重要的用途,是高考命题的热点内容之一。
(改为“与自然数n有关” )的命题的一种方法,在高中数学中有着非常重要的用途,是高考命题的热点内容之一。
2.函数极限和数列极限仍然以选择题或填空题为主,主要考查基本计算,有时也在解答题的最后一问出现,中等或偏易的难度(文科不要求函数的极限)。
3.导数的概念及其运算是导数应用的基础,是高考重点考查的内容。考查方式以客观题为主,主要考查导数的基本公式和运算法则,以及导数的几何意义。
4.导数的应用是高中数学中的重点内容,导数已由解决问题的工具上升到解决问题必不可少的工具,特别是利用导数来解决函数的单调性与最值问题、证明不等式问题等,是(改为“已成为”)高考热点问题。选择填空题侧重于利用导数确定函数的单调性、单调区间和最值问题,解答题侧重于导数的综合应用,即与函数、不等式、数列的综合应用。
5.应用导数解决实际问题,关键是建立恰当的数学模型(函数关系),如果函数在给定区间内只有一个极值点,此时函数在这点有极大(小)值,而此时不用和端点值进行比较,也可以得知这就是最大(小)值。
2 经典例题剖析
考点一:数学归纳法
例1:设正数数列![]() 的前
的前![]() 项和
项和![]() 满足
满足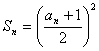 。求
。求![]() ,猜想
,猜想![]() 的通项公式,并用数学归纳法证明;设
的通项公式,并用数学归纳法证明;设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() 。
。
解析:(1)由题设可求![]() ,猜想数列
,猜想数列![]() 的通项公式为:
的通项公式为: ![]() ,下面用数学归纳法证明:
,下面用数学归纳法证明:
①当![]() 时,显然成立;
时,显然成立;
②假设当![]() 时,猜想成立,即
时,猜想成立,即![]() ,那么当
,那么当![]() 时,
时,
由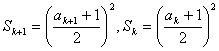
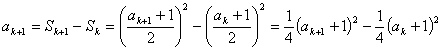
化简可得:![]() ,即
,即![]() ,
,![]() 或
或![]() ,又
,又![]() ,
, ![]() ,即
,即![]() ,所以,当
,所以,当![]() 时,猜想成立。
时,猜想成立。
由①、②可知,对一切![]() ,有
,有![]() 。
。
(2)由![]() ,
, ![]() ,则
,则![]()
![]() 所以
所以![]() 。
。
答案:(1)证明见解析;(2)![]()
点评:归纳、猜想、证明这一解题模式,是解决数列问题的常用方法,在证明过程中,要注意由n=k到n=k+1时,归纳假设的合理运用;另外,注意裂项项消法求和及常用的数列极限。
考点二:数列的极限
例4:已知数列![]() 满足
满足![]() ,求
,求![]() 。
。
解析:由![]() ,得
,得![]() ,∴数列
,∴数列![]() 为常数列.
为常数列.
∵![]() , ∴
, ∴![]() ,∴
,∴![]() ,∴数列
,∴数列![]() 是公比为
是公比为![]() ,首项为
,首项为![]() 的等比数列.,∴
的等比数列.,∴![]() ,∴
,∴![]() ,∴
,∴![]() 。
。
答案:![]()
点评:本题主要考查特殊数列通项公式的求解和数列的极限。难点在于求出数列![]() 的通项公式。
的通项公式。
考点三:函数的极限和连续性
例5:设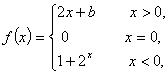 试确定
试确定![]() 的值,使
的值,使![]() 存在。
存在。
解析:![]() ,
,![]() ,
,
当且仅当![]() 时,有
时,有![]()
所以,当![]() 时,原函数极限存在。
时,原函数极限存在。
答案:![]()
点评:函数在某点处存在极限与函数在该点处连续的概念不同。存在极限只要求在该点处的左右极限相等;而在该点连续则还要求左右极限的值同时等于函数在该点处的函数值。
例6:设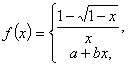
![]() ,(1)求
,(1)求![]() ;(2)求
;(2)求![]() 的值使
的值使![]() 在
在![]() 处连续。
处连续。
解析:(1)当![]() 时,
时,![]()
![]() ;当
;当![]() 时,
时,![]() ,
,![]() 。所以,
。所以,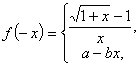
![]() 。
。
(2)![]() ,
,![]() 。因为
。因为![]() 在
在![]() 处连续,则
处连续,则![]() ,此时
,此时![]() 。
。
答案: (1)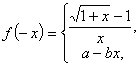
![]() ;(2)
;(2)![]()
点评:本题主要考查函数连续的概念,应和上一题进行对比。
考点四: 导数的概念及其运算
例3:用定义求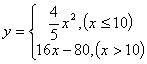 在点
在点![]() 处的导数。
处的导数。
解析:分别求出![]() 在
在![]() 处的左右极限,
处的左右极限,

![]()
![]() ,即
,即![]() 。
。
答案:![]()
点评:导数的定义给出了求导的最基本的方法,如果用求导公式、法则都无法求导时,就要考虑用定义法去求导,本题是分段函数在分界点处的导数,只能用定义法去求,这时要注意,只有当左、右导数都存在且相等时,函数在这点的导数才是存在的。
考点五:函数的最值与极值
例2:求函数![]() 在
在![]() 上的最大值和最小值。
上的最大值和最小值。
解析:在闭区间上连续函数有最大值和最小值,于是,应用导数得![]()
令 ![]() 化简为
化简为 ![]() 解得
解得![]() (舍),
(舍),![]() 。当
。当![]() 单调递增;当
单调递增;当![]() 单调递减。所以
单调递减。所以![]() 为函数
为函数![]() 的极大值。
的极大值。
又因为![]() 所以 函数
所以 函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,函数
,函数![]() 在
在![]() 上的最大值为
上的最大值为![]() 。
。
答案:最小值为![]() ,最大值为
,最大值为![]() 。
。
点评:本小题主要考查函数的导数计算,利用导数讨论函数的性质,判断函数的最大值、最小值以及综合运算能力。
考点六:导数的应用
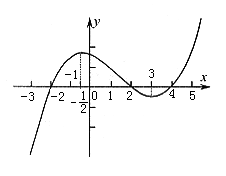
例7:如果函数![]() 的导函数的图象如图所示,给出下列判断:
的导函数的图象如图所示,给出下列判断:
①函数![]() 在区间
在区间![]() 内单调递增;
内单调递增;
②函数![]() 在区间
在区间![]() 内单调递减;
内单调递减;
③函数![]() 在区间
在区间![]() 内单调递增;
内单调递增;
④当![]() 时,函数
时,函数![]() 有极小值;
有极小值;
⑤当![]() 时,函数
时,函数![]() 有极大值;
有极大值;
则上述判断中正确的是________________。
解析:由导函数图像可知,当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上为减函数,同理可知:
上为减函数,同理可知:![]() 在
在![]() 上为减函数。
上为减函数。![]() 在
在![]() 和
和![]() 上为增函数。所以可以排除①和②,③是正确的。又由于函数
上为增函数。所以可以排除①和②,③是正确的。又由于函数![]() 在
在![]() 的左侧递增,右侧递减,所以
的左侧递增,右侧递减,所以![]() 时,函数有极大值;在
时,函数有极大值;在![]() 左右两侧函数的导数均为正数,所以
左右两侧函数的导数均为正数,所以![]() 不是函数的极值点,从而排除④和⑤。
不是函数的极值点,从而排除④和⑤。
答案: ③
点评:本题主要考查函数的单调性和极值与导数的关系,属于逆向思维的题目。
例8:已知向量![]() 在区间
在区间![]() 上是增函数,求
上是增函数,求![]() 的取值范围。
的取值范围。
解析:解法1:依定义![]()
![]() ,
,![]()

开口向上的抛物线,故要使![]() 在区间(-1,1)上恒成立
在区间(-1,1)上恒成立![]()
![]()
![]()
![]() .
.
解法2:依定义![]()
![]() ,
,![]()
![]() 的图象是开口向下的抛物线,
的图象是开口向下的抛物线, ![]() ,
,
![]() ,
,![]() 。
。
答案:![]()
点评:本小题主要考查平面向量数量积的计算方法、利用导数研究函数的单调性,以及运用基本函数的性质分析和解决问题的能力。
例9:(07年海南理科)设函数![]() ,(1)若当
,(1)若当![]() 时,
时,![]() 取得极值,求
取得极值,求![]() 的值,并讨论
的值,并讨论![]() 的单调性;(2)若
的单调性;(2)若![]() 存在极值,求
存在极值,求![]() 的取值范围,并证明所有极值之和大于
的取值范围,并证明所有极值之和大于![]() .
.
解析:(1)![]() ,依题意有
,依题意有![]() ,故
,故![]() .
.
从而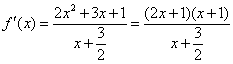 .
.
![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
从而,![]() 分别在区间
分别在区间![]() 单调增加,在区间
单调增加,在区间![]() 单调减少.
单调减少.
(2)![]() 的定义域为
的定义域为![]() ,
,![]() .
.
方程![]() 的判别式
的判别式![]() .
.
①若![]() ,即
,即![]() ,在
,在![]() 的定义域内
的定义域内![]() ,故
,故![]() 的极值.
的极值.
②若![]() ,则
,则![]() 或
或![]() .若
.若![]() ,
,![]() ,
,![]() .
.
当![]() 时,
时,![]() ,当
,当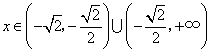 时,
时,![]() ,所以
,所以![]() 无极值.若
无极值.若![]() ,
,![]() ,
,![]() ,
,![]() 也无极值.
也无极值.
③若![]() ,即
,即![]() 或
或![]() ,则
,则![]() 有两个不同的实根
有两个不同的实根![]() ,
,![]() .
.
当![]() 时,
时,![]() ,从而
,从而![]() 有
有![]() 的定义域内没有零点,故
的定义域内没有零点,故![]() 无极值.
无极值.
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知![]() 在
在![]() 取得极值.
取得极值.
综上,![]() 存在极值时,
存在极值时,![]() 的取值范围为
的取值范围为![]() .
.![]() 的极值之和为
的极值之和为
![]() .
.
答案: (1)![]() ;(2)见详解。
;(2)见详解。
点评:本题主要考查对极值概念的理解以及对函数导数的综合运用。
3 方法总结与2008年高考预测
(分析2008年高考命题趋势,对命题难度,内容,热点等作总结)
(一)方法总结
1.极限的概念和运算法则是微积分中最重要的工具,也是学好导数的基础。它是历年高考的重点考查内容,多与分类讨论相结合。通常与数列结合的题目要多一些,解答时要求先求出数列的通项公式或是前![]() 项和公式再求极限。求函数的极限时,经常要用到常见函数的极限及两个重要极限(解决函数极限的小题时可用洛毕达法则)。通过恒等变形用函数极限的四则运算法则求相关函数的极限,或利用初等函数在其定义域内每一点处的极限值等于该点函数值求函数的极限或利用函数的极限判定函数在给定点处的连续性。归纳法也是本章常见的考查点,一定要注意用数学归纳法解题时的步骤。
项和公式再求极限。求函数的极限时,经常要用到常见函数的极限及两个重要极限(解决函数极限的小题时可用洛毕达法则)。通过恒等变形用函数极限的四则运算法则求相关函数的极限,或利用初等函数在其定义域内每一点处的极限值等于该点函数值求函数的极限或利用函数的极限判定函数在给定点处的连续性。归纳法也是本章常见的考查点,一定要注意用数学归纳法解题时的步骤。
2.导数是中学限选内容中较为重要的知识,由于其应用的广泛性,为我们解决所学过的有关函数问题提供了一般性方法,是解决实际问题强有力的工具。导数的概念及其运算是导数应用的基础,是高考重点考查的对象。要牢记导数公式,熟练应用导数公式求函数的导数,掌握求导数的方法。应用导数解决实际问题的关键是要建立恰当的数学模型,了解导数概念的实际背景。
(二)2008年高考预测
函数极限和数列极限仍然以选择或填空题为主,有时会在解答题的最后一问出现难度中等或偏易。(文科生对函数极限不做要求)
导数的考查方式以客观题为主,主要考查求导数的基本公式和法则,以及导数的几何意义。也可以解答题的形式出现,即以导数的几何意义为背景设置成导数与解析几何的综合题。导数的应用是重点,侧重于利用导数确定函数的单调性和极值、最值、值域问题,侧重于导数的综合应用,即导数与函数、数列、不等式的综合应用。
4 强化训练
(要求选择填空解答兼有并留有解答空间,便于用户直接应用)
1 选择题
1.已知曲线![]() 的一条切线的斜率为
的一条切线的斜率为![]() ,则切点的横坐标为( )
,则切点的横坐标为( )
A.1 B.2 C.3 D.4
2.已知对任意实数![]() ,有
,有![]() ,且
,且![]() 时,
时,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.下列函数在x =0处连续的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.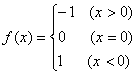
4.已知函数![]() 既存在极大值又存在最小值,则实数m的取值范围是( ).
既存在极大值又存在最小值,则实数m的取值范围是( ).
A![]()
![]() B.
B.![]()
C.![]() D.
D. ![]()
5.函数![]() 在
在![]() 上的最小值是 ( )
上的最小值是 ( )
A. ![]() B. 1 C.
B. 1 C. ![]() D. 5
D. 5
6.![]() 的值为( ).
的值为( ).
A.![]() B.0
C.
B.0
C.![]() D.1
D.1
7. 设![]() 在
在![]() 内单调递增,
内单调递增,![]() ,则
,则![]() 是
是![]() 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
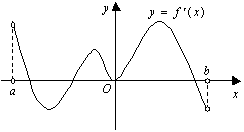
8.函数![]() 的定义域为开区间
的定义域为开区间![]() ,导函数
,导函数![]() 在
在![]() 内的图象如图所示,则函数
内的图象如图所示,则函数![]() 在开区间
在开区间![]() 内有极小值点( )
内有极小值点( )
A.1个
B.2个
C.3个
D. 4个
9.已知![]() ,下面结论正确的是( )
,下面结论正确的是( )
A.![]() 在
在![]() 处连续 B.
处连续 B.![]() C.
C.![]() D.
D.![]()
10.函数![]() 在下面哪个区间内是增函数 ( )
在下面哪个区间内是增函数 ( )
A.(![]() ,
,![]() ) B.(
) B.(![]() ,2
,2![]() ) C.(
) C.(![]() ,
,![]() ) D.(2
) D.(2![]() ,3
,3![]() )
)
11.函数![]() 在点
在点![]() 和
和![]() 处的极限值都是0,而在点
处的极限值都是0,而在点![]() 处不连续,则不等式
处不连续,则不等式![]() 的解集为( )
的解集为( )
A.(-2,1) B.(-∞,-2)∪(2,+∞)
C.(-2,1)∪(2,+∞) D.(-∞,-2)∪(1 , 2)
12.若数列![]() 的通项公式是
的通项公式是![]() ,
,![]() ,则
,则
![]() 等于 ( )
等于 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2 填空题
13. 若![]() ,则
,则![]() ___1___,
___1___,![]() __1____。
__1____。
14. 已知函数![]() 的图象在点
的图象在点![]() 处的切线方程是
处的切线方程是![]() ,则
,则![]() .
.
15. 已知点![]() ,其中N为正整数,设Sn表示△ABC外接圆的面积,则
,其中N为正整数,设Sn表示△ABC外接圆的面积,则![]() =
。
=
。
16. 已知函数y=f(x)在R上处处可导,f(0)=0,当![]() 0时,xf’(x)>0。给出下列四个判断:
0时,xf’(x)>0。给出下列四个判断:
① f(–2)< f(–1); ② y= f(x)不可能是奇函数;
③存在区间[–a,a],使得当![]() 、
、![]() 成立;
成立;
④ y = x f(x)在R上单调递增。
判断正确的序号是___________________。(请填上所有判断正确的序号)
3 解答题
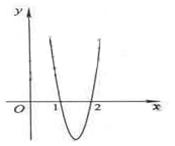
17. 已知函数![]() 在点
在点![]() 处取得极大值
处取得极大值![]() ,其导函数
,其导函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,如图所示.求:
,如图所示.求:
(Ⅰ)![]() 的值;
的值;
(Ⅱ)![]() 的值.
的值.
18. 已知函数![]() 处取得极值2。
处取得极值2。
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)当m满足什么条件时,![]() 在区间
在区间![]() 为增函数;
为增函数;
(Ⅲ)若![]() 图象上任意一点,直线
图象上任意一点,直线![]() 的图象切于P点,求直线L的斜率的取值范围。
的图象切于P点,求直线L的斜率的取值范围。
19. 已知函数![]()
(Ⅰ)若![]() 单调递减,求a的取值范围。
单调递减,求a的取值范围。
(Ⅱ)当a=4时,设![]() ,是否存在实数m,使得y=
,是否存在实数m,使得y=![]() 的图象
的图象![]() 的图象有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由。
的图象有且只有三个不同的交点?若存在,求出m的取值范围;若不存在,说明理由。
20. 已知函数![]() 。
。
(Ⅰ)设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅱ)若对任意![]() 恒有
恒有![]() ,求
,求![]() 的取值范围。
的取值范围。
21. 设![]() 是
是![]() 的两个极值点,
的两个极值点,![]() 的导函数是
的导函数是![]()
(Ⅰ)如果![]() ,求证:
,求证:![]() ;
;
(Ⅱ)如果![]() ,求
,求![]() 的取值范围 ;
的取值范围 ;
(Ⅲ)如果![]() ,且
,且![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最大值。
的最大值。
22. 已知函数![]()
![]()
(Ⅰ)判断![]() 的奇偶性;
的奇偶性;
(Ⅱ)在![]() 上求函数
上求函数![]() 的极值;
的极值;
(Ⅲ)用数学归纳法证明:当![]() 时,对任意正整数
时,对任意正整数![]() 都有
都有![]()
解析答案:
(一)选择题:
1. A 2. B 3.A 4.B 5.B 6.A 7.B 8.A 9.D 10.B 11.C 12.C
(二)填空题:
13. ![]() 1,
1,![]() 1 14. 3 15.
1 14. 3 15. ![]() 16. ②③④
16. ②③④
(三)解答题:
17. 解法一:
(Ⅰ)由图像可知,在![]() 上
上![]()
![]() ,
,
在![]() 上
上![]() ,在
,在![]() 上
上![]()
故![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
因此![]() 在
在![]() 处取得极大值,所以
处取得极大值,所以![]()
(Ⅱ)![]()
由![]()
得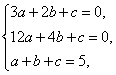 解得
解得![]()
解法二:
(Ⅰ)同解法一
(Ⅱ)设![]()
又![]()
所以![]()
![]()
由![]()
即![]()
得![]()
所以![]()
18. (Ⅰ)![]()
由已知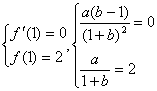
![]()
![]()
(Ⅱ)![]()
![]()
又![]() 在
在![]()
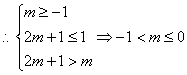 )
)
(Ⅲ)直线I在P点的切线斜率![]()
令![]()
当![]()
![]() )
)
19. (Ⅰ)![]() ………………1分)
………………1分)
当![]() 时,
时,![]() ,在
,在![]()
![]() 上单调递减,符合题意
上单调递减,符合题意
当![]() 时,
时,![]() ,
,![]() 恒成立。
恒成立。![]() 上单调递减,符合题意
上单调递减,符合题意
当![]() 时,
时,![]() ,在
,在 ![]() 上单调递减
上单调递减
则若![]() 上单调递减,需
上单调递减,需![]()
综合以上可知,若![]() 在
在![]() 单调减减,a的取值范围是
单调减减,a的取值范围是![]()
(Ⅱ)函数![]() 的图象与
的图象与![]() 的图象有且只有三个不同的交点,即函数
的图象有且只有三个不同的交点,即函数
![]() 的图象与x轴的正半轴有且只有三个不同的交点。
的图象与x轴的正半轴有且只有三个不同的交点。
∴![]()
∵![]() ,
,
当![]() 是增函数;
是增函数;
当![]() 是减函数;
是减函数;
当![]() 是增函数;
是增函数;
当![]() ,或
,或![]() 时,
时,![]() =0
=0
∴![]()
∵当![]() 充分接近0时,
充分接近0时,![]() ,当
,当![]() 充分大时,
充分大时,![]()
∴要使![]() 的图象与
的图象与![]() 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须
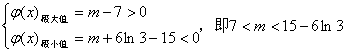
所在存在实数![]() ,使得函数
,使得函数![]() 的图象有且只有三个不同的交点,
的图象有且只有三个不同的交点,![]() 的取值范围为
的取值范围为![]() 。
。
20. (I) ![]() 的定义域为
的定义域为![]()
![]()
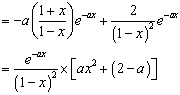
因为![]() (其中
(其中![]() )恒成立,所以
)恒成立,所以![]()
⑴ 当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上为增函数;
上为增函数;
⑵ 当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上为增函数;
上为增函数;
⑶ 当![]() 时,
时,![]() 的解为:
的解为:![]()
(其中![]() )
)
所以f(x)在各区间内的增减性如下表:
| 区间 |
|
|
|
|
|
| + |
| + | + |
|
| 增函数 | 减函数 | 增函数 | 增函数 |
(II)显然![]()
⑴ 当![]() 时,
时,![]() 在区间
在区间![]() 上是增函数,
上是增函数,
所以对任意![]() 都有
都有![]() ;
;
⑵ 当![]() 时,
时,![]() 是
是![]() 在区间
在区间![]() 上的最小值,即
上的最小值,即![]() ,
,
这与题目要求矛盾;
⑶ 若![]() ,
,![]() 在区间
在区间![]() 上是增函数,所以对任意
上是增函数,所以对任意![]() 都有
都有![]() 。
。
综合⑴、⑵、⑶ ,a的取值范围为![]()
21. (I)证明:![]()
![]() 是方程
是方程![]() 的两个根
1分
的两个根
1分
由![]() 且
且![]() 得
得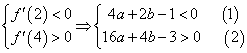 2分
2分
![]() 得
得![]()
![]() 3分
3分
(Ⅱ)解:由第(1)问知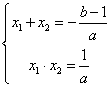 由
由![]() ,两式相除得
,两式相除得
![]() 即
即![]() 4分
4分
①当![]() 时,由
时,由![]()
![]() 即
即![]()
![]() ,
, ![]() 5分
5分
令函数![]() ,则
,则![]()
![]() 在
在![]() 上是增函数
上是增函数
![]() 当
当![]() 时,
时,![]() ,即
,即![]() 7分
7分
②当![]() 时,
时,![]()
![]() 即
即![]()
![]()
令函数![]() 则同理可证
则同理可证![]() 在
在![]() 上是增函数
上是增函数
![]() 当
当![]() 时,
时,![]()
综①②所述,![]() 的取值范围是
的取值范围是![]()
(Ⅲ)解:![]() 的两个根是
的两个根是![]() ,
,![]() 可设
可设![]()
![]() 10分
10分
![]() 又
又![]()
![]()
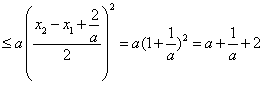
g(x) ![]()
当且仅当![]() ,即
,即![]() 时取等号
时取等号
![]() 当
当![]() 时,
时,![]()
![]() 在
在![]() 上是减函数
上是减函数
![]()
22. (Ⅰ) 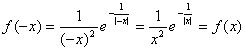
![]() 。
。
(Ⅱ)当![]() 时,
时,![]()
![]()
令![]() 有
有![]() ,
,
当x变化时![]() 的变化情况如下表: 由表可知:
的变化情况如下表: 由表可知:
|
|
|
| ( |
|
| + | 0 | - |
|
| 增 | 极大值 | 减 |
当![]() 时
时![]() 取极大值
取极大值![]() .
.
(Ⅲ)当![]() 时
时![]()
考虑到:![]() 时,不等式
时,不等式![]() 等价于
等价于![]() …(1)
…(1)
所以只要用数学归纳法证明不等式(1)对一切![]() 都成立即可
都成立即可
(i)当![]() 时,设
时,设![]()
![]() ,
,
故![]() ,即
,即![]()
所以,当![]() 时,不等式(1)都成立
时,不等式(1)都成立
(ii)假设![]() 时,不等式(1)都成立,即
时,不等式(1)都成立,即![]()
当![]() 时设
时设![]()
有![]()
故![]() 为增函数,
为增函数,
所以,![]() ,即
,即![]() ,
,
这说明当![]() 时不等式(1)也都成立,
时不等式(1)也都成立,
根据(i)(ii)可知不等式(1)对一切![]() 都成立,
都成立,
故原不等式对一切![]() 都成立.
都成立.
6 复习建议
1.极限内容和简单的函数求导在高考中以填空题和解答题为主。考生应立足基础只是和基本方法的复习,以课本题目为主,以熟练技能,巩固概念为目标。
2.对极限和导数的概念以及导数的实际背景一定要深入了解。
3.题目的难度要控制好,不要太难,应以方法的本质为主。
4.有意识地与解析几何(特别是切线、最值)、函数的单调性、函数的极值、最值、二次函数、方程、不等式等进行交汇,综合运用。特别是精选一些以导数为工具分析和解决一些函数问题,以及一些实际问题中的最大(小)值问题。