08高考理科数学湛江市第四次月考试题
时间:120分钟 分数:150分
一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只
有一项符合要求的
1.已知全集U=R,集合![]()
A.{xx<2} B.{xx≤2} C.{x-1<x≤2} D.{x-1≤x<2}
 2.
2.![]() 辆汽车通过某一段公路时的时速的频率分布直方图
辆汽车通过某一段公路时的时速的频率分布直方图
如右图所示,时速在![]() 的汽车大约有
的汽车大约有
![]() .
.![]() 辆
辆 ![]() .
. ![]() 辆
辆 ![]() .
.![]() 辆
辆 ![]() .80辆
.80辆
3.有关命题的说法错误的是 ( )
A.若![]() 为假命题,则
为假命题,则![]() 、
、![]() 均为假命题.
均为假命题.
B.
“![]() ”是“
”是“![]() ”的充分不必要条件.
”的充分不必要条件.
C.命题“若![]() 则
则 ![]() ”的逆否命题为:“若
”的逆否命题为:“若![]() , 则
, 则![]() ”.
”.
D.对于命题![]() :
:![]() 使得
使得![]() . 则
. 则![]()
![]() :
:![]() 均有
均有![]() .
.
4.下列关系中,成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.{an}为等差数列,Sn为其前n项和,S5<S6,S6=S7>S8,则下列错误的是( )
A. d>0 B. a7=0 C. S9<S5 D. S6与S7均为Sn的最大值
6.在![]() ABC中,
ABC中,![]() ,
,![]() ,面积为
,面积为![]() ,那么
,那么![]() 的长度为( )
的长度为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)
![]()
7.已知![]() ,A是由直线
,A是由直线![]() 围成的曲边三
围成的曲边三
角形的平面区域,若向区域![]() 上随机投一点P,则P落在区域A内的概率为
上随机投一点P,则P落在区域A内的概率为
A
![]() B
B![]() C
C ![]() D
D ![]()
8.已知![]() 是以
是以![]() 为周期的偶函数,当
为周期的偶函数,当![]() 时,
时,![]() ,那么在区间
,那么在区间![]() 内,关于
内,关于![]() 的方程
的方程![]() (
(![]() 且
且![]() )有
)有![]() 个不同的根,则
个不同的根,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共6小题,每小题5分,满分30分
9.设二项式![]() 展开式各项的系数和为P,二项式系数之和为S,P+S=72,则正整数
展开式各项的系数和为P,二项式系数之和为S,P+S=72,则正整数![]() ,展开式中常数项的值为
。
,展开式中常数项的值为
。
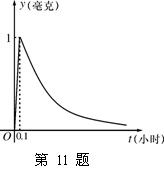 10.如图,函数
10.如图,函数![]() 的图象在点P处的切线方程是
的图象在点P处的切线方程是 ![]() ,则
,则![]() =
.
=
.
 |
.
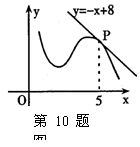
11.为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为![]() (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(a为常数),如图所示,根据图中提供的信息,回答下列问题:
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为 .
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 小时后,学生才能回到教室.
12.已知向量a、b满足:a=3,b=4,a、b的夹角是120°,则a+2b=___________.
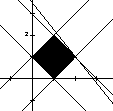
13.平面内满足不等式组1≤x+y≤3,—1≤x—y≤1,x≥0,y≥0的所有点中,使目标函数z=5x+4y取得最大值的点的坐标是 _____ .
14.下面有五个命题:
①函数y=sin4x−−cos4x的最小正周期是![]() .
②终边在y轴上的角的集合是{aa=
.
②终边在y轴上的角的集合是{aa=![]() .
.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数![]()
⑤函数![]() 其中真命题的序号 (写出所有真命题的编号)。
其中真命题的序号 (写出所有真命题的编号)。
三、解答题:本大题共有6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
15.设正项等比数列![]() 的前
的前![]() 项和为
项和为![]() , 已知
, 已知![]() ,
,![]() .
.
(Ⅰ)求首项![]() 和公比
和公比![]() 的值;
的值;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
16.已知向量![]() ,
,![]() 与
与![]() 为共线向量且
为共线向量且![]()
Ⅰ)求![]() 的值; Ⅱ)求
的值; Ⅱ)求![]() 的值
的值
17.一个口袋中装有大小相同的2个白球和4个黑球.
(Ⅰ)采取放回抽样方式,从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)采取不放回抽样方式,从中摸出两个球,求摸得白球的个数的期望和方差.
18.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(Ⅰ)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(Ⅱ)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=![]() 的表达式;
的表达式;
(Ⅲ)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
19.已知定义域为R的函数![]() 是奇函数,
是奇函数,
Ⅰ)求![]() 的值
的值
Ⅱ)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
20.(14分)已知点P在曲线![]() 上,曲线C在点P处的切线与函数
上,曲线C在点P处的切线与函数![]() 的图象交于点A,与
的图象交于点A,与![]() 轴交于点B,设点P的横坐标为
轴交于点B,设点P的横坐标为![]() ,点A,B的横坐标分别为
,点A,B的横坐标分别为 ![]() ,记
,记![]()
Ⅰ)求![]() 的解析式
的解析式
Ⅱ)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式
的通项公式
Ⅲ)在Ⅱ)的条件下,当![]() 时,证明不等式
时,证明不等式![]()
答题卡
|
| 一 | 二 | 三 | 总 分 | |||||
| 15 | 16 | 17 | 18 | 19 | 20 | ||||
| 得分 | |||||||||
一、选择题:(共8小题,每小题5分,共计40分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 选 项 |
|
|
|
|
|
|
|
|
二、填空题:(共6小题,每小题5分,共计30分)
9. 10.
11. 12.
13. 14.
三、解答题:(共6小题,共计80分,解答写出文字说明、证明过程或演算步骤)
15.(本小题满分12分)

16.(本小题满分12分)
| |
17.(本小题满分14分)
| |
18.(本小题满分14分)
| |
19.(本小题满分14分)
| |
20.(本小题满分14分)
| |
参考答案
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 选 项 | B | C | A | A | A | D | D | D |
9、3,9 10、2 11、![]()
![]() ,0.6 12、7 13、(2,1) 14、(1)(4)
,0.6 12、7 13、(2,1) 14、(1)(4)
1、![]() ,所以
,所以![]()
![]() ,选B
,选B
2、![]() 的频率/组距=0.03,频率=0.03×10=0.3,频数=0.3×200=60,选C
的频率/组距=0.03,频率=0.03×10=0.3,频数=0.3×200=60,选C
3、选A,![]() 为假命题,p和q可能是一真一假
为假命题,p和q可能是一真一假
4、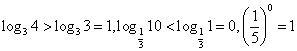 ,选A
,选A
5、由S5<S6得![]() ,由S6=S7得
,由S6=S7得![]() ,
,![]() ,选A
,选A
6、由![]() 得
得
![]()
![]() ,选D
,选D
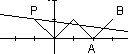 8、根据题意画出
8、根据题意画出![]() 在区间
在区间![]() 上的图象,令
上的图象,令![]() 则为经过点(-1,1)斜率为k的直线,如图所示,要使方程有4个不同的根,两图象必有4个交点,则直线必然在点A、B之间,由
则为经过点(-1,1)斜率为k的直线,如图所示,要使方程有4个不同的根,两图象必有4个交点,则直线必然在点A、B之间,由![]() 可知,选D
可知,选D
9、令x=1可得![]() ,而
,而![]() ,因而
,因而
![]() ,
,![]() ,常数项
,常数项![]()
 10、由图可知P的横坐标为5,
10、由图可知P的横坐标为5,![]() 即P(5,3),
即P(5,3),![]()
![]() ,
,
12、![]()
13、如图,填(2,1)
14、(1)![]()
![]() ,正确
,正确
(2)集合表示的是所有坐标轴上的角,错误
(3)只有一个,错误
(4)正确
(5)![]() 在
在![]() 上是增函数,错误
上是增函数,错误
填(1)(4)
15、解:由![]() 得
得![]() ................................................................ 2分
................................................................ 2分
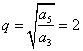 ........................................................................................................ 4分
........................................................................................................ 4分
![]() ..................................................................................................... 6分
..................................................................................................... 6分
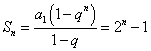 ,
,![]() ...................................................................... 12分
...................................................................... 12分
16、解:![]() 与
与![]() 为共线向量
为共线向量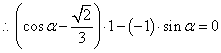 ........................ 3分
........................ 3分
![]() ........................................................................................... 6分
........................................................................................... 6分
平方得:![]() ............................................................................... 7分
............................................................................... 7分
![]() .............................................................................. 8分
.............................................................................. 8分
![]()
![]()
![]() .............................................................................................. 10分
.............................................................................................. 10分
![]() ............................................................................................ 12分
............................................................................................ 12分
17、解法一 “有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,记“有放回摸球两次,两球恰好颜色不同”为事件A,
∵“两球恰好颜色不同”共2×4+4×2=16种可能,![]() ............... 6分
............... 6分
解法二 “有放回摸取”可看作独立重复实验
∵每次摸出一球得白球的概率为![]()
∴“有放回摸两次,颜色不同”的概率为![]() ........................... 6分
........................... 6分
(2)设摸得白球的个数为![]() ,依题意得
,依题意得
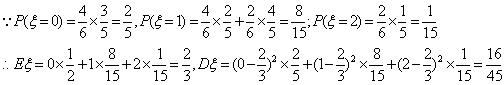
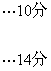
18、解:(1)多订购的零件x-100个,每个零件降低价格:0.02×(x-100),
列方程得:![]() ...................................................................... 4分
...................................................................... 4分
解得:![]()
答:当一次订购量为550个时,零件的实际出厂价恰降为51元。
(2)由(1)得当![]() 时
时![]()
当![]() 时P=51
时P=51
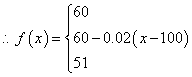
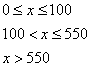 ..................................................... 9分
..................................................... 9分
(3)当x=500时![]() .............................................. 10分
.............................................. 10分
总利润![]() ........................................................................... 12分
........................................................................... 12分
当x=1000时P=51
总利润![]() ........................................................................ 14分
........................................................................ 14分
19、解:![]() 为奇函数
为奇函数![]()
![]() ........................................ 3分
........................................ 3分
由![]() 得:
得: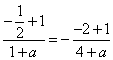 ,解得:
,解得:![]() ...................................... 6分
...................................... 6分
(2)由(1)得![]() 为R上的减函数............................ 8分
为R上的减函数............................ 8分
![]() 为奇函数
为奇函数 ![]() .................................................... 9分
.................................................... 9分
由![]() 得:
得:![]()
![]() .................................................................................................... 12分
.................................................................................................... 12分
要使上式恒成立,需:![]() 解得:
解得:![]() ................................ 14分
................................ 14分
20、(1)解:![]() .................................................................................. 1分
.................................................................................. 1分
切线方程为![]() ........................................................ 2分
........................................................ 2分
与![]() 联立得:
联立得:![]() ............................................................................. 3分
............................................................................. 3分
令y=0得:![]() .............................................................................................. 4分
.............................................................................................. 4分
![]() (
(![]() )........................................................................... 5分
)........................................................................... 5分
(2)由![]() 得:
得:![]() ............................................................. 6分
............................................................. 6分
两边取倒数得:![]()
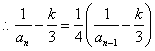 .............................. 7分
.............................. 7分
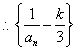 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列(
为公比的等比数列(![]() 时)
时)
或是各项为0的常数列(k=3时),此时![]() ..................................................... 9分
..................................................... 9分
![]() 时
时![]() ,
,![]()
当k=3时也符合上式![]() .......................................................... 10分
.......................................................... 10分
(3)作差得:![]()
其中![]()
由于![]() ,
,![]()
![]()
![]()
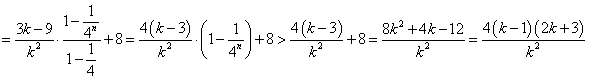 当
当![]() 时
时![]()
原式得证............................................................................................................... 14分。

 题号
题号