08高考文科数学第一次教学质量检测
数学文科
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。共150分。考试时间120分钟。
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率![]()
球的表面积公式![]() ,其中R表示球的半径
,其中R表示球的半径
球的体积公式![]() ,其中R表示球的半径
,其中R表示球的半径
第Ⅰ卷选择题(共55分)
一、选择题:本大题共11小题,每小题5分,共55分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集![]() ,集合
,集合![]() ,则
,则![]()
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]()
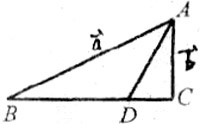 2.如图,已知
2.如图,已知![]() ,用
,用![]() 表示
表示![]() ,则
,则![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知角![]() 在第一象限且
在第一象限且![]() ,则
,则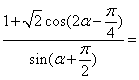
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.把直线![]() 按向量
按向量![]() 平移后恰与
平移后恰与![]() 相切,则实数
相切,则实数![]() 的值为
的值为
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
5.下面命题正确的是
A.已知直线![]() ,点
,点![]() ,直线
,直线![]() ,则
,则![]() 与
与![]() 异面
异面
B.已知直线![]() ,直线
,直线![]() ,则
,则![]()
C.已知平面![]() ,直线
,直线![]() ,直线
,直线![]() ,则
,则![]()
D.若直线![]() 与
与![]() 所成的角相等,则
所成的角相等,则![]()
6.等比数列![]() 中,“
中,“![]() ”是“
”是“![]() ”的
”的
A.充分而不必要条件 B.充要条件
C.必要而不充分条件 D.既不充分又不必要条件
7.已知双曲线![]() 满足彖件:(1)焦点为
满足彖件:(1)焦点为![]() ;(2)离心率为
;(2)离心率为![]() ,求得双曲线
,求得双曲线![]() 的方程为
的方程为![]() 。若去掉条件(2),另加一个条件求得双曲线
。若去掉条件(2),另加一个条件求得双曲线![]() 的方程仍为
的方程仍为![]() ,则下列四个条件中,符合添加的条件共有
,则下列四个条件中,符合添加的条件共有
①双曲线![]() 上的任意点
上的任意点![]() 都满足
都满足![]() ;
;
②双曲线![]() 的—条准线为
的—条准线为![]()
③双曲线![]() 上的点
上的点![]() 到左焦点的距离与到右准线的距离比为
到左焦点的距离与到右准线的距离比为![]()
④双曲线双曲线![]() 的渐近线方程为
的渐近线方程为![]()
A.1个 B.2个 C.3个 D.4个
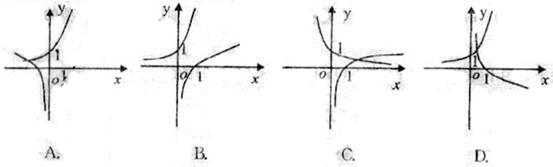
8.已知![]() ,函数
,函数![]() 与函数
与函数![]() 的图象可能是
的图象可能是
9.有两排座位,前排4个座位,后排5个座位,现安排2人就坐,并且这2人不相邻(一前一后也枧为不相邻),那么不同坐法的种数是
A.18 B.26 C.29 D.58
10.偶函数![]() 的定义域为
的定义域为![]() ,若
,若![]() ,且在
,且在![]() 上为单调增函数,则下列命题中的假命题是
上为单调增函数,则下列命题中的假命题是
A.![]() 的图象关于y轴对称 B.
的图象关于y轴对称 B.![]() 为周期函数
为周期函数
C.![]() 在区间
在区间![]() 上是增函数 D.
上是增函数 D.![]() 的图象关于直线
的图象关于直线![]() 对称
对称
11.集合![]() ,集合
,集合![]() 。先后掷两颗骰子,设掷第—颗骰子得点数记作
。先后掷两颗骰子,设掷第—颗骰子得点数记作![]() ,掷第二颗骰子得点数记作
,掷第二颗骰子得点数记作![]() ,则
,则![]() 的概率等于
的概率等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共95分)
二、填空题:(共4题.每题4分,满分16分)
12.![]() 的展开式中的常数项为
的展开式中的常数项为
13.关于![]() 的不等式
的不等式![]() 的解集为
的解集为
 14.已知函数
14.已知函数![]() ,则
,则![]()
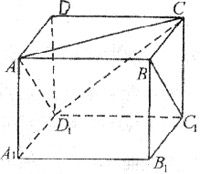
15.如图,正方体![]() ,则下列四个命题:
,则下列四个命题:
①![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积不变;
的体积不变;
②![]() 在直线
在直线![]() 上运动时,直线AP与平面ACD1所成角的大小不变;
上运动时,直线AP与平面ACD1所成角的大小不变;
③![]() 在直线
在直线![]() 上运动时,二面角
上运动时,二面角![]() 的大小不变;
的大小不变;
④M是平面![]() 上到点D和
上到点D和![]() 距离相等的点,则M点的轨迹是过
距离相等的点,则M点的轨迹是过![]() 点的直线
点的直线
其中真命题的编号是 (写出所有真命题的编号)
三、解答题(共6题,满分79分)
16.(12分)
已知函数![]()
(1)求函数![]() 的周期、对称轴方程;
的周期、对称轴方程;
(2)求函数![]() 单调增区间。
单调增区间。
17.(14分)
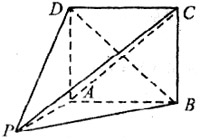
如图,在几何体![]() 中,面
中,面![]() 为矩形,
为矩形,![]() 面
面![]() ,
,![]()
(1)求证;当![]() 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;
(2)当![]() 时,求二面角
时,求二面角![]() 的取值范围。
的取值范围。
18.(12分)
已知椭圆C的中心在原点,对称轴为坐标轴,且过![]() 、
、![]() 。
。
(1)求椭圆C的方程;
(2)设过![]() 的直线
的直线![]() 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求![]() 的取值范围
的取值范围
19.(13分)
食品监管部门要对某品牌食品四项质量指标在进入市场前进行严格的检测,并规定四项指标中只要第四项不合格或其它三项指标中只要有两项不合格,这种品牌的食品就不能上市。巳知每项指标检测是相互独立的。若第四项不合格的概率为![]() ,且其它三项指标出现不合格的概率均是
,且其它三项指标出现不合格的概率均是![]()
(1)若食品监管部门要对其四项质量指标依次进行严格的检测,求恰好在第三项指标检测结束时,能确定该食品不能上市的概率;
(2)求该品牌的食品能上市的概率。
20.(14分)
函数![]() 在
在![]() 处取得极值,其图象在
处取得极值,其图象在![]() 的切线与直线
的切线与直线![]() 垂直。
垂直。
(1)求![]() 的值;
的值;
(2)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围。
的取值范围。
21.(14分)
巳知数列![]() 中,
中,![]()
(1)求![]() ;
;
(2)求证:数列![]() 与
与![]() 都是等比数列;
都是等比数列;
(3)求数列![]() 前
前![]() 的和
的和![]() 。
。
参考答案
一、选择题
1.A 2.B 3.C 4.C 5.C 6.B 7.B 8.C 9.D 10.C
11.B
二、填空题
12.15 13.![]() 14.2007 15.①③④
14.2007 15.①③④
三、解答题
16.![]() 3分
3分
(1)![]() 的周期
的周期![]() ,函数
,函数![]() 对称轴方程为
对称轴方程为![]() ; 6分
; 6分
(2)由![]() 得
得![]()
∴求函数![]() 单调增区间为
单调增区间为![]() 。 12分
。 12分
17.以A为坐标原点,射线AP、AB、AD分别为x轴、y轴、z轴的正半轴建立如图所示的坐标系。设![]() ,
,
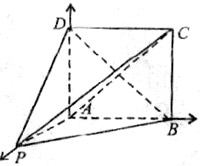 由已知得
由已知得![]()
(1)当![]() 时,
时,![]() ,
,
∴![]() 4分
4分
∴![]() ,∴
,∴![]()
又![]() ,∴平面PBD⊥平面PAC; 6分
,∴平面PBD⊥平面PAC; 6分
解法二:当![]() 时,矩形
时,矩形![]() 为正方形,∴
为正方形,∴![]()
∵![]() 面
面![]() ,∴
,∴![]() 2分
2分
又![]() ,∴BD⊥平面PAC,BD
,∴BD⊥平面PAC,BD![]() 平面PBD,∴平面PBD⊥平面PAC
平面PBD,∴平面PBD⊥平面PAC
(2)设![]() 平面PDB,∴
平面PDB,∴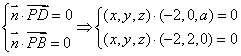
∴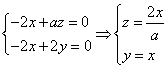
不妨设![]() ,则
,则![]()
设面![]() 的法向量
的法向量![]() 10分
10分
∴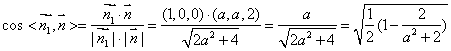
当![]() 变化时,即
变化时,即![]() ,
,![]()
![]() 12分
12分
又![]() ,∴
,∴![]()
经判断二面角![]() 的大小等于
的大小等于![]()
∴二面角![]() 的取值范围是
的取值范围是![]() 14分
14分
(其他解法参照给分)
18.(1)设椭圆![]() 的方程为
的方程为![]() 1分
1分
由椭圆![]() 过
过![]() ,得
,得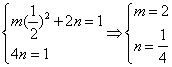 5分
5分
∴椭圆![]() 的方程为
的方程为![]() 6分
6分
(2)当过![]() 的直线
的直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 与曲线
与曲线![]() 无交点,不合题意,
无交点,不合题意,
∴设直线![]() 的方程为:
的方程为:![]() ,
,![]() 与曲线
与曲线![]() 交于
交于![]()
由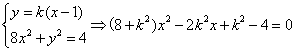
∴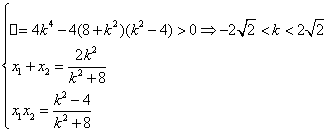
![]()
∴![]()
![]()
![]()
∵![]() ,∴
,∴![]() 的取值范围是
的取值范围是![]() 12分
12分
19.(1)食品监管部门要对其四项质量指标依次进行严格的检测,恰好在第三项指标检测结束时,能确定该食品不能上市的概率等于第一、第二指标中恰有一项不合格而第三项指标不合格的概率。
∴所求概率![]() 6分
6分
(2)该品牌的食品能上市的概率等于1减去该品牌的食品不能上市的概率,
即![]()
解法二:该品牌的食品能上市的概率等于四项指标都合格或第一、第二、第三项指标中仅有一项不合格且第四项指标合格的概率,
即![]() 13分
13分
20.(1)![]()
由题意得![]() ,解得
,解得![]() 6分
6分
(2)当![]() 时,
时,![]() 恒成立
恒成立
![]() 当
当![]() 时,
时,![]() 恒成立
恒成立
令![]() ,则
,则![]()
![]() 在
在![]() 是增函数,
是增函数,![]() 是减函数 12分
是减函数 12分
而![]() ,所以当
,所以当![]() 时,
时,![]()
故![]() 14分
14分
21.(1)由![]() 得
得![]()
∴![]() ;∴
;∴![]() ;∴
;∴![]()
4分
(2)∵![]() ,∴
,∴![]()
∴数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列;
为公比的等比数列;
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列。 9分
为公比的等比数列。 9分
(3)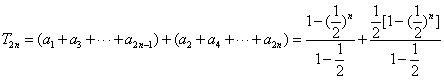
![]() 14分
14分