专题考案(2)数列板块 测试
第Ⅰ卷 (选择题 共60分)
一、选择题(12×5′＝60′)
1.{
}为等差数列，
为其前n项和，
<
,=
>
,则下列错误的是 （ ）
A.d<0 B.
=0
C.
> D.和均为的最大值
2.设α、β是方程
的两根，且α、α+β、β成等比数列,则k的值为 ( )
A.2 B.4 C.±4 D.±2
3.在等比数列{}中，
(a≠0)，
，则
等于 ( )
A.
B.
C.
D.
4.已知{}是递增数列，且对任意n∈N*，都有
恒成立， 则实数γ的取值范围是( )
A.γ>0 B.γ<0 C.γ＝０ D.γ>-3
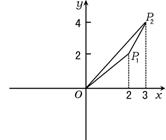
5.在直角坐标系中，O为坐标原点，
(
,
)，
（
，
）是第一象限的两个点，若1，，，4依次成等差数列，而1，,，8依次成等比数列，则
的面积是 ( )
A.1 B.2 C.3 D.4
6.在等差数列{}中，若＝18，=240,-4＝30，则n的值为 ( )
A.14 B.15 C.16 D.17
7.一个等比数列的前n项之和是
，那么它的前n项的各项平方之和为 ( )
A.
B.
C.
D.
8.设x、
、
、y成等差数列，x、
、
、y成等比数列，则
的取值范围是 ( )
A.
4，＋∞)
B.(-∞,0
∪4，＋∞)
C.0,4）
D.(－∞,-4)∪4,＋∞)
9.首项为31，公差为-6的等差数列{}中，前n项和为,则数列{}中与零最近的项是( )
A.第9项 B.第10项 C.第11项 D.第12项
10.等差数列{}中,
,
(p≠q),则
的值是 ( )
A.大于4 B.小于4 C.等于4 D.不能确定
11.等差数列｛｝的首项
，前n项的和为，若
(m、k∈N*且m≠k)，则取最大值是 ( )
A.
n=
B.n=
C.当m+k为偶数时，n=；当m+k为奇数时，n=
D.当m+k为偶数时，n=；当m+k为奇数时，n=
12.数列｛｝中任何相邻两项x、y满足
(x,y≠0)，那么此数列是 ( )
A.等差数列 B.等差或等比数列 C.等比数列 D.以上答案都不对
第Ⅱ卷 (非选择题 共90分)
二、填空题(4×4′＝16′)
13.无穷数列{}同时满足条件：
①对任意自然数n∈N*,都有-2<<4;
②当n为正偶数时，
<,且>
;
③当n>3时，>0.
请写出一个满足条件的{}的通项公式
.
14.三角形的三边长构成等比数列，那么公比q的取值范围是 .
15.在公差为d的等差数列{}中有“
,
,…,
+…+
,…(m、k∈N*)构成公差为
的等差数列”,像这样在公比为q的等比数列{
}中有
.
16.一个等比数列｛｝，
，前11项的几何平均数是32，若从前11项抽出一项后的几何平均数是16，则抽出的是第
项.
三、解答题(5×12′+14′＝74′)
17.已知f (x)是定义域在自然数集上的函数，当x为奇数时，有f (x+1)-f (x)=1，当x为偶数时，有f (x+1)-f (x)=3,且f (1)+f (2)=5.
(1)求证：f (1)，f (3)，…，f (2n-1)(n∈N*)成等差数列；
(2)求f (n)的解析式.
18.数列{}中，=8,
=2,且满足
(n∈N*).
(1)求数列{}的通项公式;
(2)设=++…+，求;
(3)设=
(n∈N*),
(n∈N*),是否存在最大的整数m,使得对任意n∈N*,均有
成立？若存在，求出m的值;若不存在，请说明理由.
19.数列{}满足=1,当n∈N*,且n≥2时，
.
(1)当n≥2时，求证：
;
(2)比较（1+
）(1+
)(1+
)…(1+
)与4的大小关系.
20.某人2000年元月存款t元，按年利息为p的复利计息.计划从2001年开始，每年元月1号到银行提取确定的金额供子女上学使用，恰好在n年后取完.求该人每年提取的金额.
21.对负整数a,数
、6a+6、10a+3可构成等差数列.
(1)求a值;
(2)若数列{}满足
(n∈N*),首项为
.
①令
,求{}的通项公式;
②若对任意n∈N*有
,求的取值范围.
22.已知数列{}的通项公式是=
(n=1,2,…),是否存在非零常数p和q,使数列{
}成等差数列?若存在，求出p和q满足的关系式；若不存在，说明理由.
参考答案
1.C ∵
,∴
,
∵
,∴
,
,
又
,∴
,有d<0,,
故A、B正确，对C，
,
∴
,对数列{},
>…
故D项正确.
2.D ∵α+β=2,αβ=
,又αβ=
,∴
,∴k=±2,故选D.
3.A 依题意，数列:
，
，
，…，，…为等比数列，
公比q=
，为该数列的第10项，
故＝a·
，A正确.
4.D 依题意，
恒成立，
.
则2n+1+γ>0
γ>-(2n+1)恒成立，-(2n+1)≤-3，故满足条件的γ的取值范围是γ>-3.
5.A 不难求出
，=3，=2，=4，
|
(2，2)，(3，4)，如图所示，
所在直线
方程为4x-3y=0，于是，△
的边上的高
h=
，又=5，故
＝
×5×
=1.
6.B 
，
故n=15.
7.D 设该等比数列的前n项和为，则
，故
,
故
，则
8.B 依题意，
，
，则
.
又
≥2xy，若xy>0，则≥2xy，于是
≥
，
故≥4，当且仅当x=y时取“=”号；若xy<0，
则≥-2xy，于是≤
，
故≤0，当且仅当x=-y时取“=”号.综上所述，
的取值范围是(-∞，0∪4，+∞).
9.C 
,∴=31n-3n(n-1).
令31n-3n(n-1)=0,得n=11.333.又∵n为整数，取n=11或12,
当n=11时，=11,当n=12时，=-24.∴前11项的和
距0最近.
点评 本题是考查等差数列的前n项和公式，注意n是整数，于是要考虑较近的整数.
10.A ∵=
>4,故选A.
11.D 方法1 由
(m≠k)，
由，知d<0.
=
.
|
时，取最大值；
当m+k为奇数时，n=时，取最大值.
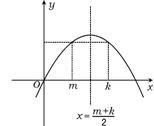
方法2 依题意，d<0，如图所示，(n,)表示抛物线上的
一些离散点，此抛物线的对称轴方程x=,则当m+k
为偶数时，n=时取最大值；m+k为奇数时，
n=时取最大值.
12.D 
x=2y或x-y=1，不妨取
，
，
=…=0.
|
;
;…
点评 本题是一道开放性试题，答案是不惟一的.解本题要根据题设:∈(-2,4),而是n的一个函数式，即说明函数的值域为(-2,4).于是我们就想到了三角函数（正弦函数或余弦函数等等）.再由
，且
(n为正偶数)，说明偶数项比奇数项大，联想到波动函数.由条件③知随n增大，>0,这可能与
有关.于是就构造出给出的几个表达式.
14.(
，
) 依题意，设该三角形的三边长分别为a、aq、
，当q≥1时，a+aq>1+q>
1≤q<；当0<q<1时，+aq>a+q>1<q<1.综上可知，q∈(，).
15.
…
,
…
,…,
…
,…构成公比为
的等比数列.
16.11 设抽出的是第k项，依题意
，
，于是有
.
由
，即
q＝
.
2k-7=15 k=11.
17.解 (1)当x为奇数时，x+1为偶数，代入已知等式有
f (x+1)-f (x)=1 ① f (x+2)-f (x+1)=3. ②
①+②得:f (x+2)-f (x)=4为常数.又
∴f (1),f (3),f (5)，…，f (2n-1)构成以首项为2、公差为4的等差数列.
(2)由②知:当n为奇数时，f (n+2)-f (n)=4，f (1)=2，
∴当n=2k-1时，f (n)=f (2k-1)＝2+(k-1)×4＝2n.
当n为偶数时，n+1为奇数，f (n+1)-f (n)=3，f (n+2)-f (n+1)=1f (n+2)-f (n)=4，
∴f (2),f (4),f (6)，…,f (2n)构成首项为3、公差为4的等差数列.
∴当n=2k时，f (n)=f (2k)=3+(k-1)×4＝2n-1.
|
18.解 (1)由知，数列{}为等差数列，设其公差为d,则d=
,
故
.
(2)由
≥0,解得n≤5.故
当n≤5时，=++…+=++…+=
;
当n>5时，=++…+=++…+
-…-=
.
(3)由于=
,
所以
,
从而
>0.
故数列
是单调递增的数列，又因
是数列中的最小项，要使恒成立，则只需
成立即可，由此解得m<8,由于m∈Z,故适合条件的m的最大值为7.
19.(1)证明 当n≥2时,有
,
则可得
,
∴.
(2)当n=1,2时，易知1+=2<4,(1+)(1+
)=2×
<4.
由（1）知，当n≥2时，有
,化为
;
当n≥3时，(1+)(1+)(1+)…(1+)=
=
=2·
·
·
…
·(1+)
=
=
.
∵
(n≥2),
∴(1+)(1+)(1+)…(1+)<
［1+(1-)+(-
)+…+(
-
)］
=(2-)=4+
-
<4+-<4+-
-=4-<4.
∴当n
N*，有(1+)(1+)(1+)…(1+)<4.
20.解 设该人每年取款x元，则
,
…
由此可归纳出
.
此时只需令=0，便得x=
.
答:此人每年的取款金额是.
21.解 (1)∵
,∴
,a=-2或a=3而a<0,且a∈Z,∴a=-2.
(2)①
,
∴
,
,
∴
.
②
,即
(n∈N*)
而
,∴4(2n+1+)>2n-1+,>-2n-
,n∈N*,
∴>-2-=-
.
22.解 假设存在非零常数p和q，使数列{}成等差数列,令
=,即=
,
数列{}的公差为d,则=
+(n-1)d=dn+(-d).由=dn+(-d),整理得
.
此式对任意n∈N*都成立.故dp=2,dq+p(-d)=-1,q(-d)=0.
由于q≠0,故-d=0,∴dp=2,dq=-1,得p=-2q.
故存在非零常数p和q，满足p=-2q时，{}为等差数列.