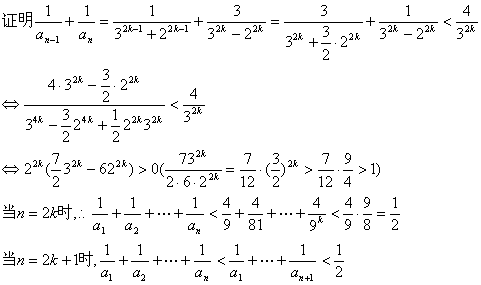08届高三理科数学第一学期期末考试
一、选择题：（每小题5分，满分60分）
1．已知集合
的真子集，则实数a的取值个数是 （ ）
A．0个 B．1个 C．3个 D．无数个
2．已知
等于 （ ）
A．
B．
C．
D．
3．已知向量
方向上的投影为 （ ）
A．
B．
C．—2 D．2
4．若
的最小值为 （ ）
A．9 B．
C．
D．
5．设等比数列
，若S10：S5=1：2，则S15：S5= （ ）
A．3：4 B．2：3 C．1：2 D．1：3
6．设直线m，n和平面
，对下列命题：
（1）若
；
（2）若
所成角的大小也为
；
（3）若
；
（4）若
上的射影为两条直交直线，其中正确命题的个数为 （ ）
A．2个 B．1个 C．3个 D．4个
7．设函数
上不是单调函数的充要条件是
（ ）
A．
B．
C．
D．
8．设O在△ABC内部，且
，则△ABC的面积与△AOC的面积之比是
（ ）
A．3 B．4 C．5 D．6
9．把函数
平移所得的图象关于y轴对称，则m的最小值为 （ ）
A．
B．
C．
D．
10．已知数列
的前三项依次是—2，2，6，前n项的和Sn是n的二次函数，则a100等于
|
A．3900 B．392 C．394 D．396
11．函数
的定义域为R，对任意实数x满足
当
（ ）
A．
B．
C．
D．
12．设定义在R上的函数
，则
等于 （ ）
A．0 B．—2 C．2 D．2x—4
二、填空题：（每小题5分，满分20分）
13．若
= 。
14．已知
=
。
15．在△ABC中，角A，B，C所对的边分别是a，b，c，若
，则△ABC的面积等于
。
16．将正整数按下表的规律排列，把行与列交叉处的一个数称为某行某列的数，记作 
，如第2行第4列的数是15，记作
是
。
1 4 5 16 17 36 ……
2 3 6 15 18 35 ……
9 8 7 14 19 34 ……
10 11 12 13 20 33 ……
25 24 23 22 21 32 ……
26 27 28 29 30 31 ……
…… …… …… …… ……
三、解答题：（本大题共6小题，满分70分）
17．（满分10分）
设向量
，
的值。
18．（满分12分）
已知a为实数，
（1）若
在[—4，4]上的最大值和最小值；
（2）若
上都是递增的，求a的取值范围。
19．（满分12分）
已知数列
（1）求数列
；
（2）设
20．（满分12分）
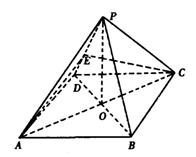
如图，正方形ABCD中，
，点E在PD上，PE：ED=2：1。
（1）证明：PD⊥平面EAC；
|
（3）求点B到平面PDC的距离。
21．（满分12分）
已知二次函数
（1）求
的值；
（2）数列
，若对任意的实数
，其中
是定义在实数集R上的一个函数，求数列的通项公式；
（3）设圆
是各项都是正数的等比数列，设
个圆的面积之和，求
22．（满分12分）
已知数列
（1）求出所有使数列
值，并说明理由；
（2）求数列的通项公式；
（3）求证：
参考答案
一、选择题
1．D 2．B 3．D 4．C 5．A 6．B 7．B 8．B 9．B 10．C 11．A 12．A
|
|
13．
14．—8 15．
16．（63，53）
三、解答题
17．
18．（1）
| x | (—∞,－1) | —1 |
|
|
|
|
| + | 0 | — | 0 | + |
|
| 增 | 极大 | 减 | 极小 | 增 |
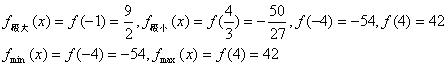
（2）
均成立，
19．（1）
（2）
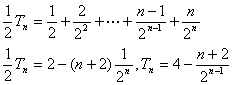
20．（1）
（2）∠CEA为二面角A—PD—C的平面角，
（3）点B到平面PDC的距离为
21．（1）
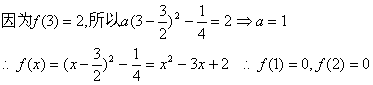
（2）令
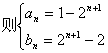
（3）
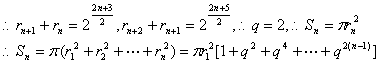
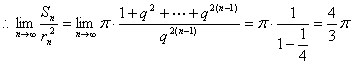
22．（1）
（2）
（3）当
时，
