高考数学三角函数的最值测试

专题考案(3)三角板块 第4课 三角函数的最值

(时间：90分钟　满分：100分)

题型示例

已知f(x)=4msinx-cos2x(x∈R).若f(x)的最大值为3，求实数m的值.

分析　将sinx整体代换成变量t，通过学习过的正弦函数的值域赋予变量t的取值范围，再运用二次函数的理论求得满足题意的结果.

解f(x)=4msinx-cos2x=2sin²x+4msinx-1=2(sinx+m)²-(2m²+1),令t=sinx,则f(x)可化为g(t)=2(t+m)²-(2m²+1)(-1≤t≤1).

①当-m≤0时，则在t=1处,f(x)_max=1+4m, 由得m=;

②当-m>0时，则在t=-1处，f(x)_max=1-4m,由;综上，m=±.

点评　本题主要考查三角函数的值域问题和二次函数的值域问题.

一、选择题(9×3′＝27′)

1．函数y=2sinxsin2x的最大值是　　　　　　　　　　  　　　　　　　　　　 (　　)

A .　　　　B.　　  C.　　  D.

2．若函数y=1-2cosx-2sin²x的值域为［a,b］，则b²+4a的值为　　　　　　　　  (　　)

A.1　　　　  B.2　　　　  C.3　　　　  D.4

3．函数y=(sin²x+csc²x)+(cos²x+sec²x)的最小值是　　　　　　　　　　　　　　 (　　)

A.4　　　　  B.3　　　　  C.5　　　　  D.不存在

4．函数y=cos2x+3sinx的最小值与最大值分别是　　　　　　　　　　　　　　 (　　)

A.-4,4　　  B.,4　　　 C.-4, 　　　 D-,

5．函数y=log₂(1+sinx)+log₂(1-sinx)，当x∈［-,］时的值域为　　　　　　  (　　)

A.［-1,0］　　 B.(-1,　　 C.［0,1］　　 D.［0,1］

6．函数f(x)=sin(-x)·sin(+2x)·cos(π+x)的最大值和最小值分别为　　　 (　　)

A.,- 　　　B,-　　　 C.1,-1　　　 D.1,0

7．函数y=x,x∈［-1,1］的最大值、最小值分别是　　　　　　　　　　 (　　)

A .1，0　　　 B.1,-1　　　 C.，-　　　 D，0

8．函数y=+sin²x(x≠kπ,k∈Z)的值域是　　　　　　　　　　　　　　  ( 　 )

A.［2,+　　  B.(1,2　　  C.(0,　　  D.［4,+∞］

9．当0<x<时，函数f(x)=的最小值是　　　　　　　　　   (　　)

A.　　　　  B.　　　　  C.2　　　　  D.4

二、填空题(4×3′＝12′)

10．y=sin(x-)cosx的最大值是　　　　，最小值是　　　　.

11．函数y=2sin(kx-)的周期为T,且T∈(1,3)，则正整数k的最大值是　　　　.

12．函数f(x)=的最大值和最小值分别为　　　　 和　　　　.

13．已知函数y=acosx+b的最大值为1，最小值为-7,则acosx+bsinx的最大值是　　　　.

三、解答题(7′＋3×8′＋10′＝41′)

14．求函数f(x)=的最小正周期，最大值和最小值.

15．求下列函数的最值：

(1)y=2sec²x+cot⁴x.

(2)y=(1+cosx)·sin(0<x<π).

16．求函数y=sinx·cosx+a(sinx+cosx)的最值.

17．在△ABC中，角A、B、C所对的边分别为a、b、c,且cosA=.

(1)求sin²+cos2A的值;

(2)若a=,求bc的最大值.

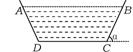
18．欲修建一横断面为等腰梯形(如图1)的水渠，为降低成本必须尽

图1

量减少水与渠壁的接触面，若水渠横断面面积设计为定值S，渠深h，

则水渠壁的倾角α(0<α<90)应为多大时，方能使修建成本最低?

四、思考与讨论 (2×10′＝20′)

19．求函数y=+sinx的值域.

20．记x的函数y=1-2a-2acosx-2sin²x的最小值为f(a),试用a表示f(a).

参考答案

1．A　y=4sin²xcosx=2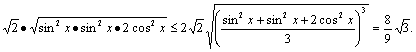

2．C　y=cos2x-2cosx=2cos²x-2cosx-1=2(cosx-)²-.

当cosx=时,y_min=-=a;当cosx=-1时,y_max=3=b.∴b²+4a=9+4×(-)=3.

3．C　y=1+csc²x+sec²x=3+cot²x+tan²x≥3+2=5.

4．C　y=1-2sin²x+3sinx=-2(sinx-)²+.sinx=时，y_max=;sinx=-1时，y_min=-4.

5．A　y=log₂(1-sin²x)=log₂cos²x.x∈［-,］时，cosx∈［,1］，cos²x∈［,1］

∴y∈［-1,0］.

6．A　∵f(x)=cos2x·cosx·(-sinx)=-sin4x,∴最大值和最小值分别为.-.

7．C　设x=sinα,α∈［-,］,则y=sinαcosα=sin2α，2α∈［-π,π］，∴-≤y≤.

8．D　设t=sin²x,t∈(0,1)，y=t+在(0,1］上为减函数，∴y≥1+=4.

9．D　∵0<x<,∴cos²x≠0,∴f(x)=,∴f(x)_min=4,此时，tanx=.

10．;-　y=［sin(2x-)-sin］=sin(2x-)-.y_max=-=,y_min=--=-.

11．6　由题意1<<k<2π,∴k的最大值为6.

12．;-4　由y=,sinx=1时，y_max=;sinx=-1时，y_min=-4.

13．5　acosx+bsinx=sin(x+φ)≤=5.

14．分析　将f(x)化简成y=Asin(ωx+φ)+k形式，再由周期公式T=，及三角函数性质求最值.

解　f(x) ==(1+sinxcosx)=sin2x+.

所以函数f(x)的最小正周期是π,最大值是,最小值是.

点评  本题是一道基础题，难度系数不大，主要考查三角公式的简单变形，化简以及三角函数的周期性和最值性.

15．解　(1)y=2(1+tan²x)+cot⁴x=2+tan²x+tan²x+cot⁴x≥2+=2+3=5，

当且仅当x=nπ±时等号成立(n∈Z),∴y_min=5,无最大值.

(2)∵0<x<π,∴sin>0,y²=4cos⁴·sin²

=2cos²·cos²·2sin²≤2，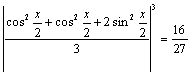

当且仅当tan=时等号成立，∴y≤，即y_max=,无最小值.

16．解　设sinx+cosx=t,则sinx·cosx=(t²-1),t=sinx+cosx=sin(x+)∈［-,］,

y=(t²-1)+at=t²+at-=(t+a)²-a²-(t∈［-,］)

(1)若-a<-,即a>时

当t=-时,y_min=-a+;当t=时,y_max=a+;

(2)若-≤-a≤0即0≤a≤时

当t=-a时,y_min=-a²-;当t=时,y_max=a+;

(3)若0<-a≤,即-≤a<0时

当t=-a时,y_min=-a²-;当t=-时y_max=-a+;

(4)若-a>,即a<-时

当t=时,y_min=a+;当t=-时,y_max=-a+.

点评　一个看似简单的题目，讨论却很繁琐，本题将三角函数与二次函数结合，是三角函数中经常命题的一种方式，值得注意.

17．分析　（1）分别用降幂公式、二倍角公式，化简所求式子再求值.

(2)三角形中出现bc联想用余弦定理解题.

解　（1）sin²+cos2A=［1-cos(B+C)］+(2cos²A-1)

=(1+cosA)+(2cos²A-1)=(1+)+ (-1)=-.

(2)∵=cosA=,∴bc=b²+c²-a²≥2bc-a².∴bc≤a²,

又∵a=,∴(bc)_max=.

当且仅当b=c=时，bc=,故bc的最大值是.

点评　本题通过以三角函数为载体，考查了三角函数的诱导公式、倍角公式、余弦定理等知识，更以三角函数为载体考查了均值不等式，以及考查了学生的运算能力.

18．解　作BE⊥DC于E(图略)，在Rt△BEC中，BC=,CE=hcotα，又AB-CD=2CE=2hcotα,AB+CD=,故CD=-hcotα.

设y=AD+DC+BC,则y= (0°<α<90°)，由于S与h是常量，欲使y最小，只需u=取最小值，u可看作(0，2)与(-sinα,cosα)两点连线的斜率，由于α∈(0°,90°),点(-sinα,cosα)在曲线x²+y²=1(-1<x<0,0<y<1)上运动，当过(0，2)的直线与曲线相切时，直线斜率最小，此时切点为(-，)，则有sinα=,且cosα=，那么α=60°，故当α=60°时，修建成本最低.

19．解　设t=sinx，则有t∈［0, ］，故y=+t.

由于t∈［0, ］,令t=sinθ,θ∈［0, ］,∴y=+sinθ=sin(θ+).

∵θ∈［0, ］，θ+∈［,π］，∴sin(θ+)∈［,1］．

∴sin(θ+)∈[,].∴原函数的值域为［，］．

20．解　y=1-2a-2acosx-2sin²x=1-2a-2acosx-2(1-cos²x)=2(cosx-)²--2a-1

（-2≤a≤2） （a>2） （a<-2）

∴f(a)=