08高考文科数学调研考试试题
说明：本试卷分第I卷（选择题）和第II卷（非选择题）两部分. 答题时间120分钟，满分150分.
第I卷（选择题 共60分）
注意事项：
1．答第I卷前，考生务必用蓝、黑色墨水笔将姓名、考试证号填写在答题卡上，并用2B铅笔在答题卡上规定位置涂黑自己的考试证号和考试科目.
2．每小题选出答案后，用铅笔涂黑答题卡上对应题目的答案标号. 如需改动，用橡皮擦干净后，再选涂其它答案。答案写在试题卷上无效。
一、选择题（本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的）
1．若A、B、C是三个集合，则“A∩B=C∩B”是“A=C”的 （ ）
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．既非充分又非必要条件
2．要得到函数
）的图象，可以将函数
的图象 （ ）
A．向右平移
个单位长度 B．向左平移个单位长度
C．向右平移
个单位长度 D．向左平移个单位长度
3．等差数列
的中，若
（ ）
A．1 B．3 C．4 D．5
4．已知圆
，则过原点且与C相切的直线方程为 （ ）
A．
B．
C．
D．
5．若x，y为非零实数，且x<y，则下列不等式成立的是 （ ）
A．
B．
C．
D．
6．函数
的反函数为 （ ）
A．
B．
C．
D．
7．已知实数x，y满足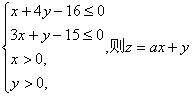
的最大值为7，则a的值为 （ ）
A．1 B．－1 C．
D．－
8．函数
的最小正周期为π，则正数
的值为 （ ）
A．4 B．2 C．
D．1
9．下列函数中既是偶函数，又是区间[－1，0]上的减函数的是 （ ）
A．
B．
C．
D．
|
上一点A到右焦点的距离为2，则A到左准线的距离为 （ ）
A．
B．
C．4 D．8
11．若函数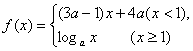
对任意
，都有
<0，则a的取值范围是 （ ）
A．（0，1） B．（0，
） C．（
D．
|
为n阶幻方对角线上的数的和，如右表就是一个3阶幻方，且
，则等于（ ）
A．
B．
C．
D．
第II卷（非选择题 共90分）
|
1．用钢笔或圆珠笔直接答在试题答中。
2．答卷前将密封线内项目填写清楚。
二、填空题（本大题共4小题，每小题5分，共20分.把答案填在题中的横线上）
13．若直线
平行，则m的值为
.
14．抛物线
的焦点坐标为
.
15．若△ABC的内角A满足
，则
.
16．若点D在△ABC的边BC上，
的值为
.
三、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）
17．（本小题满分10分）
设
，解关于x的不等式
18．（本小题满分12分）
在锐角三角形ABC中，角A、B、C的对边分别为a、b、c. 向量u=
v=
u⊥v.
（I）求角B；
（II）求
的最大值.
19．（本小题满分12分）
已知函数
在区间[－1，2]上是减函数，求
的最大值.
20．（本小题满分12分）
已知数列
（I）证明数列
为等差数列；
（II）设
21．（本小题满分12分）
已知函数
（I）当a>2时，求函数
的极小值；
（II）讨论曲线
轴的公共点的个数.
22．（本小题满分12分）
已知椭圆的中心在原点，对称轴为坐标轴，其左焦点为F，长轴长为4，左顶点到左准线的距离与左顶点到左焦点的距离之比为2
，过F点倾斜角为
）的直线l与椭圆交于P、Q两点，直线OP、OQ分别交左准线于M、N.
（I）求椭圆的方程；
（II）求
的取值范围.
参考答案
一、选择题（本大题共12小题，每小题5分，共60分）
1．B 2．A 3．A 4．C 5．C 6．C 7．A 8．D 9．D 10．D 11．D 12．B
|
13．1 14．（2，0） 15．
16．0
三、解答题（本大题共6小题，共70分）
17．（本小题满分10分）
解：①当
时，不等式为
，解集为（－∞，0）；……………………2分
②当
，解集为（－∞，－a）
；……………………5分
③当a=1时，不等式为
；……………………7分
④当a>1时，
…………………………………10分
18．（本小题满分12分）
解：（I）∵u⊥v，∴u·v=0，即
……3分
又
……………………………………………………………………6分
（II）由（I）知
………………………………………………………………9分
又
∴当A－=0，即A= 时，的最大值为
……………………12分
19．（本小题满分12分）
解：由题意，
在区间[－1，2]上满足
恒成立，………2分
则
……………………………………………………5分
此问题相当于在约束条件
下………………………………8分
求目标函数
的最大值.
作可行域图，由图可知，当直线
，过点M时，p最大.（图略）
由
得
…………………………………………12分
20．（本小题满分12分）
解（I）
，
…………………………3分
由题意，
是首项为1，公差为2的等差数列.……………………………………6分
（II）由（I）知
……………………8分
……………………10分
…………………………………………12分
21．（本小题满分12分）
解：（I）
……………………2分
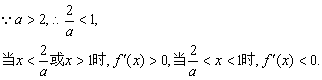
……………………………………………………4分
（II）①
；…………5分
②
∴曲线与x轴有三个公共点.………………………………………………7分
③当
∴曲线与x轴有一个公共点.………………………………………………9分
④当
曲线与x轴只有一个公共点.…………10分
⑤当
，
∴曲线与x轴有一个公共点.…………………………………………………11分
综上所述，时，曲线与x轴有一个公共点；
时，曲线与x轴有三个公共点.…………………………………………12分
22．（本小题满分12分）
解：（I）设椭圆方程为
则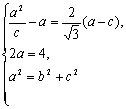
……………………………………3分
解得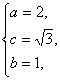
∴椭圆方程为
……………………6分
（II）设直线
整理，得
则
.………………………………………………………………8分
又
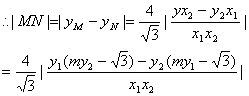
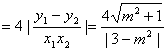，………………………………………………10分
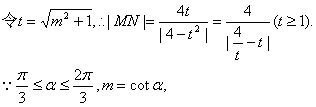
……11分
上递减，
…………………………………………12分
另解：
（II）当
时，直线l与椭圆左准线平行，不存在M、N点；…………7分
当
，
设
，…………9分
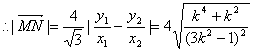，……………………………………10分
令
由
……………………………………11分
……………………………………………………………12分