08高考理科数学二月月考试题

08高考理科数学二月月考试题

数学试题（理科）

考试时间：120分钟　 满分：150　　考试内容：全部

一、选择题(本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.)

1．复数在复平面中所对应的点到原点的距离为

　 A．　　　　　　　　　　 　 B．　　　　　　　　　　 C．1　　　　　　　 　 D．

2．设集合，则下列关系中不正确的是

　 A．　　　　 　 B．　　　　 　 C．　　　　　　　　　　 　 D．

3．给出两个命题：p: x=x的充要条件是x为正实数；q: 存在反函数的函数一定是单调函数.则下列复合命题中的真命题是

　 A．p且q　　　　　　　　　 B．p或q　　　　　　　　　 C．┓p且q　　　　　　　 D．┓p或q

4．设向量与的模分别为6和5，夹角为120°，则等于

　 A．　　　　　　　　　　 　 B．　　　　　　　　　 　 C．　　　　　　　　 　 D．

5．若的展开式中的系数是80，则实数a的值为

　 A．-2　　　　　　　　　　 　 B．　　　　　　　　 　 C．　　　　　　　　　 　 D．2

6．已知函数f(x)是定义在R上的奇函数，当x<0时，，那么的值为

　 A．3　　　　　　　　　　　　 B．-3　　　　　　　　　　 　 C．2　　　　　　　　　　　　 D．-2

7．若国际研究小组由来自3个国家的20人组成，其中A国10人，B国6人，C国4人，按　　　 分层抽样法从中选10人组成联络小组，则不同的选法有（　 ）种.

　 A．　　　　　　　　　　 B．　　　　　 　 C．　　　　　 　 D．

8．二次函数，当n依次取1，2，3，4，…，n，…时，图象在x轴上截得的线段的长度的总和为

A．1　　　　　　　　　　　 B．2　　　　　　　　　 　　　　 C．3　　　　　　　　　　 　 D．4

9．平面、、两两互相垂直，点，点A到、的距离都是3，P是上的动点，P到的距离是到点A距离的2倍，则点P的轨迹上的点到的距离的最小值是

　 A．　　　　　　　　　　　　　　B．　　　　　　　　　C．　　　　　　　　　 D．

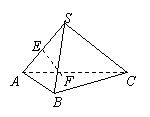
10．如图，在正四面体S—ABC中，E为SA的中点，F为DABC的

中心，则异面直线EF与AB所成的角是

A．30°　　　　　　　 B．45°　　　　　　　

C．60°　　　　　　　 D．90°

11．已知函数，若实数是方程的解，且，则的值为

　　　 A．恒为正值　　　　　　　 B．等于　　　　　　　　C．恒为负值　　　　　　D．不大于

12．设椭圆，右焦点F（c,0），方程的两个根分别为x₁,x₂，则点P（x₁,x₂）在

　　A．圆内　　　　　　　　 B．圆上

　　C．圆外　　　　　　　　 D．以上三种情况都有可能

答题纸

一、选择题 （将正确答案的代号填入下表内）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题(本大题共4小题，每小题5分，共20分.把答案填在答题卡的相应位置上.)

13．不等式的解集为________________.

14．点P是双曲线的一个交点，且2∠PF₁F₂=∠PF₂F₁，其中F₁、F₂是双曲线C₁的两个焦点，则双曲线C₁的离心率为

　　　　　　　　 .

15．湖面上漂着一个小球，湖水结冰后将球取出，冰面上留下一个直径为12cm，深2cm的空穴，则该球的表面积为_____________cm².（）

16．直线l：过点，若可行域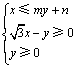的外接圆的直径为，则实数n的值为________________.

三、解答题(本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.)

17．(本小题满分10分)已知向量，记

（1）求f(x)的值域及最小正周期；（2）若，其中，求角

18．(本小题满分12分)设在12个同类型的零件中有2个次品，抽取3次进行检验，每次任取一个，并且取出不再放回，若以表示取出次品的个数. 求的分布列，期望及方差.

 

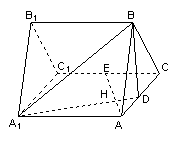19．（本小题满分12分）如图，正三棱柱所有棱长都是，是棱的中点，是棱的中点，交于点

　 （1）求证：；

　 （2）求二面角的大小（用反三角函数表示）；

　 （3）求点到平面的距离.

20．(本小题满分12分)设函数(其中)的图象在处的切线与直线平行.

　　(1)求的值；

(2)求函数在区间[0,1]的最小值；

(3)若,, ,且,

试根据上述(Ⅰ)、(Ⅱ)的结论证明:.

21．（本小题满分12分）已知曲线C上任意一点M到点F（0，1）的距离比它到直线 的距离小1.

　 （1）求曲线C的方程；

　 （2）过点当△AOB的面积为时（O为坐标原点），求的值.

22．（本小题满分12分）在直角坐标平面上有一点列 对一切正整数n，点P_n在函数的图象上，且P_n的横坐标构成以为首项，－1为公差的等差数列{x_n}.

　 （1）求点P_n的坐标；

　 （2）设抛物线列C₁，C₂，C₃，…，C_n，…中的每一条的对称轴都垂直于x轴，抛物线C_n的顶点为P_n，且过点D_n（0，）.记与抛物线C_n相切于点D_n的直线的斜率为k_n，求

　 （3）设等差数列的任一项，其中是中的最大数，，求数列的通项公式.

参考答案

1.B  2.D　3.D　4.D  5.D　6.C　7.D  8.A　9.A　10.C　11.A　 12 A 13.　　　 14. 　15． 　　　 16．8

17．（1）根据条件可知：

　　因为f(x)的定义域为

∴f(x)的值域为，f(x)的最小正周期为

（2）

所以，，又因为，所以

所以

18．的可能值为0，1，2. 若=0表示没有取出次品，其概率为；

同理 ∴的分布为

	0	1	2
p

∴，

19．（1）证明：建立如图所示，

　

∵　　　

∴　　  即AE⊥A₁D，　AE⊥BD　 ∴AE⊥面A₁BD

（2）设面DA₁B的法向量为

由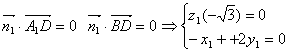　∴取

设面AA₁B的法向量为  ，

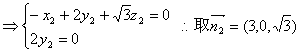由图可知二面角D—BA₁—A为锐角，∴它的大小为arcos　

（3），平面A₁BD的法向量取

则B₁到平面A₁BD的距离d=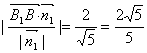

20. (1)因为, 所以　　　

解得m=－1或m=－7(舍),即m=－1　 (2)由,解得

列表如下:

x	0	(0,)		(,1)	1
		－		＋
f(x)	2	↘		↗	2

所以函数在区间[0,1]的最小值为　　

(3)因为　　

由(2)知,当x∈[0,1]时, ,所以,

所以　　　　

当,,,且时, ,,,所以

　 又因为,

　 所以　 故(当且仅当时取等号)　 　

21．（1）的距离小于1，

∴点M在直线l的上方，点M到F（1，0）的距离与它到直线的距离相等，所以曲线C的方程为

　 （2）当直线m的斜率不存在时，它与曲线C只有一个交点，不合题意，

设直线m的方程为，

代入　（*）与曲线C恒有两个不同的交点　　设交点A，B的坐标分别为，

则

点O到直线m的距离，

 ，

（舍去）

当方程（*）的解为　 若

若　当方程（☆）的解为

若

若　所以，

22．（1），

（2）的对称轴垂直于x轴，且顶点为P_n，∴设的方程为

把，∴的方程为

∵∴

∴

=　　（3），

，∴S中最大数a₁=－17.

设公差为d，则a₁₀=由此得　又∵

∴　 ∴，∴