08高考理科数学函数与导数检测题
一、选择题(每小题5分)
1. 函数![]() 的定义域为 ( )
的定义域为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
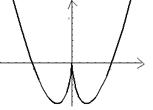
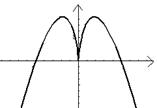 2.函数
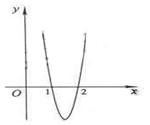
2.函数![]() 的图像是:( )
的图像是:( )
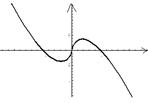
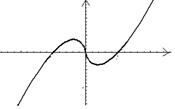
A B C D
3.设![]() 是方程
是方程![]() 的解,则
的解,则![]() 在下列哪个区间内:( )
在下列哪个区间内:( )
A.(3,4) B.(2,3) C.(1,2) D.(0,1)
4.已知![]() (
(![]() 是常数),在
是常数),在![]() 上有最大值3,那么在
上有最大值3,那么在![]() 上的最小值是(
)
上的最小值是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.若曲线![]() 的一条切线
的一条切线![]() 与直线
与直线![]() 垂直,则
垂直,则![]() 的方程为( ) A.
的方程为( ) A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数![]() 的最大值为( )
的最大值为( )
A.![]() B.e
C.
B.e
C.![]() D.10
D.10
7.已知函数![]() 的导数为
的导数为![]() ,且图象过点(0,-5),当函数
,且图象过点(0,-5),当函数![]() 取得极
取得极
大值-5时,x的值应为( )
A. –1 B. 0 C. 1 D. ±1
8.点P在曲线y = x3- x +![]() 上移动时,过点P的切线的倾斜角的取值范围是( )
上移动时,过点P的切线的倾斜角的取值范围是( )
A.
[0,π)
B、(0,![]() )∪[
)∪[![]() ,π)
,π)
C.[0,![]() )∪(
)∪(![]() ,
,![]() ]
D、[0,
]
D、[0,![]() )∪[
)∪[![]() ,π)
,π)
 二、填空题(每题5分,共20分,其中15题第一空2分,第二空3分)
二、填空题(每题5分,共20分,其中15题第一空2分,第二空3分)
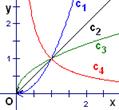
9.如图所示,曲线是幂函数![]() 在第一象限内的图象,
在第一象限内的图象,
已知![]() 分别取
分别取![]() 四个值,则相应图象依次为:
四个值,则相应图象依次为:
 10.函数
10.函数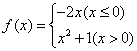 ,则
,则![]() ;若
;若![]() ,则x=
。
,则x=
。
11.点![]() 是曲线
是曲线![]() 上任意一点, 则点
上任意一点, 则点![]() 到直线
到直线![]() 的距离的最小值是
的距离的最小值是
12. 已知函数![]() 在点
在点![]() 处取得极小值,其导函数
处取得极小值,其导函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,如图所示.则
,如图所示.则![]() =
=
13.函数y=x-2sinx在(0, 2![]() )内的单调增区间为
.
)内的单调增区间为
.
14.向高为8m,底面边长为8m的倒置正四棱锥形的容器内注水,其速度为每分钟![]() ,则当水深为5m时,水面上升的速度为
.
,则当水深为5m时,水面上升的速度为
.
三、解答题(共80分)
15.(本小题满分12分)
已知![]()
(Ⅰ)求![]() 的定义域;
(Ⅱ)判断
的定义域;
(Ⅱ)判断![]() 的奇偶性并予以证明;
的奇偶性并予以证明;
(Ⅲ)求使![]() >0的x取值范围.
>0的x取值范围.
16.(本小题12分)
已知曲线y=![]() , (1) 求曲线在点P(1,1)处的切线方程。(2)求曲线过点Q(1,0)的切线方程。(3)求满足斜率为
, (1) 求曲线在点P(1,1)处的切线方程。(2)求曲线过点Q(1,0)的切线方程。(3)求满足斜率为![]() 的曲线的切线方程。
的曲线的切线方程。
17.(本小题14分)
设函数![]()
(Ⅰ)求![]() 的单调区间和极值;(Ⅱ)若关于
的单调区间和极值;(Ⅱ)若关于![]() 的方程
的方程![]() 有3个不同实根,求实数a的取值范围.(Ⅲ)已知当
有3个不同实根,求实数a的取值范围.(Ⅲ)已知当![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
18.(本小题满分14分)
已知函数![]()
![]() 满足条件:①
满足条件:①![]() ;②对一切
;②对一切![]() ,都有
,都有![]() .
.
(Ⅰ)求![]() 、
、![]() 的值;
的值;
(Ⅱ)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上有最小值-5?若存在,请求出实数
上有最小值-5?若存在,请求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
19.(本小题14分)
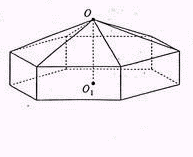
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心![]() 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
 本小题主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力。
本小题主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力。
20.(本小题14分)
已知函数![]() 。
。
(Ⅰ)设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅱ)若对任意![]() 恒有
恒有![]() ,求
,求![]() 的取值范围。
的取值范围。