08高考数学第二轮复习数列练习
一、本章知识结构:
![]()
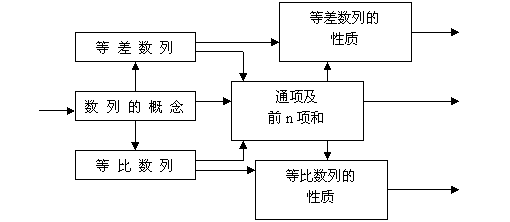
二、高考要求
1. 理解数列的有关概念,了解递推公式是给出数列的一种方法,并能根据递推公式写出数列的前n项.
2. 理解等差(比)数列的概念,掌握等差(比)数列的通项公式与前n项和的公式. 并能运用这些知识来解决一些实际问题.
3. 了解数学归纳法原理,掌握数学归纳法这一证题方法,掌握“归纳—猜想—证明”这一思想方法.
三、热点分析
1.数列在历年高考中都占有较重要的地位,一般情况下都是一个客观性试题加一个解答题,分值占整个试卷的10%左右.客观性试题主要考查等差、等比数列的概念、性质、通项公式、前n项和公式、极限的四则运算法则、无穷递缩等比数列所有项和等内容,对基本的计算技能要求比较高,解答题大多以考查数列内容为主,并涉及到函数、方程、不等式知识的综合性试题,在解题过程中通常用到等价转化,分类讨论等数学思想方法,是属于中高档难度的题目.
2.有关数列题的命题趋势 (1)数列是特殊的函数,而不等式则是深刻认识函数和数列的重要工具,三者的综合求解题是对基础和能力的双重检验,而三者的求证题所显现出的代数推理是近年来高考命题的新热点 (2)数列推理题是新出现的命题热点.以往高考常使用主体几何题来考查逻辑推理能力,近两年在数列题中也加强了推理能力的考查。(3)加强了数列与极限的综合考查题
3.熟练掌握、灵活运用等差、等比数列的性质。等差、等比数列的有关性质在解决数列问题时应用非常广泛,且十分灵活,主动发现题目中隐含的相关性质,往往使运算简洁优美.如a2a4+2a3a5+a4a6=25,可以利用等比数列的性质进行转化:a2a4=a32,a4a6=a52,从而有a32+2aa53+a52=25,即(a3+a5)2=25.
4.对客观题,应注意寻求简捷方法 解答历年有关数列的客观题,就会发现,除了常规方法外,还可以用更简捷的方法求解.现介绍如下: ①借助特殊数列. ②灵活运用等差数列、等比数列的有关性质,可更加准确、快速地解题,这种思路在解客观题时表现得更为突出,很多数列客观题都有灵活、简捷的解法
5.在数列的学习中加强能力训练 数列问题对能力要求较高,特别是运算能力、归纳猜想能力、转化能力、逻辑推理能力更为突出.一般来说,考题中选择、填空题解法灵活多变,而解答题更是考查能力的集中体现,尤其近几年高考加强了数列推理能力的考查,应引起我们足够的重视.因此,在平时要加强对能力的培养。
6.这几年的高考通过选择题,填空题来着重对三基进行考查,涉及到的知识主要有:等差(比)数列的性质. 通过解答题着重对观察、归纳、抽象等解决问题的基本方法进行考查,其中涉及到方程、不等式、函数思想方法的应用等,综合性比较强,但难度略有下降.
四、复习建议
1. 对基础知识要落实到位,主要是等差(比)数列的定义、通项、前n项和.
2. 注意等差(比)数列性质的灵活运用.
3. 掌握一些递推问题的解法和几类典型数列前n项和的求和方法.
4. 注意渗透三种数学思想:函数与方程的思想、化归转化思想及分类讨论思想.
5. 注意数列知识在实际问题中的应用,特别是在利率,分期付款等问题中的应用.
6. 数列是高中数学的重要内容之一,也是高考考查的重点。而且往往还以解答题的形式出现,所以我们在复习时应给予重视。近几年的高考数列试题不仅考查数列的概念、等差数列和等比数列的基础知识、基本技能和基本思想方法,而且有效地考查了学生的各种能力。
五、典型例题
数列的概念与性质
【例1】
已知由正数组成的等比数列![]() ,若前
,若前![]() 项之和等于它前
项之和等于它前![]() 项中的偶数项之和的11倍,第3项与第4项之和为第2项与第4项之积的11倍,求数列
项中的偶数项之和的11倍,第3项与第4项之和为第2项与第4项之积的11倍,求数列![]() 的通项公式.
的通项公式.
解:∵q=1时![]() ,
,![]()
又![]() 显然
显然![]() ,q≠1
,q≠1
∴![]()
依题意![]() ;解之
;解之![]()
又![]() ,
,
依题意![]() ,将
,将![]() 代入得
代入得![]()
![]()
【例2】
等差数列{an }中,![]() =30,
=30,![]() =15,求使an≤0的最小自然数n。
=15,求使an≤0的最小自然数n。
解:设公差为d,则![]() 或
或![]() 或
或![]() 或
或![]()
解得:![]() Þ a33
= 30 与已知矛盾 或
Þ a33
= 30 与已知矛盾 或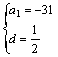 Þ a33
= - 15 与已知矛盾
Þ a33
= - 15 与已知矛盾
或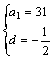 Þa33 = 15 或
Þa33 = 15 或![]() Þ a33 = - 30 与已知矛盾
Þ a33 = - 30 与已知矛盾
∴an = 31+(n - 1) (![]() ) Þ 31
) Þ 31 ![]() 0 Þ n≥63
0 Þ n≥63
∴满足条件的最小自然数为63。
【例3】
设等差数列{a![]() }的前n项和为S
}的前n项和为S![]() ,已知S4=44,S7=35
,已知S4=44,S7=35
(1)求数列{a![]() }的通项公式与前n项和公式;
}的通项公式与前n项和公式;
(2)求数列![]() 的前n项和Tn。
的前n项和Tn。
解:(1)设数列的公差为d,由已知S4=44,S7=35可得a1=17,d=-4
∴a![]() =-4n+21
(n∈N),S
=-4n+21
(n∈N),S![]() =-2n
=-2n![]() +19 (n∈N).
+19 (n∈N).
(2)由a![]() =-4n+21≥0 得n≤
=-4n+21≥0 得n≤![]() , 故当n≤5时,a
, 故当n≤5时,a![]() ≥0, 当n≥6时,
≥0, 当n≥6时,![]()
当n≤5时,T![]() =S
=S![]() =-2n
=-2n![]() +19n 当n≥6时,T
+19n 当n≥6时,T![]() =2S5-S
=2S5-S![]() =2n
=2n![]() -19n+90.
-19n+90.
【例4】
已知等差数列![]() 的第2项是8,前10项和是185,从数列
的第2项是8,前10项和是185,从数列![]() 中依次取出第2项,第4项,第8项,……,第
中依次取出第2项,第4项,第8项,……,第![]() 项,依次排列一个新数列
项,依次排列一个新数列![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() 及前n项和公式
及前n项和公式![]() 。
。
解:由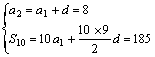 得
得 ![]()
∴![]() ∴
∴![]()
![]()
【例5】
已知数列![]() :
:![]()
①求证数列![]() 为等差数列,并求它的公差
为等差数列,并求它的公差
②设![]() ,求
,求![]() 的和。
的和。
解:①由条件,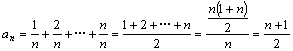
∴![]() ;∴
;∴![]()
故![]() 为等差数列,公差
为等差数列,公差![]()
②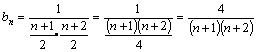
又知![]()
∴![]()
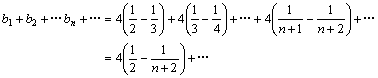
∴![]()
【例6】 已知数列1,1,2……它的各项由一个等比数列与一个首项为0的等差数列的对应项相加而得到。求该数列的前n项和Sn;
解:(1)记数列1,1,2……为{An},其中等比数列为{an},公比为q;
等差数列为{bn},公差为d,则An =an +bn (n∈N)
依题意,b1
=0,∴A1 =a1
+b1 =a1 =1 ① A![]() =a
=a![]() +b
+b![]() =a
=a![]() q+b
q+b![]() +d=1 ②
+d=1 ②
A![]() =a
=a![]() +b
+b![]() =a
=a![]() q2 +b
q2 +b![]() +2d=2 ③
+2d=2 ③
由①②③得d=-1,
q=2, ∴![]()
∴ 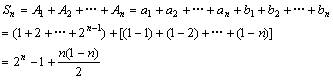
【例7】
已知数列![]() 满足an+Sn=n,(1)求a1,a2,a3,由此猜想通项an,并加以证明。
满足an+Sn=n,(1)求a1,a2,a3,由此猜想通项an,并加以证明。
解法1:由an+Sn=n,
当n=1时,a1=S1,\a1+a1=1,得a1=![]()
当n=2时,a1+a2=S2,由a2+S2=2,得a1+2a2=2,\a2=![]()
当n=3时,a1+a2+a3=S3,由a3+S3=3,得a1+a2+2a3=3\a3=![]()
猜想,![]() (1)下面用数学归纳法证明猜想成立。
(1)下面用数学归纳法证明猜想成立。
当n=1时,a1=1-![]() ,(1)式成立
,(1)式成立
假设,当n=k时,(1)式成立,即ak=1-![]() 成立,
成立,
则当n=k+1时,ak+1+Sk+1=k+1,Sk+1=Sk+ak+1
\2ak+1=k+1-Sk 又ak=k+Sk
\2ak+1=1+ak \ak+1=![]()
即当n=k+1时,猜想(1)也成立。
所以对于任意自然数n,![]() 都成立。
都成立。
解法2:由an+Sn=n得![]() ,两式相减得:
,两式相减得:![]() ,
,
即![]() ,即
,即![]() ,下略
,下略
【例8】
设数列![]() 是首项为1的等差数列,数列
是首项为1的等差数列,数列![]() 是首项为1的等比数列,又
是首项为1的等比数列,又
![]() 。(1)求数列
。(1)求数列![]() 的通项公式与前n项和公式;
的通项公式与前n项和公式;
(2)当![]() 时,试判断cn的符号(大于零或小于零),并给予严格证明。
时,试判断cn的符号(大于零或小于零),并给予严格证明。
解:(1)设数列![]() 的公比为q
的公比为q
![]()
![]()
由条件得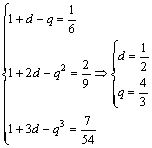
![]()
![]()
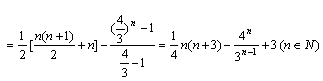
(2)![]()
证明:①当n=5,c5<0命题成立
②假设当![]()
![]()
当![]() 也成立
也成立
由①,②对一切n![]() 5,都有cn<0。
5,都有cn<0。
【例9】
![]() 是等差数列,数列
是等差数列,数列![]() 满足
满足![]() 的前n项和。(1)若
的前n项和。(1)若![]() 的公差等于首项a1,证明对于任意自然数n都有
的公差等于首项a1,证明对于任意自然数n都有![]() ;
;
(2)若![]() 中满足
中满足![]() ,试问n多大时,Sn取得最大值?证明你的结论。
,试问n多大时,Sn取得最大值?证明你的结论。
解:(1)当![]() ,∴原命题成立
,∴原命题成立
假设当![]() 成立
成立
则![]()
![]()
![]()
(2)由![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
故![]() 中
中![]() 最大
最大
【例10】
已知数列![]() 的前n项和为Sn,满足条件
的前n项和为Sn,满足条件![]() ,其中b>0且b
,其中b>0且b![]() 1。(1)求数列
1。(1)求数列![]() 的通项an;(2)若对4
的通项an;(2)若对4![]() ,试求b的取值范围。
,试求b的取值范围。
解:(1)由已知条件得![]()
当n=1时,![]()
故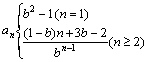
(2)由![]()
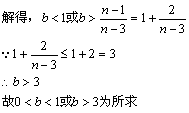
【例11】
两个数列![]() 、
、![]() 中,
中,![]() 成等差数列,且
成等差数列,且![]() 成等比数列。(1)证明
成等比数列。(1)证明![]() 是等差数列;(2)若
是等差数列;(2)若![]() 的值。
的值。
解:(1)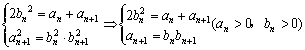
![]() 是等差数列
是等差数列
(2)又![]() ,
,
又![]()
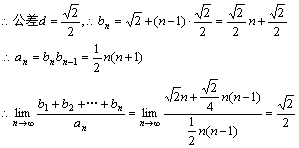
数列的概念与性质练习
一、选择题
1.设![]() ( D )
( D )
A.![]()
B.![]()
C.![]()
D.![]()
2.等比数列![]() 中,
中,![]() ,那么
,那么
![]() 的值为( C )
的值为( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.11.等比数列 {a![]() } 中,a
} 中,a![]() =7,前三项之和 S
=7,前三项之和 S![]() =21,则公比q的值是( C )
=21,则公比q的值是( C )
(A) 1 (B) -![]() (C) 1或 -
(C) 1或 -![]() (D) -1或
(D) -1或![]()
4.首项为1,公差不为零的等差数列中的![]() 是一个等比数列的前3项,则这一等
是一个等比数列的前3项,则这一等
比数列的第四项为( B )
A.8 B.-8 C.-6 D.不确定
5.已知数列![]() 的前n项和
的前n项和![]() ,那么这个数列中的奇数项依照原来的顺序构
,那么这个数列中的奇数项依照原来的顺序构
成的数列的通项公式是( B )
A.![]() B.
B.![]()
C.![]() D.
D. ![]()
6.数列{an}的前n项和Sn=3n-2n2 (n∈N),当n>2时,就有( D )
A.Sn>na1>nan B.Sn< nan<na1 C.na1<Sn<nan D.nan<Sn<na1
7.有下列命题:
①x=![]() 是a, x, b成等比数列的充分但不必要条件
是a, x, b成等比数列的充分但不必要条件
②某数列既是等差数列又是等比数列,则这个数列一定是常数列
③已知Sn表示数列{an}的前n项和,且S![]() ,那么{an}一定是等比数列
,那么{an}一定是等比数列
④设![]() ,则这三个数a, b, c成等差数列
,则这三个数a, b, c成等差数列
其中正确的命题序号是:( D )
A.②④ B.①②③ C.①③ D.①②④
8.若两个等差数列![]() 的前n项和
的前n项和![]() (nÎN),则
(nÎN),则![]() 的值等于( C )
的值等于( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.在等差数列![]() 中,3(a3+a5)+2(a7+a10+a13)=24,则此数列前13项之和为( A )
中,3(a3+a5)+2(a7+a10+a13)=24,则此数列前13项之和为( A )
A.26 B.13 C.52 D.156
10.等差数列![]() ,
,![]() =-5,它的前11项的算术平均值为5。若从中抽去一项,余下10
=-5,它的前11项的算术平均值为5。若从中抽去一项,余下10
项的算术平均值为4,则抽去的是( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.已知数列![]() 的前n项和的公式为
的前n项和的公式为![]() ,则通项公式为 。
,则通项公式为 。![]()
2.数列{a![]() }的通项公式为
}的通项公式为 ![]() 前n项和为
S
前n项和为
S![]() ,若
,若![]()
(a为实常数),则a的值等于 。3
三、解答题
1.![]()
![]()
(1)![]() (2)
(2)![]()
(3)![]()
解:(1)![]()
![]()
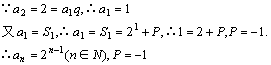
(2)
![]()
![]()
![]()
②-①得
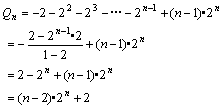
![]()
(3)当n=2k(k∈N)时,
![]()
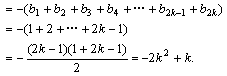
当n=2k-1 (k∈N)时,
![]()
![]()
![]()
2.数列![]() 的前n项和为Sn, 已知
的前n项和为Sn, 已知![]() 是各项为正数的等比数列。试比较
是各项为正数的等比数列。试比较![]() 的大小,证明你的结论。
的大小,证明你的结论。
解:依题意, 可设![]()
则![]()
从而有![]()
(Ⅰ)当q = 1时, a2 = a3 = … = 0
∴![]()
(Ⅱ)当q > 0且![]() 时,
时,
(1)当n =
1时, ![]()
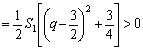
∴![]()
(2)当![]()
![]()
(i)若q
> 1时, 则![]()
(ii)若0 < q < 1时, 则![]()
3.已知数列![]()
(1)分别求出![]() 。
。
(2)当n³9且n是自然数时,试比较![]() 与2的大小,并说明理由。
与2的大小,并说明理由。
解:(1)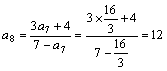 ;
;![]()
(2)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 时命题成立
时命题成立
![]()
4.已知![]() ,
,![]()
⑴比较![]() 与
与![]() 的大小。
的大小。
⑵试确定实数![]() 的取值范围,使得对于一切大于1的自然数
的取值范围,使得对于一切大于1的自然数![]() ,不等式
,不等式![]() 恒成立。
恒成立。
解:(1)∵f(n+1)-f(n)=S2n+3-Sn+2-(S2n+1-Sn+1)=…=![]()
>![]() =0,
=0,
∴f(n+1)>f(n)。
(2)∵f(n+1)>f(n),∴当n>1时,f(n)的最小值为f(2)=S5-S3=![]()
∴必需且只须![]() <
<![]() ……………①,
……………①,
由![]() 得m>1且m≠2
得m>1且m≠2
令t=![]() 则不等式①等价于
则不等式①等价于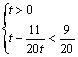 ,解得:0<t<1
,解得:0<t<1
即0<![]() <1,即-1<logm(m-1)<0或0<logm(m-1)<1,
<1,即-1<logm(m-1)<0或0<logm(m-1)<1,
解之得:![]() 。
。
5.某人年初向建设银行贷款10万元用于买房。
(1)如果他向建设银行贷款, 年利率为5%, 且这笔借款分10次等额归还(不计复利), 每年一次, 并从借后次年年初开始归还, 问每年应还多少元(精确到1元)?
(2)如果他向工商银行贷款, 年利率为4%, 要按复利计算(即本年的利息计入次年的本金生息), 仍分10次等额归还, 每年一次, 每年应还多少元(精确到1元)?
解:(1) 若向建设银行贷款, 设每年还款x元, 则
105×(1 + 10×5%) = x(1 + 9×5%) + x(1 + 8×5%) + x(1 + 7×5%) + … + x,
105×1.5 = 10x + 45×0.05x,
解得![]() (元)
(元)
(2)若向工商银行贷款, 设每年还款y元, 则
105×(1 + 4%)10 = y(1 + 4%)9 + y(1 + 4%)8 + y(1 + 4%)7 + … + y
![]()
其中1.0410 = (1 + 0.04)10 = 1 + 10×0.04 + 45×0.042 + 120×0.043 + 210×0.044
+ …![]() 1.4802
1.4802
![]() (元)
(元)
答: 若向建设银行贷款, 每年需还12245元; 若向工商银行贷款, 每年需还12330元。
数列的综合应用(1)
【例1】
已知无穷数列{an},Sn是其前n项和,对不小于2的正整数n,满足关系![]() 。(1)求a1,a2,a3;(2)证明{an}是等比数列;
。(1)求a1,a2,a3;(2)证明{an}是等比数列;
(3)设![]() 计算
计算![]()
解:(1)S2=![]()
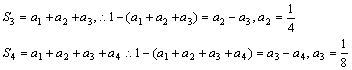
(2)猜想 a![]()
(1) 当n=1时,命题成立
(2)
假设n=k(k≥1)时命题成立,即![]()
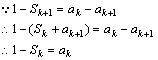 (*)
(*)
同理有 1-Sk+1=ak+1 (**)
由(*)式和假设![]()
由(**)式,得,1=(Sk+ak+1)
故 ak+1=![]()
∴当n=k+1时,命题也成立。
由(1),(2)n∈N,a![]()
此时 ![]()
(2)另证:对 n≥2, 1-Sn=an-1-an
1- Sn+1=an-an+1
两式相减,有
![]()
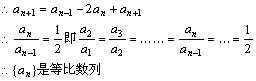
(3)![]()
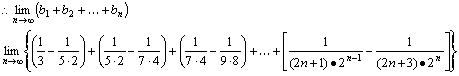
=![]()
【例2】
已知![]() ,数列
,数列 ![]() 满足
满足![]()
![]()
(1)写出数列![]() 的前五项,试归纳出
的前五项,试归纳出![]() 的表达式,并用数学归纳法证明。
的表达式,并用数学归纳法证明。
(2)求![]() 。(3)若
。(3)若![]() 求数列
求数列![]() 的前n项的和Sn。
的前n项的和Sn。
解:(1)由![]() 得数列前五项
得数列前五项
![]()
![]()
(ii)假设![]() 时等式①成立,即
时等式①成立,即![]()
当![]() 时
时![]()
即等式①对![]() 也成立
也成立
由(i)(ii)可知等式①对![]() 都成立
都成立
(2)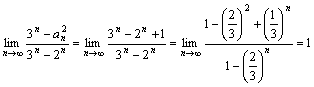
(3)![]()
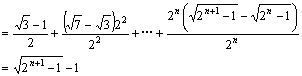
【例3】 已知a>0,a≠1,数列{an}是首项为a,公比也为a的等比数列,令bn=anlgan
(n∈N)。(1)求数列{bn}的前n项和Sn;
(2)当数列{bn}中的每一项总小于它后面的项时,求a的取值范围.
解:(1)由题意知an=an,bn=nanlga.
∴Sn=(1 • a+2 • a2+3 • a3+……+n • an)lga.
a Sn=(1 • a2+2 • a3+3 • a4+……+n • an+1)lga.
以上两式相减得
(1–a)Sn=(a+a2+a3+……+an–n • an+1)lga ![]() .
.
∵a≠1,∴![]() .
.
(2)由bk+1–bk=(k+1)ak+1lga–kaklga=aklga[k(a–1)+a].
由题意知bk+1–bk>0,而ak>0,
∴lga[k(a–1)+a]>0. ①
(1)若a>1,则lga>0,k(a–1)+a>0,故a>1时,不等式①成立;
(2)若0<a<1,则lga<0,
不等式①成立![]()
![]() 恒成立
恒成立
![]() .
.
综合(1)、(2)得a的取值范围为![]()
【例4】
已知数列{an}的前n项和为Sn,又有数列{bn},它们满足关系![]() ,对
,对![]() 有
有![]() 。
。
(1)求证{bn}是等比数列,并写出它的通项公式
(2)求![]()
解:⑴证法一:当
n=1时,![]() 。
。
![]()
同理,![]()
(2)-(1),![]()
即![]()
由![]()
于是![]()
由(3),(4)知![]() 的等比数列,
的等比数列,![]()
证法二:同上算得![]() ,……猜想
,……猜想![]() 且数学归纳法证明,
且数学归纳法证明,
(1) 当![]() ,命题成立
,命题成立
(2)假设![]() 时命题成立,即
时命题成立,即![]() 成立。
成立。
![]()
∴ ![]()
又![]()
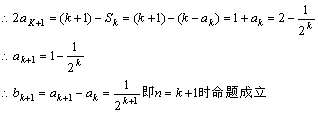
由(1)(2)知对 ![]() 猜想
猜想![]() 成立
成立
![]() 的等比数列,
的等比数列,![]()
⑵![]()
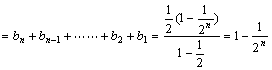
∴![]()
解法2:由![]()
![]()
![]() ,∴{bn}是等比数列;且
,∴{bn}是等比数列;且![]()
【例5】
已知![]() 是首项为1,公差为d的等差数列,其前n项和为
是首项为1,公差为d的等差数列,其前n项和为![]() ,
,![]() 是首项为1,公比为q(q<1)的等比数列,其前n项和为
是首项为1,公比为q(q<1)的等比数列,其前n项和为![]() ,设
,设![]() ,若
,若![]() ,求d和q。
,求d和q。
解:![]() ;
;![]()
又![]() ;
;
![]()
![]()
![]()
![]()
![]() =1
=1
![]()
![]()
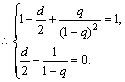
![]()
又![]()
【例6】
已知等比数列![]() 中a1 =
1,公比为x (x > 0),其前n项和为S。
中a1 =
1,公比为x (x > 0),其前n项和为S。
(1)写出数列![]() 的通项公式及前n项和Sn的公式;(2)设
的通项公式及前n项和Sn的公式;(2)设![]() ,写出bn关于x和n的表达式;(3)判断数列{bn}的增减性;(4)求
,写出bn关于x和n的表达式;(3)判断数列{bn}的增减性;(4)求![]() 。
。
解:(1)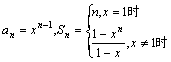
(2)![]()
![]()
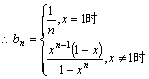
(3)当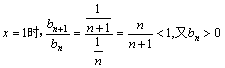 ;∴
;∴![]()
当n![]() 1时,
1时,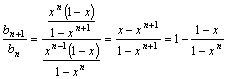

综上知![]() 为递减数列。
为递减数列。
(4)当![]()
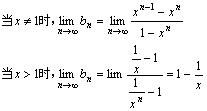
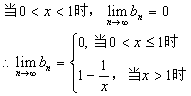
数列的综合应用(1)
一、选择题
1.等差数列![]() 的通项公式为
的通项公式为![]() 的前n项和S
的前n项和S![]() 等于( A )
等于( A )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
2.一个等比数列的前n项和![]() ,则该数列各项和为( B )
,则该数列各项和为( B )
A.![]() B.1 C.-
B.1 C.-![]() D.任意实数
D.任意实数
3.已知数列{an}满足an+1=an–an–1(n≥2),a1=a,a2=b,记Sn=a1+a2+a3+…+an,则下列结
论正确的是( A ).
(A)a100=–a,S100=2b–a (B)a100=–b,S100=2b–a
(C)a100=–b,S100=b–a (D)a100=–a,S100=b–a
4.设首项为3,公比为2的等比数列{a![]() }的前n项和为S
}的前n项和为S![]() ,首项为2,公比为3的等比
,首项为2,公比为3的等比
数列{a'![]() }的前n项和为S'
}的前n项和为S'![]() ,则
,则![]() 的值等于( C )
的值等于( C )
(A) ![]() (B)
(B)
![]() (C)
(C)
![]() (D) 2
(D) 2
5.在等比数列![]() 中,首项a1
< 0,则
中,首项a1
< 0,则![]() 是递增数列的充要条件是公比q满足
是递增数列的充要条件是公比q满足
( C )
A.q > 1 B.q < 1 C.0 < q < 1 D.q < 0
6.设首项为3,公比为2的等比数列 {a![]() } 的前n项和为S
} 的前n项和为S![]() ,首项为2、公比为3的等
,首项为2、公比为3的等
比数列{a![]() } 的前n项和为 S
} 的前n项和为 S![]() ’,则
’,则 ![]() 的值等于:( C )
的值等于:( C )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D) 2
(D) 2
7.已知数列![]() 中,
中,![]() ,则这个数列前n项和的极限是(A)
,则这个数列前n项和的极限是(A)
(A)2 (B)![]() (C)3 (D)
(C)3 (D)![]()
8.等差数列![]() 的通项
的通项![]() ,则由
,则由![]() 所确定的数列
所确定的数列![]() 的前n项和是( C )
的前n项和是( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知等比数列{an}中,公比q![]() R,且
R,且![]() ,
,![]() ,记
,记
![]() 则
则![]() Sn等于( D )
Sn等于( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:由已知可得![]()
所以得:![]()
所以![]()
10.已知数列![]() 此数列所有项的和等于( C )
此数列所有项的和等于( C )
A.0.25 B.0.5 C.0.3 D.0.375
二、填空题
1.设等差数列![]() 共有3n项,它的前2n项之和是100,后2n项之和是200,则该等差数列的中间n项之和等于
. 75
共有3n项,它的前2n项之和是100,后2n项之和是200,则该等差数列的中间n项之和等于
. 75
2.在数列![]() 该数列所有项的和为
该数列所有项的和为![]() ,则
,则![]() 的值等于
的值等于 ![]()
3.某工厂原来年总产值为a,以后连续两年平均以10%递增,若连续两年中第二年产值为b,则a占b的百分数是
。![]()
4.数列![]() 中,
中,![]() 。
。![]()
5.已知![]() 、
、![]() 都是公差不为零的等差数列,且
都是公差不为零的等差数列,且![]()
则![]() 的值为 。
的值为 。![]()
6.已知数列![]() 是等比数列,若
是等比数列,若![]()
且![]() . 16
. 16
三、解答题
1.数列![]() 中,前n项和
中,前n项和![]() 其中a,b是常数,且a>0,a+b>1,n∈N.
其中a,b是常数,且a>0,a+b>1,n∈N.
(1)求![]() 的通项公式
的通项公式![]() ,并证明
,并证明![]() ;
;
(2)令![]() ,试判断数列
,试判断数列![]() 中任意相邻两项的大小.
中任意相邻两项的大小.
解:(1)![]()
![]()
![]()
当n=1时也能满足上式,∴![]()
![]()
∴![]()
(2)由(1)及对数的性质可得数列![]() 中各项皆为正值
中各项皆为正值
![]()
![]()
![]()
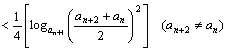
![]()
又∵![]() ,∴
,∴![]() .
.
∴![]()
2.已知数列![]() ,前n项和为
,前n项和为![]() ,对于任意
,对于任意![]() 总成等差数列。(1)求
总成等差数列。(1)求![]() 的值;(2)求通项
的值;(2)求通项![]() (3)计算
(3)计算![]() .
.
解:(1)∵当n≥2时,![]() 成等差数列
成等差数列
∴![]() ;∴
;∴![]()
∴![]() ∵
∵![]() ,∴
,∴![]()
类似地![]() ∴
∴![]()
![]() ∴
∴ ![]()
(2)∵当n≥2时,![]() ,即
,即![]()
∴![]()
②–①得![]() ∴
∴![]() 为常数
为常数
∴![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…成等比数列.;其中
,…成等比数列.;其中![]()
故![]()
∴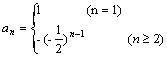
(3)∵![]() =
=![]()
∴![]() =
=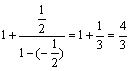
数列的综合应用(2)
【例1】
已知函数![]() 具有下列性质:
具有下列性质:
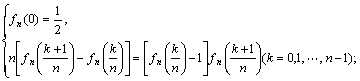
(1)当n一定,记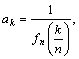 求
求![]() 的表达式
的表达式![]()
(2)对![]()
解:(1)![]()
![]()
![]()
即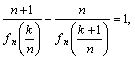 又
又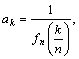
![]()
![]() ,即
,即![]() ,由n为定值,
,由n为定值,
则数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,
为公比的等比数列,
![]() ,
,
由于![]()
(2)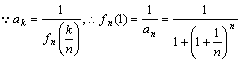 ,
,
欲证![]() ,
,
只需证明![]() ,
,
只需证明![]()
![]()
![]()
![]()
![]()
![]()
![]()
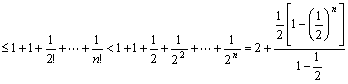
![]()
【例2】
已知函数f(x)=![]()
(1)求f(x)的反函数f-1 (x)的表达式;
(2)数列![]() 中,a1 =1;an =f-1 (an-1)(nÎN,n≥2),如果bn =
中,a1 =1;an =f-1 (an-1)(nÎN,n≥2),如果bn =![]() (nÎN),求数列
(nÎN),求数列![]() 的通项公式及前n项和Sn;
的通项公式及前n项和Sn;
(3)如果g(n)=2Sn-17n,求函数g(x) (xÎR)在区间[t,t+2] (tÎR)上的最小值h(t)的表达式。
解:(1)![]()
![]() ∴f-1 (x)=
∴f-1 (x)=
![]()
(2)![]()
∴![]() ∴
∴![]()
![]() 是以1为首项,公差为1的等差数列
是以1为首项,公差为1的等差数列 ![]()
![]()
(3)g(n)=2Sn-17n=n2-16n ![]() xÎR
xÎR
∴g(x)函数图像是以顶点M(8,-64)且开口向上的抛物线
(i)当t>8时,g(x)在[t,t+2]上是增函数 ∴h(t)=g(t)=t2-16t
(ii)当t+2<8时,g(x)在[t,t+2]是减函数 ∴h(t)=g(t+2)=t2-12t-28
(iii)当6≤t≤8时 h(t)=g(8)=-64
∴
【例3】
在数列{an}中,已知![]()
(1)求证:![]() ;(2)求证:
;(2)求证:![]() ;
;
(3)若存在![]() ,使得
,使得![]() ,求证:
,求证: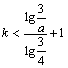 。
。
解:(1)证明:
当![]() ,命题成立。
,命题成立。
假设![]() 时,命题成立,即
时,命题成立,即![]()
则![]()
由归纳假设![]() ,则
,则![]() ,由平均值定理得
,由平均值定理得
![]()
所以![]() 时
时![]() 也成立
也成立
因此,对任意自然数n,都有![]()
(2)证明:![]() ;由(1)
;由(1)![]() ,
,![]()
又![]()
(3)证明:由![]() 及
及![]() 得
得![]()
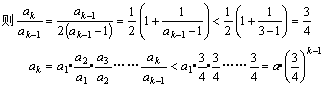
![]()
由此得![]() ;于是
;于是![]()
又![]() ,解得
,解得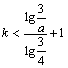
【例4】
已知数列{an}满足a1=2,对于任意的n∈N,都有an>0,且(n+1)a![]() +anan+1-na
+anan+1-na![]() =0,又知数列{bn}:b1=2n-1+1。(1)求数列{an}的通项an以及它的前n项和Sn;(2)求数列{bn}的前n项和Tn;(3)猜想Sn和Tn的大小关系,并说明理由.
=0,又知数列{bn}:b1=2n-1+1。(1)求数列{an}的通项an以及它的前n项和Sn;(2)求数列{bn}的前n项和Tn;(3)猜想Sn和Tn的大小关系,并说明理由.
解:⑴∵![]()
∴ ![]() 。
。
∴ 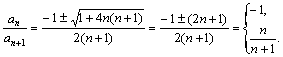
∴![]() ,∴
,∴![]() 。即
。即![]() 。
。
∴![]()
![]() 。∴
。∴![]() ,
,
又![]() ,∴
,∴![]() 。
。
∴![]()
![]() 。
。
⑵∴![]() ,
,
∴![]()
![]()
![]() 。
。
⑶![]()
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() ;
;
当![]() 时,
时,![]() ,∴
,∴![]() 。
。
猜想:当![]() 时,
时,![]() 。
。
即![]() 。亦即
。亦即![]() 。
。
下面用数学归纳法证明:
![]() 当
当![]() 时,前面已验证成立;
时,前面已验证成立;
![]() 假设
假设![]() 时,
时,![]() 成立,那么当
成立,那么当![]() 时,
时,
![]()
![]()
![]()
![]() 。
。
∴当![]() 时,
时,![]() 也成立。
也成立。
由以上![]() 、
、![]() 可知,当
可知,当![]() 时,有
时,有![]() ;当
;当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 。
。
【例5】
已知等差数列{![]() }中,公差为d>0,等比数列{
}中,公差为d>0,等比数列{![]() }中,
}中,![]() 公比q>0且
公比q>0且![]() 若
若![]() ,求a的取值范围.
,求a的取值范围.
解:由已知不等式,得![]()
![]() ∵
∵![]() ,∴
,∴![]()
①当![]() 时,
时,![]() ,∵
,∵![]() ,∴
,∴![]()
∵若![]() ,则
,则![]() ,∴
,∴![]()
若![]() ,则
,则![]() ,∴
,∴![]()
②当![]() 时,
时,![]()
∵![]() ,∴
,∴![]()
若![]() ,则
,则![]() ,∴
,∴![]()
若![]() 时,则
时,则![]() ,∴
,∴![]()
综上:若![]() 时,
时, ![]() 或
或![]()
![]() 时,
时,![]() 或
或![]()
数列的综合应用(2)练习
一、选择题
1.设Sn =![]() ,则
,则![]() 等于( A )
等于( A )
A.![]() B.
B.![]() C.0 D.
C.0 D.![]()
2.已知数列![]() 中,
中,![]() ,那么
,那么![]() 等于( B )
等于( B )
A、-495 B、765 C、1080 D、3105
3.在等差数列![]() 中,
中,![]() ( A )
( A )
A、0 B、m C、n D、不确定
4.一个等差数列的首项为4,它的第一项、第七项、与第十项成等比数列,这个数列的通项公式是( C )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5.设![]() 等于( C )
等于( C )
A、![]() B、
B、![]() C、
C、![]() D、1
D、1
6.数列1,b,c,8中,前三项1,b,c成等差数列,后三项b,c,8成等比数列,则必有( B )
A、c>0 B、b>0 C、c<0 D、b<0
7.设等差数列的前4项之和为26,其末4项之和为110,又这个数列的所有的项之和为
187,则这个数列共有多少项( A )
A、11项 B、22项 C、8项 D、项数不能确定
8.设数列![]() 满足
满足![]() 且
且![]() 等于( D )
等于( D )
A、100a B、100a2 C、101a100 D、100a100
二、填空题
1.若等差数列![]() 的前几项和为Sn,且
的前几项和为Sn,且![]() 。100
。100
2.已知数列![]() ,
,![]() 它的前n项和记为Sn,若
它的前n项和记为Sn,若![]() 是一个首项为a
是一个首项为a
公比为q(q>0)的等比数列,且![]() .
.
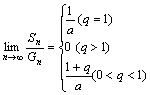
3.在等比数列![]() 中,记:
中,记:![]() ,若
,若![]() 则公比q= 3
则公比q= 3
4.数列![]() 的前n项和为
的前n项和为![]() 的值为 。1
的值为 。1
5.数列![]() 的通项公式
的通项公式![]() 前n项和为
前n项和为![]() (a为实常数),则a的值等于
。2
(a为实常数),则a的值等于
。2
6.已知等比数列![]() 的各项都是正数,
的各项都是正数,![]() ,且前n项中最大的一项为54,
,且前n项中最大的一项为54,
则n= 。4
三、解答题
1、若![]() 分别表示数列
分别表示数列![]() 的前n项的和,对任意正整数n,
的前n项的和,对任意正整数n,![]()
![]() 。(1)求数列
。(1)求数列![]() 的通项公式;
的通项公式;
(2)在平面直角坐标系内,直线![]() 的斜率为
的斜率为![]() ,且与曲线
,且与曲线![]() 有且仅有一个交点,与y
有且仅有一个交点,与y
轴交于点Dn,记![]() ;
;
(3)若![]() .
.
解:(1)解法(一)由已知![]()
当![]()
由于![]()
由于b1适合上式,![]()
解法(二)由于![]() 为等差数列,
为等差数列,![]()
![]()
![]()
当n=1时,![]() ,
,
当![]()
由于b1适合上式,![]()
(2)设![]() 的方程为
的方程为![]()
![]()
∵直线![]() 与曲线只有一个交点,∴
与曲线只有一个交点,∴![]()
∴![]() 则
则![]()
从而![]()
![]()
![]()
![]()
(3)![]()
![]()
=![]()
![]()
2.![]() 都是各项为正的数列,对任意的自然数
都是各项为正的数列,对任意的自然数![]() ,都有
,都有![]() 成等差数列
成等差数列![]() ,
,![]() 成等比数列。
成等比数列。
(1)试问![]() 是否是等差数列?为什么?
是否是等差数列?为什么?
(2)求证:对任意的自然数![]() 成立;
成立;
(3)如果![]() ,求
,求![]() 。
。
解:依题意![]() ……①
……①
![]() ……②
……②
(1)∵![]() ,∴由②式得
,∴由②式得![]()
从而![]() 时,
时,![]()
代入①![]() ,∴
,∴![]()
∴![]() 是等差数列。
是等差数列。
(2)因为![]() 是等差数列∴
是等差数列∴![]()
∴![]()
(3)由![]() 及①②两式易得
及①②两式易得![]()
∴![]() 中公差
中公差![]()
∴![]()
∴![]() ………………③
………………③
又![]() 也适合③、∴
也适合③、∴![]()
∴![]()
∴![]()
∴![]()