08高考数学直线与圆的方程
一、重点知识结构
本章以直线和圆为载体,揭示了解析几何的基本概念和方法。
直线的倾斜角、斜率的概念及公式、直线方程的五种形式是本章的重点之一,而点斜式又是其它形式的基础;
两条直线平行和垂直的充要条件、直线l1到l2的角以及两直线的夹角、点到直线的距离公式也是重点内容;
用不等式(组)表示平面区域和线性规划作为新增内容,需要引起一定的注意;
曲线与方程的关系体现了坐标法的基本思想,是解决解析几何两个基本问题的依据;
圆的方程、直线(圆)与圆的位置关系、圆的切线问题和弦长问题等,因其易与平面几何知识结合,题目解法灵活,因而是一个不可忽视的要点。
二、高考要求
1、掌握两条直线平行和垂直的条件,掌握两条直线所成的角和点到直线的距离公式,能够根据直线的方程判断两条直线的位置关系;
3、会用二元一次不等式表示平面区域;
4、了解简单的线性规划问题,了解线性规划的意义,并会简单的应用;
5、了解解析几何的基本思想,了解用坐标法研究几何问题的方法;
6、掌握圆的标准方程和一般方程,了解参数方程的概念,理解圆的参数方程的概念。
三、热点分析
在近几年的高考试题中,两点间的距离公式,中点坐标公式,直线方程的点斜式、斜率公式及两条直线的位置关系是考查的热点。但由于知识的相互渗透,综合考查直线与圆锥曲线的关系一直是高考命题的大热门,应当引起特别注意,本章的线性规划内容是新教材中增加的新内容,在高考中极有可能涉及,但难度不会大。
四、复习建议
本章的复习首先要注重基础,对基本知识、基本题型要掌握好;求直线的方程主要用待定系数法,复习时应注意直线方程各种形式的适用条件;研究两条直线的位置关系时,应特别注意斜率存在和不存在的两种情形;曲线与方程的关系体现了坐标法的基本思想,随着高考对知识形成过程的考查逐步加强,对坐标法的要求也进一步加强,因此必须透彻理解。既要掌握求曲线方程的常用方法和基本步骤,又能根据方程讨论曲线的性质;圆的方程、直线与圆的位置关系,圆的切线问题与弦长问题都是高考中的热点问题;求圆的方程或找圆心坐标和半径的常用方法是待定系数法及配方法,应熟练掌握,还应注意恰当运用平面几何知识以简化计算。
直线
【例题】
【例1】
已知点B(1,4),C(16,2),点A在直线x-3y+3 = 0上,并且使![]() ABC的面积等于21,求点A的坐标。
ABC的面积等于21,求点A的坐标。
解:直线BC方程为2x+5y-22 = 0,BC = ![]() ,设点A坐标(3y-3,y),则可求A到BC的距离为
,设点A坐标(3y-3,y),则可求A到BC的距离为![]() ,∵
,∵![]() ABC面积为21,∴
ABC面积为21,∴![]() ,
,
∴![]() ,故点A坐标为(
,故点A坐标为(![]() )或(
)或(![]() ).
).
【例2】 已知直线l的方程为3x+4y-12=0, 求直线l′的方程, 使得:
(1) l′与l平行, 且过点(-1,3) ;
(2) l′与l垂直, 且l′与两轴围成的三角形面积为4.
解: (1) 由条件, 可设l′的方程为 3x+4y+m=0, 以x=-1, y=3代入,
得 -3+12+m=0, 即得m=-9, ∴直线l′的方程为 3x+4y-9=0;
(2) 由条件, 可设l′的方程为4x-3y+n=0, 令y=0, 得![]() , 令x=0, 得
, 令x=0, 得![]() , 于是由三角形面积
, 于是由三角形面积![]() , 得n2=96, ∴
, 得n2=96, ∴![]()
∴直线l′的方程是![]() 或
或![]()
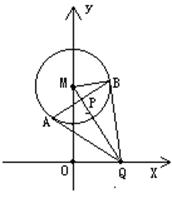
【例3】 过原点的两条直线把直线2x+3y-12 = 0在坐标轴间的线段分成三等分,求这二直线的夹角。
解:设直线2x+3y-12 = 0与两坐标轴交于A,B两点,
则A(0,4),B(6,0),设分点C,D,设![]() 为所求角。
为所求角。
∵![]() ,∴
,∴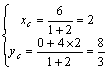 ,∴C(2,
,∴C(2,![]() ).
).
又![]() ,∴
,∴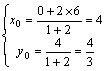 ,∴D(4,
,∴D(4,![]() ),∴
),∴![]() .
.
∴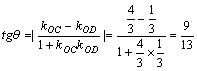 ,∴
,∴![]() .
.
【例4】
圆x2+y2+x-6y+c = 0与直线x+2y-3 = 0相交于P,Q两点,求c为何值时,OP![]() OQ(O为原点).
OQ(O为原点).
解:解方程组消x得5y2-20y+12+c = 0,![]() ,
,
消y得5x2+10x+4c-27 = 0,![]() ,
,
∵OP![]() OQ,∴
OQ,∴![]() ,∴
,∴![]() ,解得c = 3.
,解得c = 3.
【例5】 已知直线y =-2x+b与圆x2+y2-4x+2y-15 = 0相切,求b的值和切点的坐标.
解:把y =-2x+b代入x2+y2-4x+2y-15 = 0,
整理得5x2-4(b+2)x+b2+2b-15 = 0,令![]() = 0得b =-7或b =13,]
= 0得b =-7或b =13,]
∵方程有等根,![]() ,得x =-2或x = 6,
,得x =-2或x = 6,
代入y = -2x-7与y = -2x+13得y =-3或y = 1,
∴所求切点坐标为(-2,-3)或(6,1).
【例6】 已知a<1,b<1,c<1,求证:abc+2>a+b+c.
证明:设线段的方程为y=f(x)=(bc-1)x+2-b-c,其中b<1,c<1,x<1,且-1<b<1.
∵f(-1)=1-bc+2-b-c=(1-bc)+(1-b)+(1-c)>0
f(1)=bc-1+2-b-c=(1-b)(1-c)>0
∴线段y=(bc-1)x+2-b-c(-1<x<1)在x轴上方,这就是说,当a<1,b<1,c<1时,恒有abc+2>a+b+c.
【例7】 某校一年级为配合素质教育,利用一间教室作为学生绘画成果展览室,为节约经费,他们利用课桌作为展台,将装画的镜框放置桌上,斜靠展出,已知镜框对桌面的倾斜角为α(90°≤α<180°)镜框中,画的上、下边缘与镜框下边缘分别相距a m,b m,(a>b).问学生距离镜框下缘多远看画的效果最佳?
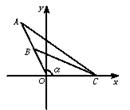 解:建立如图所示的直角坐标系,AO为镜框边,AB为画的宽度,O为下边缘上的一点,在x轴的正半轴上找一点C(x,0)(x>0),欲使看画的效果最佳,应使∠ACB取得最大值.
解:建立如图所示的直角坐标系,AO为镜框边,AB为画的宽度,O为下边缘上的一点,在x轴的正半轴上找一点C(x,0)(x>0),欲使看画的效果最佳,应使∠ACB取得最大值.
由三角函数的定义知:A、B两点坐标分别为(acosα,asinα)、
(bcosα,bsinα),于是直线AC、BC的斜率分别为:
kAC=tanxCA=![]() ,
,
![]()
于是tanACB=![]()
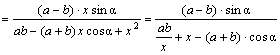
由于∠ACB为锐角,且x>0,则tanACB≤![]() ,当且仅当
,当且仅当![]() =x,即x=
=x,即x=![]() 时,等号成立,此时∠ACB取最大值,对应的点为C(
时,等号成立,此时∠ACB取最大值,对应的点为C(![]() ,0),因此,学生距离镜框下缘
,0),因此,学生距离镜框下缘![]() cm处时,视角最大,即看画效果最佳.
cm处时,视角最大,即看画效果最佳.
【例8】 预算用2000元购买单件为50元的桌子和20元的椅子,希望使桌椅的总数尽可能的多,但椅子不少于桌子数,且不多于桌子数的1.5倍,问桌、椅各买多少才行?
解:设桌椅分别买x,y张,把所给的条件表示成不等式组,即约束条件
为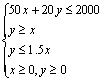 由
由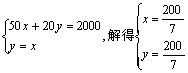
∴A点的坐标为(![]() ,
,![]() )
)
由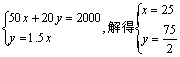
∴B点的坐标为(25,![]() )
)
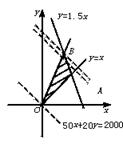 所以满足约束条件的可行域是以A(
所以满足约束条件的可行域是以A(![]() ,
,![]() ),B(25,
),B(25,![]() ),O(0,0)为顶点的三角形区域(如右图)
),O(0,0)为顶点的三角形区域(如右图)
由图形直观可知,目标函数z=x+y在可行域内的最优解为(25,![]() ),但注意到x∈N,y∈N*,故取y=37.
),但注意到x∈N,y∈N*,故取y=37.
故有买桌子25张,椅子37张是最好选择.
【例9】 已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
| 甲 | 乙 | 丙 | |
| 维生素A(单位/千克) | 600 | 700 | 400 |
| 维生素B(单位/千克) | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
(Ⅰ)用x,y表示混合食物成本c元;
(Ⅱ)确定x,y,z的值,使成本最低.
解:(Ⅰ)由题,![]() ,又
,又![]() ,所以,
,所以,![]() .
.
(Ⅱ)由![]() 得,
得,![]() ,
,
所以,![]()
所以,![]()
当且仅当![]() 时等号成立.
时等号成立.
所以,当x=50千克,y=20千克,z=30千克时,混合物成本最低,为850元.
点评:本题为线性规划问题,用解析几何的观点看,问题的解实际上是由四条直线所围成的区域 上使得
上使得![]() 最大的点.不难发现,应在点M(50,
最大的点.不难发现,应在点M(50, 20)处取得.
20)处取得.
【直线练习1】
一、选择题
1.设M=![]() ,则M与N的大小关系为( )
,则M与N的大小关系为( )
A.M>N B.M=N C.M<N D.无法判断
2.三边均为整数且最大边的长为11的三角形的个数为( )
A.15 B.30 C.36 D.以上都不对
二、填空题
3.直线2x-y-4=0上有一点P,它与两定点A(4,-1),B(3,4)的距离之差最大,则P点坐标是_________.
4.自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,则光线l所在直线方程为_________.
5.函数f(θ)=![]() 的最大值为_________,最小值为_________.
的最大值为_________,最小值为_________.
6.设不等式2x-1>m(x2-1)对一切满足m≤2的值均成立,则x的范围为_________.
三、解答题
7.已知过原点O的一条直线与函数y=log8x的图象交于A、B两点,分别过点A、B作y轴的平行线与函数y=log2x的图象交于C、D两点.
(1)证明:点C、D和原点O在同一直线上.
(2)当BC平行于x轴时,求点A的坐标.
8.设数列{an}的前n项和Sn=na+n(n-1)b,(n=1,2,…),a、b是常数且b≠0.
(1)证明:{an}是等差数列.
(2)证明:以(an,![]() -1)为坐标的点Pn(n=1,2,…)都落在同一条直线上,并写出此直线的方程.
-1)为坐标的点Pn(n=1,2,…)都落在同一条直线上,并写出此直线的方程.
(3)设a=1,b=![]() ,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1、P2、P3都落在圆C外时,r的取值范围.
,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1、P2、P3都落在圆C外时,r的取值范围.
参考答案
一、1.解析:将问题转化为比较A(-1,-1)与B(102001,102000)及C(102002,102001)连线的斜率大小,因为B、C两点的直线方程为y=![]() x,点A在直线的下方,∴kAB>kAC,即M>N.
x,点A在直线的下方,∴kAB>kAC,即M>N.
答案:A
2.解析:设三角形的另外两边长为x,y,则
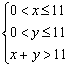
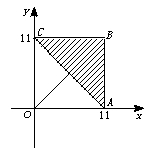 点(x,y)应在如右图所示区域内
点(x,y)应在如右图所示区域内
当x=1时,y=11;当x=2时,y=10,11;
当x=3时,y=9,10,11;当x=4时,y=8,9,10,11;
当x=5时,y=7,8,9,10,11.
以上共有15个,x,y对调又有15个,再加上(6,6),(7,7),(8,8),(9,9),(10,10)、(11,11)六组,所以共有36个.
答案:C
二、3.解析:找A关于l的对称点A′,A′B与直线l的交点即为所求的P点.
答案:P(5,6)
4.解析:光线l所在的直线与圆x2+y2-4x-4y+7=0关于x轴对称的圆相切.
答案:3x+4y-3=0或4x+3y+3=0
5.解析:f(θ)=![]() 表示两点(cosθ,sinθ)与(2,1)连线的斜率.
表示两点(cosθ,sinθ)与(2,1)连线的斜率.
答案:![]() 0
0
6.解析:原不等式变为(x2-1)m+(1-2x)<0,构造线段f(m)=(x2-1)m+1-2x,-2≤m≤2,则f(-2)<0,且f(2)<0.
答案:![]()
三、7.(1)证明:设A、B的横坐标分别为x1、x2,由题设知x1>1,x2>1,
点A(x1,log8x1),B(x2,log8x2).
因为A、B在过点O的直线上,所以![]() ,又点C、D的坐标分别为(x1,log2x1)、(x2,log2x2).
,又点C、D的坐标分别为(x1,log2x1)、(x2,log2x2).
由于log2x1=3log8x1,log2x2=3log8x2,则
![]()
由此得kOC=kOD,即O、C、D在同一直线上.
(2)解:由BC平行于x轴,有log2x1=log8x2,又log2x1=3log8x1
∴x2=x13
将其代入![]() ,得x13log8x1=3x1log8x1,
,得x13log8x1=3x1log8x1,
由于x1>1知log8x1≠0,故x13=3x1x2=![]() ,于是A(
,于是A(![]() ,log8
,log8![]() ).
).
9.(1)证明:由条件,得a1=S1=a,当n≥2时,
有an=Sn-Sn-1=[na+n(n-1)b]-[(n-1)a+(n-1)(n-2)b]=a+2(n-1)b.
因此,当n≥2时,有an-an-1=[a+2(n-1)b]-[a+2(n-2)b]=2b.
所以{an}是以a为首项,2b为公差的等差数列.
(2)证明:∵b≠0,对于n≥2,有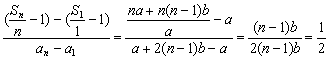
∴所有的点Pn(an,![]() -1)(n=1,2,…)都落在通过P1(a,a-1)且以
-1)(n=1,2,…)都落在通过P1(a,a-1)且以![]() 为斜率的直线上.此直线方程为y-(a-1)=
为斜率的直线上.此直线方程为y-(a-1)= ![]() (x-a),即x-2y+a-2=0.
(x-a),即x-2y+a-2=0.
(3)解:当a=1,b=![]() 时,Pn的坐标为(n,
时,Pn的坐标为(n,![]() ),使P1(1,0)、P2(2,
),使P1(1,0)、P2(2, ![]() )、P3(3,1)都落在圆C外的条件是
)、P3(3,1)都落在圆C外的条件是
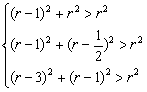
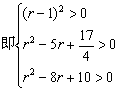
由不等式①,得r≠1
由不等式②,得r<![]() -
-![]() 或r>
或r>![]() +
+![]()
由不等式③,得r<4-![]() 或r>4+
或r>4+![]()
再注意到r>0,1<![]() -
-![]() <4-
<4-![]() =
=![]() +
+![]() <4+
<4+![]()
故使P1、P2、P3都落在圆C外时,r的取值范围是(0,1)∪(1,![]() -
-![]() )∪(4+
)∪(4+![]() ,+∞).
,+∞).
【直线练习2】
1.![]() 的方程为
的方程为![]() ,
,![]() 关于
关于![]() 轴对称的直线为
轴对称的直线为![]() ,
,![]() 关于y轴对称的直线为
关于y轴对称的直线为![]() ,那么直线
,那么直线![]() 的方程为( B )
的方程为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.与圆![]() 相外切,且与
相外切,且与![]() 轴相切的动圆的圆心的轨迹方程是 。
轴相切的动圆的圆心的轨迹方程是 。![]()
3.已知定点A(1,1),B(3,3),点P在x轴上,且![]() 取得最大值,则P点坐标为( B )
取得最大值,则P点坐标为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
解:P点即为过A、B两点且与x轴相切的圆的切点,设圆方程为
![]()
![]()
所以有![]()
4.圆![]() 上的点到直线
上的点到直线![]() 的最知距离为( A )
的最知距离为( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.条件甲:方程![]() 表示一双条双曲线,条件乙:
表示一双条双曲线,条件乙:![]() 则乙是甲的( A )
则乙是甲的( A )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
6.设点P在有向线段![]() 的延长线上,点P分
的延长线上,点P分![]() 所成的比为
所成的比为![]() , 则( A )
, 则( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.如果AC<0且BC<0, 那么直线Ax + By +C = 0, 不通过( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.若点(4, m)到直线![]() 的距离不大于3, 则m的取值范围是( B
)
的距离不大于3, 则m的取值范围是( B
)
A.(0, 10) B.![]() C.
C.![]() D.
D.![]()
9.原点关于直线![]() 的对称点坐标为( D )
的对称点坐标为( D )
A.![]() B.
B.![]() C.(3, 4) D.(4, 3)
C.(3, 4) D.(4, 3)
10.如果直线![]() 与直线
与直线![]() 关于直线y = x对称, 那么( A
)
关于直线y = x对称, 那么( A
)
A.![]() B.
B.![]()
C.a = 3, b = -2 D.a = 3, b = 6
11.已知直线![]() 的夹角的平分线为
的夹角的平分线为![]() , 如果l1的方程是
, 如果l1的方程是![]() ,那么l2
,那么l2
的方程是( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.如果直线![]() 与直线
与直线![]() 平行, 那么系数a = ( B
)
平行, 那么系数a = ( B
)
A.-3 B.-6 C.![]() D.
D.![]()
13.两条直线![]()
![]() 垂直的充要条件是( A )
垂直的充要条件是( A )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
14.如果直线l沿x轴负方向平移3个单位, 再沿y轴正方向平移1个单位, 又回到原来的位置, 那么直线l的斜率是( A )
A.![]() B.-3 C.
B.-3 C.![]() D.3
D.3
15.设a、b、c分别是△ABC中, Ð A、ÐB、ÐC所对边的边长, 则直线![]()
与![]() 的位置关系是( C )
的位置关系是( C )
A.平行 B.重合 C.垂直 D.相交但不垂直
16.求与点A(1, 2)的距离等于4, 且到x轴的距离等于2的点的坐标: 。(3, 2)
17.直线L:y=kx-1与曲线![]() 不相交,则k的取值范围是( A )
不相交,则k的取值范围是( A )
A.![]() 或3 B.
或3 B.![]() C.3 D.[
C.3 D.[![]() ,3]
,3]
18. 2.如果a·c<0,b·c<0,那么直线ax+by+c=0不通过( C )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
19.直线y=-x-1被圆![]() ,所截的弦长为( C )
,所截的弦长为( C )
A.![]() B.40
B.40![]() C.
C.![]() D.
D.![]()
20.斜率为1的直线与两直线2x+y-1=0,![]() 分别相交于A,B两点,线段AB的
分别相交于A,B两点,线段AB的
中点的轨迹方程为( B )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
21.已知双曲线![]() 和椭圆
和椭圆![]() :
:![]() 有公共的焦点,它们的离心率分别是
有公共的焦点,它们的离心率分别是![]() 和
和![]() ,且
,且![]() 。(1)求双曲线
。(1)求双曲线![]() 的方程;(2)圆D经过双曲线
的方程;(2)圆D经过双曲线![]() 的两焦点,且 与x轴有两个交点,这两个交点间的距离等于8,求圆D的方程。
的两焦点,且 与x轴有两个交点,这两个交点间的距离等于8,求圆D的方程。
解:(1)椭圆![]() 的两个焦点坐标是
的两个焦点坐标是![]() 离心率
离心率![]()
由![]() 可知双曲线
可知双曲线![]() 的离心率
的离心率![]()
∴![]()
故双曲线![]() 的方程为
的方程为![]()
(2)∵圆D经过双曲线的两个焦点,∴圆心D在直线x= –2上
设圆D的方程为![]()
整理得:![]()
令y=0,得![]()
设圆D与x轴的两个交点为(![]() ),(
),(![]() ),则
),则
![]()
依题意![]() =
=![]()
即16–4(2b–22)=64,解得b=5
所以圆的方程为![]()
高三数学专题复习
圆
【例题】
【例1】
设正方形ABCD的外接圆方程为x2+y2–6x+a=0(a<9),C、D点所在直线l的斜率为![]() ,求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率。
,求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率。
解:由(x–3)2+y2=9-a(a<9)可知圆心M的坐标为(3,0)
依题意:![]()
MA,MB的斜率k满足: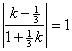
解得:kAC=![]()
【例2】
设圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
(1)求![]() 关于
关于![]() 对称的圆
对称的圆![]() 的方程;
的方程;
(2)当![]() 变化且
变化且![]() 时,求证:
时,求证:![]() 的圆心在一条定直线上,并求
的圆心在一条定直线上,并求![]() 所表示的一系列圆的公切线方程.
所表示的一系列圆的公切线方程.
解:(1)圆C1的圆心为C1(-2,3m+2),设C1关于直线l对称点为C2(a,b)
则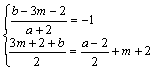 解得:
解得:![]()
∴圆C2的方程为![]()
(2)由![]() 消去m得a-2b+1=0
消去m得a-2b+1=0
即圆C2的圆心在定直线x-2y+1=0上。
设直线y=kx+b与圆系中的所有圆都相切,则
![]()
即![]()
∵直线y=kx+b与圆系中的所有圆都相切,所以上述方程对所有的m值都成立,所以有: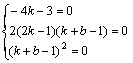 解之得:
解之得: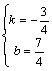
所以![]() 所表示的一系列圆的公切线方程为:
所表示的一系列圆的公切线方程为:![]()
【例3】
已知圆C:![]() ,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在求出直线l的方程,若不存在说明理由。
,是否存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点,若存在求出直线l的方程,若不存在说明理由。
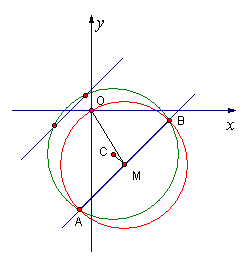 解:圆C化成标准方程为
解:圆C化成标准方程为![]()
假设存在以AB为直径的圆M,圆心M的坐标为(a,b)
由于CM⊥l,∴kCM×kl= -1
∴kCM=![]() ,
,
即a+b+1=0,得b= -a-1 ①
直线l的方程为y-b=x-a,
即x-y+b-a=0
CM=![]()
∵以AB为直径的圆M过原点,∴![]()
![]() ,
,![]()
∴![]() ②
②
把①代入②得 ![]() ,∴
,∴![]()
当![]() 此时直线l的方程为x-y-4=0;
此时直线l的方程为x-y-4=0;
当![]() 此时直线l的方程为x-y+1=0
此时直线l的方程为x-y+1=0
故这样的直线l是存在的,方程为x-y-4=0 或x-y+1=0
【例4】 已知点A(-2,-1)和B(2,3),圆C:x2+y2 = m2,当圆C与线段AB没有公共
点时,求m的取值范围.
解:∵过点A、B的直线方程为在l:x-y+1 = 0,
作OP垂直AB于点P,连结OB.
由图象得:m<OP或m>OB时,线段AB与圆x2+y2 = m2无交点.
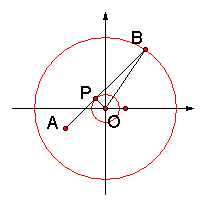 (I)当m<OP时,由点到直线的距离公式得:
(I)当m<OP时,由点到直线的距离公式得:
![]() ,即
,即![]() .
.
(II)当![]() >OB时,
>OB时,
![]() ,
,
即
![]() .
.
∴当![]() 和
和![]() 时,
时,
圆x2+y2 = m2与线段AB无交点.
【例5】
已知⊙M:![]() 轴上的动点,QA,QB分别切⊙M于A,B两点,
轴上的动点,QA,QB分别切⊙M于A,B两点,
(1)如果![]() ,求直线MQ的方程;
,求直线MQ的方程;
(2)求动弦AB的中点P的轨迹方程.
|
由![]() ,
,
可得![]()
由射影定理,得 ![]()
在Rt△MOQ中,
![]() ,
,
故![]() ,所以直线AB方程是
,所以直线AB方程是
![]()
(2)由点M,P,Q在一直线上,
得![]()
由射影定理得![]()
即![]()
把(*)代入(**)消去a,
并注意到![]() ,可得
,可得![]()
【例6】 有一种大型商品,A、B两地都有出售,且价格相同,某地居民从两地之一购得
商品后回运的运费是:每单位距离A地的运费是B地运费的3倍,已知A、B两地相距10km,居民选择A或B地购买这种商品的标准是:包括运费和价格的总费用较低.求A、B两地的售货区域的分界线的曲线形状,并指出曲线上、曲线内、曲线外的居民应如何选择购货地点.
解:以AB所在直线为x轴,线段AB的中点为原点建立直角坐标系,
则A(-5,0),B(5,0).
设某地P的坐标为(x,y),且P地居民选择A地购买商品的费用较低,并设A地的运费为3a元/km,则B地运费为a元/km.
由于P地居民购买商品的总费用满足条件:价格+A地运费≤价格+B地运费 ,
即![]()
![]() ,整理得
,整理得![]() .
.
所以,以点C![]() 为圆心,
为圆心,![]() 为半径的圆就是两地居民购货的分界线.
为半径的圆就是两地居民购货的分界线.
圆内的居民从A地购货费用较低;
圆外的居民从B地购货费用较低;
圆上的居民从A、B两地购货的总费用相等,因此可以随意从A、B两地之一购货.
【例7】
例8、在![]() 平面上有一系列点
平面上有一系列点![]()
![]() 对每个自然数
对每个自然数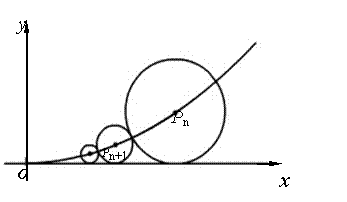
![]() ,点
,点![]() 位于函数
位于函数![]() 的图象上.以点
的图象上.以点![]() 为圆心的⊙
为圆心的⊙![]() 与
与![]() 轴都相切,且⊙
轴都相切,且⊙![]() 与⊙
与⊙![]() 又彼此外切.若
又彼此外切.若![]() ,且
,且![]()
![]() .
.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)设⊙![]() 的面积为
的面积为![]() ,
,![]() ,求证:
,求证:![]()
解:(1)依题意,⊙![]() 的半径
的半径![]() ,
,![]() ⊙
⊙![]() 与⊙
与⊙![]() 彼此外切,
彼此外切,
![]() ,
, ![]() ,
,
两边平方,化简得![]() , 即
, 即![]() .
.
![]() ,
, ![]()
![]() ,
, ![]() .
.
∴ 数列![]() 是等差数列.
是等差数列.
(2) 由题设,![]() ,∴
,∴![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
=![]()
=![]()
![]() .
.
【例8】
已知圆![]() :
:![]() 和圆
和圆![]() :
:![]() ,现在构造一系列的圆
,现在构造一系列的圆![]() ,使圆
,使圆![]() 同时与
同时与![]() 和圆
和圆![]() 都相切,并都与OX轴相切.回答:
都相切,并都与OX轴相切.回答:
(1)求圆![]() 的半径
的半径![]() ;
;
(2)证明:两个相邻圆![]() 和
和![]() 在切点间的公切线长为
在切点间的公切线长为![]() ;
;
(3)求和![]() .
.
解:(1)在直角梯形![]() 中,
中,
AC=1-![]() ,
,![]() =1+
=1+![]() ,
,![]() =1+
=1+![]() ,
,![]()
![]() =
=![]() +
+![]() .
.![]() =
=![]() -
-![]() .
.
∴有![]()
![]() ,
,![]()
![]() ,
,![]() =
=![]()
∴![]()
∴![]() .即
.即![]() .
.
由此可得![]() .
.
∴{![]() }成等差数列,
}成等差数列, ![]() .
.
∴![]() ,∴
,∴![]() .
.
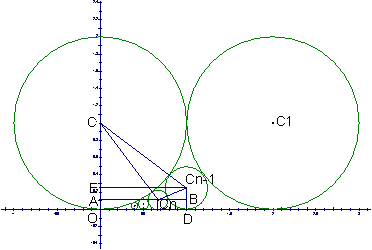
(2)公切线长为![]()
![]() .
.
(3) ![]()
![]() =
=![]() .
.
∴![]() =2.
=2.
【圆·练习】
一、选择题
1、直线![]() 绕原点按顺时针方向旋转30°所得直线与圆
绕原点按顺时针方向旋转30°所得直线与圆![]() 的位置关系是
( ).
的位置关系是
( ).
(A)直线与圆相切 (B) 直线与圆相交但不过圆心
(C)直线与圆相离 (D) 直线过圆心
2、点![]() 是圆
是圆![]() 内不为圆心的一点,则直线
内不为圆心的一点,则直线![]() 与该圆的位置关系是
( )
与该圆的位置关系是
( )
A.相切 B.相交 C.相离 D.相切或相交
3、直线![]() 截圆
截圆![]() 所得弦长等于4,则以a、b、c为边长的确良三角形一定是 ( )
所得弦长等于4,则以a、b、c为边长的确良三角形一定是 ( )
(A)直角三角形 (B)锐角三角形 (C)钝角三角形 (D)不存在
4、已知两点A(–2,0),B(0,2), 点C是圆x2+y2–2x=0上的任意一点,则△ABC面积的最小值是( )
(A)![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
5、已知集合![]() 及
及![]() ,则实数b的取值范围是 ( )
,则实数b的取值范围是 ( )
(A)[–5,5] (B)![]() (C)
(C)![]() (D)
(D)![]()
6、若曲线x2+y2+a2x=(1–a2)y–4=0关于直线y–x=0的对称曲线仍是其本身,则实数a=( ).
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7、若圆![]() 上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是
( ).
上有且仅有两个点到直线4x+3y=11的距离等于1,则半径R的取值范围是
( ).
(A)R>1 (B)R<3 (C)1<R<3 (D)R≠2
二、填空题
8、已知圆![]() 交于A、B两点,则AB所在的直线方程是_______________________。
交于A、B两点,则AB所在的直线方程是_______________________。
9、直线![]() 上的点到圆
上的点到圆![]() 的最近距离是
。
的最近距离是
。
10、已知圆的方程是x2+y2=1,则在y轴上截距为![]() 的切线方程为
。
的切线方程为
。
11、过P(-2,4)及Q(3,-1)两点,且在X轴上截得的弦长为6的圆方程是
三、解答题
12、半径为5的圆过点A(-2, 6),且以M(5, 4)为中点的弦长为2![]() ,求此圆的方程。
,求此圆的方程。
13、已知圆![]() 与y轴交于A、B两点,圆心为P,若
与y轴交于A、B两点,圆心为P,若![]() 。
。
求m的值。
14、已知定点![]() ,
,![]() 点在圆
点在圆![]() 上运动,
上运动,![]() 的平分线交
的平分线交![]() 于
于![]() 点,其中
点,其中![]() 为坐标原点,求
为坐标原点,求![]() 点的轨迹方程.
点的轨迹方程.
【圆参考答案】
一、选择题
1、A 2、C 3、A 4、A 5、C 6、B 7、C
二、填空题
8、2x+y=0 9、![]() 10、
10、![]()
11、(x-1)2+(y-2)2=13或(x-3)2+(y-4)2=25
三、解答题
12、解:设圆心坐标为P(a, b), 则圆的方程是(x-a)2+(y-b)2=25,
∵ (-2, 6)在圆上,∴ (a+2)2+(b-6)2=25, 又以M(5, 4)为中点的弦长为2![]() ,
,
∴ PM2=r2-![]() 2, 即(a-5)2+(b-4)2=20,
2, 即(a-5)2+(b-4)2=20,
联立方程组![]() , 两式相减得7a-2b=3, 将b=
, 两式相减得7a-2b=3, 将b=![]() 代入
代入
得 53a2-194a+141=0, 解得a=1或a=![]() , 相应的求得b1=2, b2=
, 相应的求得b1=2, b2=![]() ,
,
∴ 圆的方程是(x-1)2+(y-2)2=25或(x-![]() )2+(y-
)2+(y-![]() )2=25
)2=25
13、解:由题设△APB是等腰直角三角形,∴圆心到y轴的距离是圆半径的![]() 倍
倍
将圆方程![]() 配方得:
配方得:![]()
圆心是P(2,-1),半径r=![]()
 ∴
∴![]() 解得m= -3
解得m= -3
14、解:在△AOP中,∵OQ是ÐAOP的平分线
∴![]()
设Q点坐标为(x,y);P点坐标为(x0,y0)
∴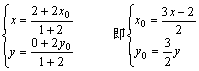
∵ P(x0,y0)在圆x2+y2=1上运动,∴x02+y02=1
即![]() ∴
∴![]()
此即Q点的轨迹方程。