08高考数学第二轮复习直线和平面
一、考纲要求
1.掌握平面的基本性质,空间两条直线、直线和平面、两个平面的位置关系(特别是平行和垂直关系)以及它们所成的角与距离的概念.
2.对于异面直线的距离,只要求会计算已给出公垂线时的距离.
3.能运用上述概念以及有关两条直线、直线和平面、两个平面的平行和垂直关系的性质与判定,进行论证和解决有关问题.
4.会用斜二侧的画法画水平放置的平面图形(特别是正三角形、正四边形、正五边形、两个平面、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系.
5.理解用反证法证明命题的思路,会用反证法证明一些简单的问题.
二、知识结构
1.空间多边形不在同一平面内的若干线段首尾相接所成的图形叫做空间折线.
若空间折线的最后一条线段的尾端与最初一条线段的首端重合,则叫做封闭的空间折线.
若封闭的空间折线各线段彼此不相交,则叫做这空间多边形平面,平面是一个不定义的概念,几何里的平面是无限伸展的.
平面通常用一个平行四边形来表示.
平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母表示,如平面AC.
在立体几何中,大写字母A,B,C,…表示点,小写字母,a,b,c,…l,m,n,…表示直线,且把直线和平面看成点的集合,因而能借用集合论中的符号表示它们之间的关系,例如:
A∈l—点A在直线l上;
A![]() α—点A不在平面α内;
α—点A不在平面α内;
l![]() α—直线l在平面α内;
α—直线l在平面α内;
a![]() α—直线a不在平面α内;
α—直线a不在平面α内;
l∩m=A—直线l与直线m相交于A点;
α∩l=A—平面α与直线l交于A点;
α∩β=l—平面α与平面β相交于直线l.
2.平面的基本性质
公理1 如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在这个平面内.
公理2 如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.
公理3 经过不在同一直线上的三个点,有且只有一个平面.
根据上面的公理,可得以下推论.
推论1 经过一条直线和这条直线外一点,有且只有一个平面.
推论2 经过两条相交直线,有且只有一个平面.
推论3 经过两条平行直线,有且只有一个平面.
|
|
|
![]()
|
|
4.空间线面的位置关系
![]()
![]() 平行—没有公共点
平行—没有公共点
共面
(1)直线与直线 相交—有且只有一个公共点
异面(既不平行,又不相交)
![]() 直线在平面内—有无数个公共点
直线在平面内—有无数个公共点
![]() (2)直线和平面 直线不在平面内 平行—没有公共点
(2)直线和平面 直线不在平面内 平行—没有公共点
(直线在平面外) 相交—有且只有一个公共点
![]() 相交—有一条公共直线(无数个公共点)
相交—有一条公共直线(无数个公共点)
(3)平面与平面
平行—没有公共点
5.异面直线的判定
证明两条直线是异面直线通常采用反证法.
有时也可用定理“平面内一点与平面外一点的连线,与平面内不经过该点的直线是异面直线”.
6.线面平行与垂直的判定
(1)两直线平行的判定
①定义:在同一个平面内,且没有公共点的两条直线平行.
②如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,即若a∥α,aβ,α∩β=b,则a∥b.
③平行于同一直线的两直线平行,即若a∥b,b∥c,则a∥c.
④垂直于同一平面的两直线平行,即若a⊥α,b⊥α,则a∥b
⑤两平行平面与同一个平面相交,那么两条交线平行,即若α∥β,α∩γ,β∩γ=b,则a∥b
⑥如果一条直线和两个相交平面都平行,那么这条直线与这两个平面的交线平行,即若α∩β=b,a∥α,a∥β,则a∥b.
(2)两直线垂直的判定
①定义:若两直线成90°角,则这两直线互相垂直.
②一条直线与两条平行直线中的一条垂直,也必与另一条垂直.即若b∥c,a⊥b,则a⊥c
③一条直线垂直于一个平面,则垂直于这个平面内的任意一条直线.即若a⊥α,b![]() α,a⊥b.
α,a⊥b.
④三垂线定理和它的逆定理:在平面内的一条直线,若和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直.
⑤如果一条直线与一个平面平行,那么这条直线与这个平面的垂线垂直.即若a∥α,b⊥α,则a⊥b.
⑥三个两两垂直的平面的交线两两垂直,即若α⊥β,β⊥γ,γ⊥α,且α∩β=a,β∩γ=b,γ∩α=c,则a⊥b,b⊥c,c⊥a.
(3)直线与平面平行的判定
①定义:若一条直线和平面没有公共点,则这直线与这个平面平行.
②如果平面外一条直线和这个平面内的一条直线平行,则这条直线与这个平面平行.即若a![]() α,b
α,b![]() α,a∥b,则a∥α.
α,a∥b,则a∥α.
③两个平面平行,其中一个平面内的直线平行于另一个平面,即若α∥β,l![]() α,则l∥β.
α,则l∥β.
④如果一个平面和平面外的一条直线都垂直于同一平面,那么这条直线和这个平面平行.即若α⊥β,l⊥β,l![]() α,则l∥α.
α,则l∥α.
⑤在一个平面同侧的两个点,如果它们与这个平面的距离相等,那么过这两个点的直线与这个平面平行,即若A![]() α,B
α,B![]() α,A、B在α同侧,且A、B到α等距,则AB∥α.
α,A、B在α同侧,且A、B到α等距,则AB∥α.
⑥两个平行平面外的一条直线与其中一个平面平行,也与另一个平面平行,即若α∥β,a![]() α,a
α,a![]() β,a∥α,则α∥β.
β,a∥α,则α∥β.
⑦如果一条直线与一个平面垂直,则平面外与这条直线垂直的直线与该平面平行,即若a⊥α,b![]() α,b⊥a,则b∥α.
α,b⊥a,则b∥α.
⑧如果两条平行直线中的一条平行于一个平面,那么另一条也平行于这个平面(或在这个平面内),即若a∥b,a∥α,b∥α(或b![]() α)
α)
(4)直线与平面垂直的判定
①定义:若一条直线和一个平面内的任何一条直线垂直,则这条直线和这个平面垂直.
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.即若m![]() α,n
α,n![]() α,m∩n=B,l⊥m,l⊥n,则l⊥α.
α,m∩n=B,l⊥m,l⊥n,则l⊥α.
③如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.即若l∥a,a⊥α,则l⊥α.
④一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面,即若α∥β,l⊥β,则l⊥α.
⑤如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面,即若α⊥β,a∩β=α,l![]() β,l⊥a,则l⊥α.
β,l⊥a,则l⊥α.
⑥如果两个相交平面都垂直于第三个平面,则它们的交线也垂直于第三个平面,即若α⊥γ,β⊥γ,且a∩β=α,则a⊥γ.
(5)两平面平行的判定
①定义:如果两个平面没有公共点,那么这两个平面平行,即无公共点![]() α∥β.
α∥β.
②如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行,即若a,b![]() α,a∩b=P,a∥β,b∥β,则α∥β.
α,a∩b=P,a∥β,b∥β,则α∥β.
③垂直于同一直线的两平面平行.即若α⊥a,β⊥a,则α∥β.
④平行于同一平面的两平面平行.即若α∥β,β∥γ,则α∥γ.
⑤一个平面内的两条直线分别平行于另一平面内的两条相交直线,则这两个平面平行,即若a,b![]() α,c,d
α,c,d![]() β,a∩b=P,a∥c,b∥d,则α∥β.
β,a∩b=P,a∥c,b∥d,则α∥β.
(6)两平面垂直的判定
①定义:两个平面相交,如果所成的二面角是直二面角,那么这两个平面互相垂直,即二面角α-a-β=90°![]() α⊥β.
α⊥β.
②如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直,即若l⊥β,l![]() α,则α⊥β.
α,则α⊥β.
③一个平面垂直于两个平行平面中的一个,也垂直于另一个.即若α∥β,α⊥γ,则β⊥γ.
7.直线在平面内的判定
(1)利用公理1:一直线上不重合的两点在平面内,则这条直线在平面内.
(2)若两个平面互相垂直,则经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内,即若α⊥β,A∈α,AB⊥β,则AB![]() α.
α.
(3)过一点和一条已知直线垂直的所有直线,都在过此点而垂直于已知直线的平面内,即若A∈a,a⊥b,A∈α,b⊥α,则a![]() α.
α.
(4)过平面外一点和该平面平行的直线,都在过此点而与该平面平行的平面内,即若P![]() α,P∈β,β∥α,P∈a,a∥α,则a
α,P∈β,β∥α,P∈a,a∥α,则a![]() β.
β.
(5)如果一条直线与一个平面平行,那么过这个平面内一点与这条直线平行的直线必在这个平面内,即若a∥α,A∈α,A∈b,b∥a,则b![]() α.
α.
8.存在性和唯一性定理
(1)过直线外一点与这条直线平行的直线有且只有一条;
(2)过一点与已知平面垂直的直线有且只有一条;
(3)过平面外一点与这个平面平行的平面有且只有一个;
(4)与两条异面直线都垂直相交的直线有且只有一条;
(5)过一点与已知直线垂直的平面有且只有一个;
(6)过平面的一条斜线且与该平面垂直的平面有且只有一个;
(7)过两条异面直线中的一条而与另一条平行的平面有且只有一个;
(8)过两条互相垂直的异面直线中的一条而与另一条垂直的平面有且只有一个.
9.射影及有关性质
(1)点在平面上的射影自一点向平面引垂线,垂足叫做这点在这个平面上的射影,点的射影还是点.
(2)直线在平面上的射影自直线上的两个点向平面引垂线,过两垂足的直线叫做直线在这平面上的射影.
和射影面垂直的直线的射影是一个点;不与射影面垂直的直线的射影是一条直线.
(3)图形在平面上的射影一个平面图形上所有的点在一个平面上的射影的集合叫做这个平面图形在该平面上的射影.
当图形所在平面与射影面垂直时,射影是一条线段;
当图形所在平面不与射影面垂直时,射影仍是一个图形.
(4)射影的有关性质
从平面外一点向这个平面所引的垂线段和斜线段中:
(i)射影相等的两条斜线段相等,射影较长的斜线段也较长;
(ii)相等的斜线段的射影相等,较长的斜线段的射影也较长;
(iii)垂线段比任何一条斜线段都短.
10.空间中的各种角
等角定理及其推论
定理若一个角的两边和另一个角的两边分别平行,并且方向相同,则这两个角相等.
推论若两条相交直线和另两条相交直线分别平行,则这两组直线所成的锐角(或直角)相等.
异面直线所成的角
(1)定义:a、b是两条异面直线,经过空间任意一点O,分别引直线a′∥a,b′∥b,则a′和b′所成的锐角(或直角)叫做异面直线a和b所成的角.
(2)取值范围:0°<θ≤90°.
(3)求解方法
①根据定义,通过平移,找到异面直线所成的角θ;
②解含有θ的三角形,求出角θ的大小.
11.直线和平面所成的角
(1)定义 和平面所成的角有三种:
(i)垂线 面所成的角 的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.
(ii)垂线与平面所成的角 直线垂直于平面,则它们所成的角是直角.
(iii)一条直线和平面平行,或在平面内,则它们所成的角是0°的角.
(2)取值范围0°≤θ≤90°
(3)求解方法
①作出斜线在平面上的射影,找到斜线与平面所成的角θ.
②解含θ的三角形,求出其大小.
③最小角定理
斜线和平面所成的角,是这条斜线和平面内经过斜足的直线所成的一切角中最小的角,亦可说,斜线和平面所成的角不大于斜线与平面内任何直线所成的角.
12.二面角及二面角的平面角
(1)半平面 直线把平面分成两个部分,每一部分都叫做半平面.
(2)二面角 条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱,这两个平面叫做二面角的面,即二面角由半平面一棱一半平面组成.
若两个平面相交,则以两个平面的交线为棱形成四个二面角.
二面角的大小用它的平面角来度量,通常认为二面角的平面角θ的取值范围是
0°<θ≤180°
(3)二面角的平面角
①以二面角棱上任意一点为端点,分别在两个面内作垂直于棱的射线,这两条射线所组成的角叫做二面角的平面角.
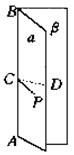
如图,∠PCD是二面角α-AB-β的平面角.平面角∠PCD的大小与顶点C在棱AB上的位置无关.
②二面角的平面角具有下列性质:
(i)二面角的棱垂直于它的平面角所在的平面,即AB⊥平面PCD.
 (ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.
(ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线,垂足必在平面角的另一边(或其反向延长线)上.
(iii)二面角的平面角所在的平面与二面角的两个面都垂直,即平面PCD⊥α,平面PCD⊥β.
③找(或作)二面角的平面角的主要方法.
(i)定义法
(ii)垂面法
(iii)三垂线法
(Ⅳ)根据特殊图形的性质
(4)求二面角大小的常见方法
①先找(或作)出二面角的平面角θ,再通过解三角形求得θ的值.
②利用面积射影定理
S′=S·cosα
其中S为二面角一个面内平面图形的面积,S′是这个平面图形在另一个面上的射影图形的面积,α为二面角的大小.
③利用异面直线上两点间的距离公式求二面角的大小.
13.空间的各种距离
点到平面的距离
(1)定义 面外一点引一个平面的垂线,这个点和垂足间的距离叫做这个点到这个平面的距离.
(2)求点面距离常用的方法:
1)直接利用定义求
①找到(或作出)表示距离的线段;
②抓住线段(所求距离)所在三角形解之.
2)利用两平面互相垂直的性质.即如果已知点在已知平面的垂面上,则已知点到两平面交线的距离就是所求的点面距离.
3)体积法其步骤是:①在平面内选取适当三点,和已知点构成三棱锥;②求出此三棱锥的体积V和所取三点构成三角形的面积S;③由V=![]() S·h,求出h即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.
S·h,求出h即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.
4)转化法将点到平面的距离转化为(平行)直线与平面的距离来求.
14.直线和平面的距离
(1)定义一条直线和一个平面平行,这条直线上任意一点到平面的距离,叫做这条直线和平面的距离.
(2)求线面距离常用的方法
①直接利用定义求证(或连或作)某线段为距离,然后通过解三角形计算之.
②将线面距离转化为点面距离,然后运用解三角形或体积法求解之.
③作辅助垂直平面,把求线面距离转化为求点线距离.
15.平行平面的距离
(1)定义 个平行平面同时垂直的直线,叫做这两个平行平面的公垂线.公垂线夹在两个平行平面间的部分,叫做这两个平行平面的公垂线段.两个平行平面的公垂线段的长度叫做这两个平行平面的距离.
(2)求平行平面距离常用的方法
①直接利用定义求
证(或连或作)某线段为距离,然后通过解三角形计算之.
②把面面平行距离转化为线面平行距离,再转化为线线平行距离,最后转化为点线(面)距离,通过解三角形或体积法求解之.
16.异面直线的距离
(1)定义 条异面直线都垂直相交的直线叫做两条异面直线的公垂线.两条异面直线的公垂线在这两条异面直线间的线段的长度,叫做两条异面直线的距离.
任何两条确定的异面直线都存在唯一的公垂线段.
(2)求两条异面直线的距离常用的方法
①定义法 题目所给的条件,找出(或作出)两条异面直线的公垂线段,再根据有关定理、性质求出公垂线段的长.
此法一般多用于两异面直线互相垂直的情形.
②转化法 为以下两种形式:线面距离面面距离
③等体积法
④最值法
⑤射影法
⑥公式法
直线与平面
【例题】
【例1】
 正三棱锥P-ABC的高和底面边长都等于a,EF是PA与BC的公垂线,E、F分别是垂足。(1)求证:侧棱PA^截面BEC (2)求截面BEC的面积;(3)求截面BEC与底面ABC所成二面角的大小
正三棱锥P-ABC的高和底面边长都等于a,EF是PA与BC的公垂线,E、F分别是垂足。(1)求证:侧棱PA^截面BEC (2)求截面BEC的面积;(3)求截面BEC与底面ABC所成二面角的大小
解:1)略
2)易知F为BC的中点,在RtΔPAO中,AO=![]() ,PO=a,
,PO=a,
所以PA=![]() ,又易知PA⊥BE,
,又易知PA⊥BE,
在等腰三角形PAB中,可求得BE=![]() ,
,
所以在直角三角形EFB中,求得EF=![]() ,所以
,所以![]()
3)∠EFA=300
【例2】 已知斜三棱柱ABC—A1B1C1中,A1C1=B1C1=2,D、D1分别是AB、A1B1的中点,平面A1ABB1⊥平面A1B1C1,异面直线AB1和C1B互相垂直.
(1)求证:AB1⊥C1D1;
(2)求证:AB1⊥面A1CD;
(3)若AB1=3,求直线AC与平面A1CD所成的角.
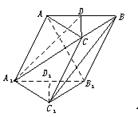
解:(1)证明:∵A1C1=B1C1,D1是A1B1的中点,∴C1D1⊥A1B1于D1,
又∵平面A1ABB1⊥平面A1B1C1,∴C1D1⊥平面A1B1BA,
而AB1![]() 平面A1ABB1,∴AB1⊥C1D1.
平面A1ABB1,∴AB1⊥C1D1.
(2)证明:连结D1D,∵D是AB中点,∴DD1![]() CC1,∴C1D1∥CD,由(1)得CD⊥AB1,又∵C1D1⊥平面A1ABB1,C1B⊥AB1,由三垂线定理得BD1⊥AB1,
CC1,∴C1D1∥CD,由(1)得CD⊥AB1,又∵C1D1⊥平面A1ABB1,C1B⊥AB1,由三垂线定理得BD1⊥AB1,
又∵A1D∥D1B,∴AB1⊥A1D而CD∩A1D=D,∴AB1⊥平面A1CD.
(3)解:由(2)AB1⊥平面A1CD于O,连结CO1得∠ACO为直线AC与平面A1CD所成的角,∵AB1=3,AC=A1C1=2,∴AO=1,∴sinOCA=![]() ,
,
∴∠OCA=![]() .
.
【例3】 两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=FN,求证:MN∥平面BCE.
证法一:作MP⊥BC,NQ⊥BE,P、Q为垂足,则MP∥AB,NQ∥AB.
∴MP∥NQ,又AM=NF,AC=BF,
∴MC=NB,∠MCP=∠NBQ=45°
∴Rt△MCP≌Rt△NBQ
∴MP=NQ,故四边形MPQN为平行四边形
∴MN∥PQ
∵PQ![]() 平面BCE,MN在平面BCE外,
平面BCE,MN在平面BCE外,
∴MN∥平面BCE.
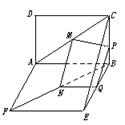
证法二:如图过M作MH⊥AB于H,则MH∥BC,
∴![]()
 连结NH,由BF=AC,FN=AM,得
连结NH,由BF=AC,FN=AM,得![]()
![]() ,
,
由![]()
∴MN∥平面BCE.
【例4】 在斜三棱柱A1B1C1—ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
(1)若D是BC的中点,求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请你叙述判断理由.
解: (1)证明:∵AB=AC,D是BC的中点,∴AD⊥BC
∵底面ABC⊥平面BB1C1C,∴AD⊥侧面BB1C1C
∴AD⊥CC1.
(2)证明:延长B1A1与BM交于N,连结C1N
∵AM=MA1,∴NA1=A1B1
∵A1B1=A1C1,∴A1C1=A1N=A1B1
∴C1N⊥C1B1
∵底面NB1C1⊥侧面BB1C1C,∴C1N⊥侧面BB1C1C
∴截面C1NB⊥侧面BB1C1C
∴截面MBC1⊥侧面BB1C1C.
(3)解:结论是肯定的,充分性已由(2)证明,下面证必要性.
过M作ME⊥BC1于E,∵截面MBC1⊥侧面BB1C1C
∴ME⊥侧面BB1C1C,又∵AD⊥侧面BB1C1C.
∴ME∥AD,∴M、E、D、A共面
∵AM∥侧面BB1C1C,∴AM∥DE
∵CC1⊥AM,∴DE∥CC1
∵D是BC的中点,∴E是BC1的中点
∴AM=DE=![]() AA1,∴AM=MA1.
AA1,∴AM=MA1.
【例5】
 已知斜三棱柱ABC-A’B’C’的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),B’在底面上的射影D落在BC上。
已知斜三棱柱ABC-A’B’C’的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),B’在底面上的射影D落在BC上。
(1)求证:AC⊥面BB’C’C。
(2)当α为何值时,AB’⊥BC’,且使得D恰为BC的中点。
解:(1)∵ B’D⊥面ABC,AC![]() 面ABC,
面ABC,
∴ B’D⊥AC,
又AC⊥BC,BC∩B’D=D,
∴ AC⊥面BB’C’C。
(2)由三垂线定理知道:要使AB’⊥BC’,需且只需AB’在面BB’C’C内的射影B’C⊥BC’。即四边形BB’C’C为菱形。此时,BC=BB’。
因为B’D⊥面ABC,所以,![]() 就是侧棱B’B与底面ABC所成的角。
就是侧棱B’B与底面ABC所成的角。
由D恰好落在BC上,且为BC的中点,所以,此时![]() =
=![]() 。
。
即当α=![]() 时,AB’⊥BC’,且使得D恰为BC的中点。
时,AB’⊥BC’,且使得D恰为BC的中点。
【例6】
 如图:已知四棱锥
如图:已知四棱锥![]() 中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC中点。
中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC中点。
(1)求证:平面EDB⊥平面PBC;
(2)求二面角![]() 的平面角的正切值。
的平面角的正切值。
解:(1)要证两个平面互相垂直,常规的想法是:证明其中一个平面过另一个平面的一条垂线。
首先观察图中已有的直线,不难发现,由于侧面PDC为正三角形,所以,![]() ,那么我们自然想到:是否有
,那么我们自然想到:是否有![]() ?这样的想法一经产生,证明它并不是一件困难的事情。
?这样的想法一经产生,证明它并不是一件困难的事情。
∵ 面PDC⊥底面ABCD,交线为DC,
∴ DE在平面ABCD内的射影就是DC。
在正方形ABCD中,DC⊥CB,
∴ DE⊥CB。
又![]() ,
,![]() ,
,
∴ DE⊥![]() 。
。
又![]() 面EDB,
面EDB,
∴ 平面EDB⊥平面PBC。
(2)由(1)的证明可知:DE⊥![]() 。所以,
。所以,![]() 就是二面角
就是二面角![]() 的平面角。
的平面角。
∵ 面PDC⊥底面ABCD,交线为DC,
又平面ABCD内的直线CB⊥ DC。
∴ CB⊥面PDC。
又![]() 面PDC,
面PDC,
∴ CB⊥PC。
在Rt![]() 中,
中,![]() 。
。

【例7】
如图:在四棱锥![]() 中,
中,![]() ⊥平面
⊥平面![]() ,∠
,∠![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
(1)求证:![]() 平面
平面![]() ;
;
(2)当点![]() 到平面
到平面![]() 的距离为多少时,平面
的距离为多少时,平面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() ?
?
 解:题目中涉及到平面
解:题目中涉及到平面![]() 与平面
与平面![]() 所成的二面角,所以,应作出这两个平面的交线(即二面角的棱)。另一方面,要证
所成的二面角,所以,应作出这两个平面的交线(即二面角的棱)。另一方面,要证![]() 平面
平面![]() ,应该设法证明CE平行于面
,应该设法证明CE平行于面![]() 内的一条直线,充分利用中点(中位线)的性质,不难发现,刚刚做出的二面角的棱正好符合要求。
内的一条直线,充分利用中点(中位线)的性质,不难发现,刚刚做出的二面角的棱正好符合要求。
(1)延长BC、AD交于点F。
在![]() 中,∠
中,∠![]() ,所以,AB、CD都与AF垂直,所以,CD//AB,所以,
,所以,AB、CD都与AF垂直,所以,CD//AB,所以,![]() ∽
∽![]() 。又
。又![]() ,
,![]() ,所以,点D、C分别为线段AF、BF的中点。
,所以,点D、C分别为线段AF、BF的中点。
又因为![]() 为
为![]() 的中点,所以,EC为
的中点,所以,EC为![]() 的中位线,所以,EC//SF。
的中位线,所以,EC//SF。
又![]() ,
,![]() ,所以,
,所以,![]() 平面
平面![]() 。
。
(2)因为:![]() ⊥平面
⊥平面![]() ,AB
,AB![]() 平面
平面![]() ,所以,AB
,所以,AB![]()
![]() 。又AB
。又AB![]() AF,
AF,![]() ,所以,AB
,所以,AB![]() 面
面![]() 。
。
过A作AH![]() SF于H,连BH,则BH
SF于H,连BH,则BH![]() SF,所以,
SF,所以,![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成的二面角的平面角。
所成的二面角的平面角。
在Rt![]() 中,要使
中,要使![]() =
=![]() ,需且只需AH=AB=
,需且只需AH=AB=![]() 。
。
此时,在![]() SAF中,
SAF中,![]() ,所以,
,所以,![]() 。
。
在三棱锥S-ACD中,设点A到面SCD的距离为h,则
h=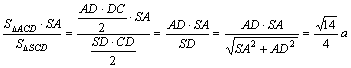
因为AB//DC,所以,AB//面SCD。所以,点A、B到面SCD的距离相等。又因为E为SB中点,所以,点E到平面SCD的距离就等于点B到面SCD距离的一半,即![]() 。
。
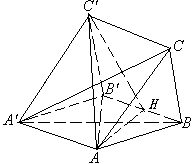
【例8】
如图,在三棱柱![]() 中,四边形
中,四边形![]() 是菱形,四边形
是菱形,四边形![]() 是矩形,
是矩形,![]() 。(1)求证:平面
。(1)求证:平面![]() ;
;
(2)若![]() ,
,
求AC'与平面BCC'所成角的大小(用反三角函数表示)
 解:(1)证明:
解:(1)证明:
∵在三棱柱![]() 中,
中,![]()
∴CB⊥AB;又∵CB⊥![]() ;
;![]()
∴![]()
![]()
(2)解:由![]()
过点A作AH⊥平面![]() ,H为垂足,
,H为垂足,
则H在![]() 上,
上,
连结![]()
连接![]()
可知![]()

因此,直线![]() 与平面
与平面![]() 所成的角是
所成的角是![]() 。
。
【例9】
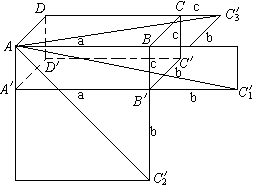 在长方体
在长方体![]() 中,AB=a,
中,AB=a,![]() ,
,![]() ;
;![]() ,由顶点A沿着长方体的表面到顶点
,由顶点A沿着长方体的表面到顶点![]() 的最短距离是多少?
的最短距离是多少?
解:如图所示
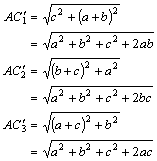
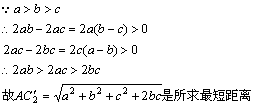
【直线与平面练习】
一、选择题
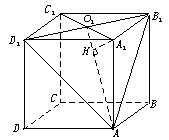
1.在长方体ABCD—A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.在直二面角α—l—β中,直线a![]() α,直线b
α,直线b![]() β,a、b与l斜交,则( )
β,a、b与l斜交,则( )
A.a不和b垂直,但可能a∥b B.a可能和b垂直,也可能a∥b
C.a不和b垂直,a也不和b平行 D.a不和b平行,但可能a⊥b
二、填空题
3.设X、Y、Z是空间不同的直线或平面,对下面四种情形,使“X⊥Z且Y⊥Z![]() X∥Y”为真命题的是_________(填序号).
X∥Y”为真命题的是_________(填序号).
①X、Y、Z是直线 ②X、Y是直线,Z是平面 ③Z是直线,X、Y是平面 ④X、Y、Z是平面
4.设a,b是异面直线,下列命题正确的是_________.
①过不在a、b上的一点P一定可以作一条直线和a、b都相交
②过不在a、b上的一点P一定可以作一个平面和a、b都垂直
③过a一定可以作一个平面与b垂直
④过a一定可以作一个平面与b平行
三、解答题
5.如图,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.
(1)求证:CD⊥PD;
(2)求证:EF∥平面PAD;
(3)当平面PCD与平面ABCD成多大角时,直线EF⊥平面PCD?
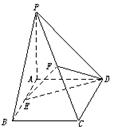
6.如图,在正三棱锥A—BCD中,∠BAC=30°,AB=a,平行于AD、BC的截面EFGH分别交AB、BD、DC、CA于点E、F、G、H.
(1)判定四边形EFGH的形状,并说明理由.
(2)设P是棱AD上的点,当AP为何值时,平面PBC⊥平面EFGH,请给出证明.
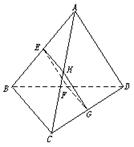
7.如图,正三棱柱ABC—A1B1C1的各棱长都相等,D、E分别是CC1和AB1的中点,点F在BC上且满足BF∶FC=1∶3.
(1)若M为AB中点,求证:BB1∥平面EFM;
(2)求证:EF⊥BC;
(3)求二面角A1—B1D—C1的大小.
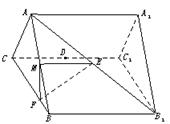
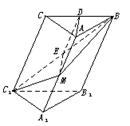
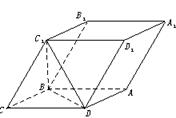
8.如图,已知平行六面体ABCD—A1B1C1D1的底面是菱形且∠C1CB=
∠C1CD=∠BCD=60°,
(1)证明:C1C⊥BD;
(2)假定CD=2,CC1=![]() ,记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值;
,记面C1BD为α,面CBD为β,求二面角α—BD—β的平面角的余弦值;
(3)当![]() 的值为多少时,可使A1C⊥面C1BD?
的值为多少时,可使A1C⊥面C1BD?
参考答案
一、1.解析:如图,设A1C1∩B1D1=O1,∵B1D1⊥A1O1,B1D1⊥AA1,∴B1D1⊥平面AA1O1,故平面AA1O1⊥AB1D1,交线为AO1,在面AA1O1内过A1作A1H⊥AO1于H,则易知A1H长即是点A1到平面AB1D1的距离,在Rt△A1O1A中,A1O1=![]() ,AO1=3
,AO1=3![]() ,由A1O1·A1A=h·AO1,可得A1H=
,由A1O1·A1A=h·AO1,可得A1H=![]() .
.
答案:C
2.解析:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,
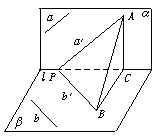
∴△APB为直角三角形,故∠APB为锐角.
答案:C
二、3.解析:①是假命题,直线X、Y、Z位于正方体的三条共点棱时为反例,②③是真命题,④是假命题,平面X、Y、Z位于正方体的三个共点侧面时为反例.
答案:②③
4.④
三、5.证明:(1)∵PA⊥底面ABCD,∴AD是PD在平面ABCD内的射影,
∵CD![]() 平面ABCD且CD⊥AD,∴CD⊥PD.
平面ABCD且CD⊥AD,∴CD⊥PD.
(2)取CD中点G,连EG、FG,
∵E、F分别是AB、PC的中点,∴EG∥AD,FG∥PD
∴平面EFG∥平面PAD,故EF∥平面PAD
(3)解:当平面PCD与平面ABCD成45°角时,直线EF⊥面PCD
证明:G为CD中点,则EG⊥CD,由(1)知FG⊥CD,故∠EGF为平面PCD与平面ABCD所成二面角的平面角.即∠EGF=45°,从而得∠ADP=45°,AD=AP
由Rt△PAE≌Rt△CBE,得PE=CE
又F是PC的中点,∴EF⊥PC,由CD⊥EG,CD⊥FG,得CD⊥平面EFG,CD⊥EF即EF⊥CD,故EF⊥平面PCD.
6.(1)证明:
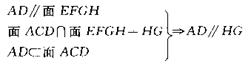
同理EF∥FG,∴EFGH是平行四边形
∵A—BCD是正三棱锥,∴A在底面上的射影O是△BCD的中心,
∴DO⊥BC,∴AD⊥BC,
∴HG⊥EH,四边形EFGH是矩形.
(2)作CP⊥AD于P点,连结BP,∵AD⊥BC,∴AD⊥面BCP
∵HG∥AD,∴HG⊥面BCP,HG![]() 面EFGH.面BCP⊥面EFGH,
面EFGH.面BCP⊥面EFGH,
在Rt△APC中,∠CAP=30°,AC=a,∴AP=![]() a.
a.
7.(1)证明:连结EM、MF,∵M、E分别是正三棱柱的棱AB和AB1的中点,
∴BB1∥ME,又BB1![]() 平面EFM,∴BB1∥平面EFM.
平面EFM,∴BB1∥平面EFM.
(2)证明:取BC的中点N,连结AN由正三棱柱得:AN⊥BC,
又BF∶FC=1∶3,∴F是BN的中点,故MF∥AN,
∴MF⊥BC,而BC⊥BB1,BB1∥ME.
∴ME⊥BC,由于MF∩ME=M,∴BC⊥平面EFM,
又EF平面EFM,∴BC⊥EF.
(3)解:取B1C1的中点O,连结A1O知,A1O⊥面BCC1B1,由点O作B1D的垂线OQ,垂足为Q,连结A1Q,由三垂线定理,A1Q⊥B1D,故∠A1QD为二面角A1—B1D—C的平面角,易得∠A1QO=arctan![]() .
.
8.(1)证明:连结A1C1、AC,AC和BD交于点O,连结C1O,
∵四边形ABCD是菱形,∴AC⊥BD,BC=CD
又∵∠BCC1=∠DCC1,C1C是公共边,∴△C1BC≌△C1DC,∴C1B=C1D
∵DO=OB,∴C1O⊥BD,但AC⊥BD,AC∩C1O=O
∴BD⊥平面AC1,又C1C![]() 平面AC1,∴C1C⊥BD.
平面AC1,∴C1C⊥BD.
(2)解:由(1)知AC⊥BD,C1O⊥BD,∴∠C1OC是二面角α—BD—β的平面角.
在△C1BC中,BC=2,C1C=![]() ,∠BCC1=60°,∴C1B2=22+(
,∠BCC1=60°,∴C1B2=22+(![]() )2-2×2×
)2-2×2×![]() ×cos60°=
×cos60°=![]() .
.
∵∠OCB=30°,∴OB=![]() ,BC=1,C1O=
,BC=1,C1O=![]() ,即C1O=C1C.
,即C1O=C1C.
作C1H⊥OC,垂足为H,则H是OC中点且OH=![]() ,∴cosC1OC=
,∴cosC1OC=![]()
(3)解:由(1)知BD⊥平面AC1,∵A1O![]() 平面AC1,∴BD⊥A1C,当
平面AC1,∴BD⊥A1C,当![]() =1时,平行六面体的六个面是全等的菱形,同理可证BC1⊥A1C,又∵BD∩BC1=B,∴A1C⊥平面C1BD.
=1时,平行六面体的六个面是全等的菱形,同理可证BC1⊥A1C,又∵BD∩BC1=B,∴A1C⊥平面C1BD.
空间的角
【复习要点】
空间角的计算步骤:一作、二证、三算
1.异面直线所成的角 范围:0°<θ≤90°
方法:①平移法;②补形法.
2.直线与平面所成的角 范围:0°≤θ≤90°
方法:关键是作垂线,找射影.
3.二面角
方法:①定义法;②三垂线定理及其逆定理;③垂面法.
注:二面角的计算也可利用射影面积公式S′=Scosθ来计算
【例题】
【例1】 如图,α—l—β为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.
(1)求证:MN分别与α、β所成角相等;
(2)求MN与β所成角.
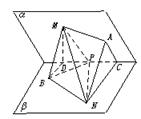
解:(1)证明:作NA⊥α于A,MB⊥β于B,连接AP、PB、BN、AM,再作AC⊥l于C,BD⊥l于D,连接NC、MD.
∵NA⊥α,MB⊥β,∴∠MPB、∠NPA分别是MP与β所成角及NP与α所成角,∠MNB,∠NMA分别是MN与β,α所成角,∴∠MPB=∠NPA.
在Rt△MPB与Rt△NPA中,PM=PN,∠MPB=∠NPA,∴△MPB≌△NPA,∴MB=NA.
在Rt△MNB与Rt△NMA中,MB=NA,MN是公共边,∴△MNB≌△NMA,∴∠MNB=∠NMA,即(1)结论成立.
(2)解:设∠MNB=θ,MN=![]() a,则PB=PN=a,MB=NA=
a,则PB=PN=a,MB=NA=![]() asinθ,NB=
asinθ,NB=![]() acosθ,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α—l—β的平面角,
acosθ,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α—l—β的平面角,
∴∠MDB=60°,同理∠NCA=60°,
∴BD=AC=![]() asinθ,CN=DM=
asinθ,CN=DM=![]() asinθ,
asinθ,
∵MB⊥β,MP⊥PN,∴BP⊥PN
∵∠BPN=90°,∠DPB=∠CNP,∴△BPD∽△PNC,∴![]()
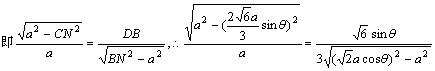
整理得,16sin4θ-16sin2θ+3=0
解得sin2θ=![]() ,sinθ=
,sinθ=![]() ,当sinθ=
,当sinθ=![]() 时,CN=
时,CN=![]() asinθ=
asinθ= ![]() a>PN不合理,舍去.
a>PN不合理,舍去.
∴sinθ=![]() ,∴MN与β所成角为30°.
,∴MN与β所成角为30°.
【例2】 在棱长为a的正方体ABCD—A′B′C′D′中,E、F分别是BC、A′D′的中点.
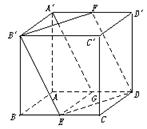
(1)求证:四边形B′EDF是菱形;
(2)求直线A′C与DE所成的角;
(3)求直线AD与平面B′EDF所成的角;
(4)求面B′EDF与面ABCD所成的角.
解:
(1)证明:如上图所示,由勾股定理,得B′E=ED=DF=FB′=![]() a,下证B′、E、D、F四点共面,取AD中点G,连结A′G、EG,由EG
a,下证B′、E、D、F四点共面,取AD中点G,连结A′G、EG,由EG![]() AB
AB![]() A′B′知,B′EGA′是平行四边形.
A′B′知,B′EGA′是平行四边形.
∴B′E∥A′G,又A′F
![]() DG,∴A′GDF为平行四边形.
DG,∴A′GDF为平行四边形.
∴A′G∥FD,∴B′、E、D、F四点共面
故四边形B′EDF是菱形.
(2)解:如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,
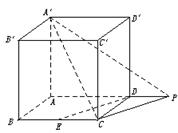
则∠A′CP(或补角)为异面直线A′C与DE所成的角.
在△A′CP中,易得A′C=![]() a,CP=DE=
a,CP=DE=![]() a,A′P=
a,A′P=![]() a
a
由余弦定理得cosA′CP=![]()
故A′C与DE所成角为arccos![]() .
.
(3)解:∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上.如下图所示.
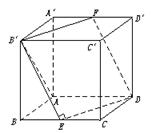
又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
故直线AD与平面B′EDF所成的角为∠ADB′
在Rt△B′AD中,AD=![]() a,AB′=
a,AB′=![]() a,B′D=
a,B′D=![]() a
a
则cosADB′=![]()
故AD与平面B′EDF所成的角是arccos![]() .
.
(4)解:如图,连结EF、B′D,交于O点,显然O为B′D的中点,从而O为正方形ABCD—A′B′C′D的中心.
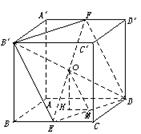
作OH⊥平面ABCD,则H为正方形ABCD的中心,
再作HM⊥DE,垂足为M,连结OM,则OM⊥DE,
故∠OMH为二面角B′—DE′—A的平面角.
在Rt△DOE中,OE=![]() a,OD=
a,OD=![]() a,斜边DE=
a,斜边DE=![]() a,
a,
则由面积关系得OM=![]() a
a
在Rt△OHM中,sinOMH=![]()
故面B′EDF与面ABCD所成的角为arcsin![]() .
.
【例3】 如下图,已知平行六面体ABCD—A1B1C1D1中,底面ABCD是边长为a的正方形,侧棱AA1长为b,且AA1与AB、AD的夹角都是120°.
求:(1)AC1的长;
(2)直线BD1与AC所成的角的余弦值.
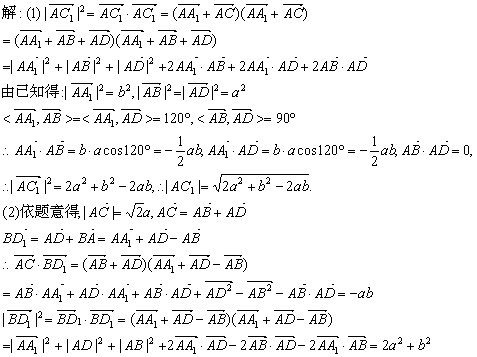
![]()
![]()
 ∴BD1与AC所成角的余弦值为
∴BD1与AC所成角的余弦值为![]() .
.
【例4】
长方体![]() 中,
中,![]() ,
,
![]() ,
,![]() 是侧棱
是侧棱![]() 中点.
中点.
(1)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)求二面角![]() 的大小;
的大小;
(3)求三棱锥![]() 的体积.
的体积.
解:(1)要求线面所成角,首先需要找到这个角,为此,我们应该先作出面![]() 的一条垂线.不难发现,
的一条垂线.不难发现,![]() 正为所求.
正为所求.
由长方体![]() 知:
知:![]() ,又
,又![]() ,所以,
,所以,![]() .
.
在矩形![]() 中,
中,![]() 为
为![]() 中点且
中点且![]() ,
,![]() ,所以,
,所以,![]() ,所以,
,所以,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.
所以,![]() 面
面![]() .
.
所以,![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角,为
所成的角,为![]() .
.
(2)要作出二面角的平面角,一般的思路是最好能找到其中一个面的一条垂线,则可利用三垂线定理(或逆定理)将其作出.
 注意到
注意到![]() ,所以,面
,所以,面![]()
![]() ,所以,只需在
,所以,只需在![]() 内过点
内过点![]() 作
作![]() 于F,则
于F,则![]() 面
面![]() .
.
过![]() 作
作![]() 于G,连EG,则
于G,连EG,则![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,
所以,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
所以,二面角![]() 的平面角的大小为
的平面角的大小为![]() .
.
(3)要求三棱锥![]() 的体积,注意到(2)中已经求出了点
的体积,注意到(2)中已经求出了点![]() 到平面
到平面![]() 的距离EF.所以,
的距离EF.所以,
![]() .
.
另一方面,也可以利用等积转化.
因为![]() ,所以,
,所以,![]()
![]() .所以,点A到平
.所以,点A到平![]() 的距离就等于点
的距离就等于点![]() 到平
到平![]() 的距离.所以,
的距离.所以,
![]() .
.
【例5】
如图,已知![]() 面
面![]() ,
,![]() 于D,
于D,![]() 。
。
(1)令![]() ,
,![]() ,试把
,试把![]() 表示为
表示为![]() 的函数,并求其最大值;
的函数,并求其最大值;
(2)在直线PA上是否存在一点Q,使得![]() ?
?
解:(1)为寻求![]() 与
与![]() 的关系,首先可以将
的关系,首先可以将![]() 转化为
转化为![]() 。
。
 ∵
∵ ![]() 面
面![]() ,
,![]() 于D,
于D,
∴ ![]() 。
。
∴![]() 。
。
∴ ![]()
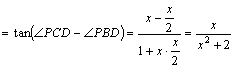 。
。
∵ ![]() 为
为![]() 在面
在面![]() 上的射影。
上的射影。
∴ ![]() ,即
,即![]() 。
。
∴ ![]()
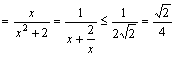 。
。
即![]() 的最大值为
的最大值为![]() ,等号当且仅当
,等号当且仅当![]() 时取得。
时取得。
(2)由正切函数的单调性可知:点Q的存在性等价于:是否存在点Q使得![]()
![]() 。
。
![]() 。
。
令![]()
![]()
![]() ,解得:
,解得:![]() ,与
,与![]() 交集非空。
交集非空。
∴ 满足条件的点Q存在。
【例6】
如图所示:正四棱锥![]() 中,侧棱
中,侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() 。(1)求侧面
。(1)求侧面![]() 与底面
与底面![]() 所成二面角的大小;
所成二面角的大小;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值;
(3)在侧面![]() 上寻找一点F,使得EF
上寻找一点F,使得EF![]() 侧面PBC。试确定点F的位置,并加以证明。
侧面PBC。试确定点F的位置,并加以证明。
 解:(1)连
解:(1)连![]() 交于点
交于点![]() ,连PO,
,连PO,
则PO⊥面ABCD,
∴ ∠PAO就是![]() 与底面
与底面![]() 所成的角,
所成的角,
∴ tan∠PAO=![]() 。
。
设AB=1,则PO=AO•tan∠PAO = ![]() 。
。
设F为AD中点,连FO、PO,则OF⊥AD,所以,PF⊥AD,所以,![]() 就是侧面
就是侧面![]() 与底面
与底面![]() 所成二面角的平面角。
所成二面角的平面角。
在Rt![]() 中,
中,![]() ,
,
∴ ![]() 。即面
。即面![]() 与底面
与底面![]() 所成二面角的大小为
所成二面角的大小为![]()
(2)由(1)的作法可知:O为BD中点,又因为E为PD中点,所以,![]()
![]()
![]() 。
。
∴![]() 就是异面直线PD与AE所成的角。
就是异面直线PD与AE所成的角。
 在Rt
在Rt![]() 中,
中,![]() 。
。
∴ ![]() 。
。
由![]() ,
,![]() 可知:
可知:![]() 面
面![]() 。
。
所以,![]() 。
。
在Rt![]() 中,
中,![]() 。
。
∴异面直线PD与AE所成的角为![]() 。
。
(3)对于这一类探索性的问题,作为一种探索,我们首先可以将条件放宽一些,即先找到面![]() 的一条垂线,然后再平移到点E即可。
的一条垂线,然后再平移到点E即可。
为了达到上述目的,我们可以从考虑面面垂直入手,不难发现:![]() 。
。
延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 。设
。设![]() 为
为![]() 中点,连接
中点,连接![]() 。
。
∵ 四棱锥![]() 为正四棱锥且
为正四棱锥且![]() 为
为![]() 中点,所以,
中点,所以,![]() 为
为![]() 中点,
中点,
∴ ![]() ,
,![]() 。
。
∴ ![]() 。∴ 面
。∴ 面![]() ⊥
⊥![]() 。
。
∵ ![]() ,
,![]() ,∴
,∴ ![]() 为正三角形。
为正三角形。
∴ ![]() ,∴
,∴ ![]() 。
。
取AF中点为K,连EK,则由![]() 及
及![]() 得四边形
得四边形![]() 为平行四边形,所以,
为平行四边形,所以,![]() 。
。
∴![]() 。
。
【例7】
 RtΔABC中,AC=BC=1,∠BCA=90°,现将ΔABC沿着平面ABC的法向量平移到ΔA1B1C1位置,已知AA1=2,分别取A1B1、A1A的中点P、Q,
RtΔABC中,AC=BC=1,∠BCA=90°,现将ΔABC沿着平面ABC的法向量平移到ΔA1B1C1位置,已知AA1=2,分别取A1B1、A1A的中点P、Q,
(1)求![]() 的长;
的长;
(2)求证:AB1⊥C1P;
(3)求cos<![]() ,
,![]() >,cos<
>,cos<![]() ,
,![]() >,
>,
并比较<![]() ,
,![]() >与<
>与<![]() ,
,![]() >的大小.
>的大小.
 解:以C为原点,建立如图空间直角坐标系O-xyz,
解:以C为原点,建立如图空间直角坐标系O-xyz,
(1)∵![]() =(1,-1,1),
=(1,-1,1),
∴ ![]() =
=![]()
(2)∵![]() =(-1,1,3),
=(-1,1,3),![]() =(
=(![]() ,
,![]() ,0)
,0)
∴![]() ·
·![]() =(-1)×
=(-1)×![]() +1×
+1×![]() +2×0=0,
+2×0=0,
∴![]() ⊥
⊥![]() ,
,
即![]() ⊥
⊥![]()
(3)![]() =(0,1,2),
=(0,1,2),![]() =(1,-1,2),
=(1,-1,2),
cos<![]() ,
,![]() >=
>=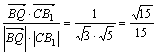 ,
,
同理,cos<![]() ,
,![]() >=
>=![]()
 ∵0<
∵0<![]() <
<![]() <1,<
<1,<![]() ,
,![]() >,<
>,<![]() ,
,![]() >∈(0,
>∈(0,![]() )
)
∴<![]() ,
,![]() >><
>><![]() ,
,![]() >
>
【例8】
如图:直三棱柱![]() 中,
中,![]() ,
,![]() 。
。![]() 为
为![]() 的中点,
的中点,![]() 点在
点在![]() 上且
上且![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
解:1)证:依题意知![]() ,
,![]() 且
且
![]() 为
为![]() 的中点,则
的中点,则
![]() 也为
也为![]() 中点
中点
∴![]()
又∵三棱柱![]() 为直三棱柱
为直三棱柱
∴![]()
又 ![]() 且
且 ![]() 、
、![]()
故 ![]() .
.
2)解:由1)知![]() ,在
,在![]() 中过
中过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
连![]() ,由三垂线定理有
,由三垂线定理有![]() 为所求二面角得平面角
为所求二面角得平面角
易知![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]()
故![]()
![]()
在![]() 中
中 ![]()
故所求二面角的大小为![]() .
.
【例9】
 如图,在多面体
如图,在多面体![]() 中,
中,![]() 面
面![]() ,
,![]() ∥
∥![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求证:![]() 面
面![]() ;
;
(2)求多面体![]() 的体积;
的体积;
(3)求面![]() 与面
与面![]() 所成的二面角的余弦值.
所成的二面角的余弦值.
解:(1)取![]() 中点
中点![]() ,连
,连![]() ,
,![]() .
.
∵![]() 面
面![]() ,
,![]() ∥
∥![]() ,∴
,∴![]() 面
面![]() ,
,
又![]() 面
面![]() ,∴
,∴![]() ,又
,又![]() ,
,
![]() 是
是![]() 中点,
中点,
∴![]() ,∴
,∴![]()
![]() 平面
平面![]() ,∵
,∵![]() 是
是![]() 的中点且
的中点且![]() ,
,
∴![]() ∥
∥![]() 且
且![]() ,∴
,∴![]() ∥
∥![]() ,
,
又![]() ,∴
,∴![]() ,故四边形
,故四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ∥
∥![]() ,
,
∴![]() 面
面![]() .
.
(2)设![]() 中点为
中点为![]() ,则由
,则由![]() 可得
可得![]() 且
且![]() ,
,
又∵![]() ∥
∥![]() ,∴
,∴![]() 与
与![]() 共面,又
共面,又![]() 面
面![]() ,故平面
,故平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 为四棱锥
为四棱锥![]() 的高.
的高.
故![]() ·
·![]() .
.
(3)过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,由三垂线定理的逆定理得
,由三垂线定理的逆定理得![]() ,
,
 ∴
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
易知![]() ,
,![]() ,
,![]() ,
,
由![]() ,
,
可得![]() ,在
,在![]() 中,
中, ![]() ,故
,故![]() ,
,
∴面![]() 与面
与面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.
【空间的角练习】
一、选择题
1.在正方体ABCD—A1B1C1D1中,M为DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设△ABC和△DBC所在两平面互相垂直,且AB=BC=BD=a,∠CBA=
∠CBD=120°,则AD与平面BCD所成的角为( )
A.30° B.45° C.60° D.75°
二、填空题
3.已知∠AOB=90°,过O点引∠AOB所在平面的斜线OC,与OA、OB分别成45°、60°,则以OC为棱的二面角A—OC—B的余弦值等于_________.
4.正三棱锥的一个侧面的面积与底面积之比为2∶3,则这个三棱锥的侧面和底面所成二面角的度数为_________.
三、解答题
5,已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小;
(3)求证:二面角B—PC—D为直二面角.
6.设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=
∠DBC=120°
求:(1)直线AD与平面BCD所成角的大小;
(2)异面直线AD与BC所成的角;
(3)二面角A—BD—C的大小.
7.一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.
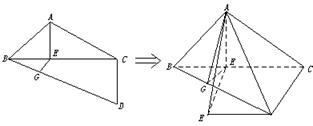
(1)求证:平面ABD⊥平面ACD;
(2)求AD与BC所成的角;
(3)求二面角A—BD—C的大小.
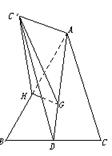
8.设D是△ABC的BC边上一点,把△ACD沿AD折起,使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.
(1)求证:直线C′D与平面ABD和平面AHC′所成的两个角之和不可能超过90°;
(2)若∠BAC=90°,二面角C′—AD—H为60°,求∠BAD的正切值.
参考答案
一、1.解析:(特殊位置法)将P点取为A1,作OE⊥AD于E,连结A1E,则A1E为OA1的射影,又AM⊥A1E,∴AM⊥OA1,即AM与OP成90°角.
答案:D
2.解析:作AO⊥CB的延长线,连OD,则OD即为AD在平面BCD上的射影,
∵AO=OD=![]() a,∴∠ADO=45°.
a,∴∠ADO=45°.
答案:B
二、3.解析:在OC上取一点C,使OC=1,过C分别作CA⊥OC交OA于A,CB⊥OC交OB于B,则AC=1,,OA=![]() ,BC=
,BC=![]() ,OB=2,Rt△AOB中,AB2=6,△ABC中,由余弦定理,得cosACB=-
,OB=2,Rt△AOB中,AB2=6,△ABC中,由余弦定理,得cosACB=-![]() .
.
答案:-![]()
4.解析:设一个侧面面积为S1,底面面积为S,则这个侧面在底面上射影的面积为![]() ,由题设得
,由题设得![]() ,设侧面与底面所成二面角为θ,则cosθ=
,设侧面与底面所成二面角为θ,则cosθ=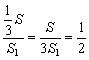 ,∴θ=60°.
,∴θ=60°.
答案:60°
三、5.(1)解:因为PA⊥平面AC,AB⊥BC,∴PB⊥BC,即∠PBC=90°,由勾股定理得PB=![]() .
.
∴PC=![]() .
.
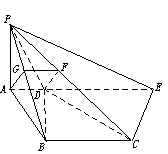
(2)解:如图,过点C作CE∥BD交AD的延长线于E,连结PE,则PC与BD所成的角为∠PCE或它的补角.
∵CE=BD=![]() ,且PE=
,且PE=![]()
∴由余弦定理得cosPCE=![]()
∴PC与BD所成角的余弦值为![]() .
.
(3)证明:设PB、PC中点分别为G、F,连结FG、AG、DF,则GF∥BC∥AD,且GF=![]() BC=1=AD,从而四边形ADFG为平行四边形,
BC=1=AD,从而四边形ADFG为平行四边形,
又AD⊥平面PAB,∴AD⊥AG,即ADFG为矩形,DF⊥FG.
在△PCD中,PD=![]() ,CD=
,CD=![]() ,F为BC中点,∴DF⊥PC
,F为BC中点,∴DF⊥PC
从而DF⊥平面PBC,故平面PDC⊥平面PBC,即二面角B—PC—D为直二面角.
6.解:(1)如图,在平面ABC内,过A作AH⊥BC,垂足为H,则AH⊥平面DBC,
∴∠ADH即为直线AD与平面BCD所成的角.由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,
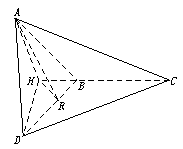
∴∠ADH=45°
(2)∵BC⊥DH,且DH为AD在平面BCD上的射影,
∴BC⊥AD,故AD与BC所成的角为90°.
(3)过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A—BD—C的平面角的补角.设BC=a,则由题设知,AH=DH=![]() ,在△HDB中,HR=
,在△HDB中,HR=![]() a,∴tanARH=
a,∴tanARH=![]() =2
=2
故二面角A—BD—C大小为π-arctan2.
7.(1)证明:取BC中点E,连结AE,∵AB=AC,∴AE⊥BC
∵平面ABC⊥平面BCD,∴AE⊥平面BCD,
∵BC⊥CD,由三垂线定理知AB⊥CD.
又∵AB⊥AC,∴AB⊥平面BCD,∵AB![]() 平面ABD.
平面ABD.
∴平面ABD⊥平面ACD.
(2)解:在面BCD内,过D作DF∥BC,过E作EF⊥DF,交DF于F,由三垂线定理知AF⊥DF,∠ADF为AD与BC所成的角.
设AB=m,则BC=![]() m,CE=DF=
m,CE=DF=![]() m,CD=EF=
m,CD=EF=![]() m
m
![]()
即AD与BC所成的角为arctan![]()
(3)解:∵AE⊥面BCD,过E作EG⊥BD于G,连结AG,由三垂线定理知AG⊥BD,
∴∠AGE为二面角A—BD—C的平面角
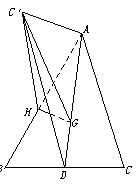
∵∠EBG=30°,BE=![]() m,∴EG=
m,∴EG=![]() m
m
又AE=![]() m,∴tanAGE=
m,∴tanAGE=![]() =2,∴∠AGE=arctan2.
=2,∴∠AGE=arctan2.
即二面角A—BD—C的大小为arctan2.
8.(1)证明:连结DH,∵C′H⊥平面ABD,∴∠C′DH为C′D与平面ABD所成的角且平面C′HA⊥平面ABD,过D作DE⊥AB,垂足为E,则DE⊥平面C′HA.
故∠DC′E为C′D与平面C′HA所成的角
∵sinDC′E=![]() ≤
≤![]() =sinDC′H
=sinDC′H
∴∠DC′E≤∠DC′H,
∴∠DC′E+∠C′DE≤∠DC′H+∠C′DE=90°
(2)解:作HG⊥AD,垂足为G,连结C′G,
则C′G⊥AD,故∠C′GH是二面角C′—AD—H的平面角
即∠C′GH=60°,计算得tanBAD=![]() .
.
【练习2】
1.下列命题中,正确的是( )
A.如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直
B.如果一个平面内两条直线都平行于另一平面,那么这两个平面平行。
C.如果两条直线都平行于同一平面,那么这两条直线平行
D.如果一条直线上有两个点到一个平面的距离相等,那么这条直线和这个平面平行。
2.下面的四个命题:( )
(1)若直线a//平面a,则平面a内的任何直线都与直线a平行
(2)若直线a^平面a,则平面a内的任何直线都与直线a垂直
(3)若平面a//平面b,则平面b内的任何直线都与平面a平行
(4)若平面a^平面b,则平面b内的任何直线都与平面a垂直;
其中正确的命题的个数是:( )
A.0 B.1 C.2 D.3
3.已知平面a与平面b相交,直线m^平面a,则:( )
A.b内不一定存在直线与m平行,但必存在直线与m垂直
B.b内必存在直线与m平行,且必存在直线与m垂直
C.b内不一定存在直线与m平行,不一定存在直线与m垂直
D.b内必存在直线与m平行,不一定存在直线与m垂直
4.已知a、b、g表示不同的平面,a、b表示不同的直线,下列命题中正确的是:( )
A.如果a//a,a^b,那么a^b B.如果a^b,b^g,那么a^g
C.如果a^a,a^b,那么a//b D.如果a//b,b//a,那么a//a
5.设a,b表示平面,L表示不在a内也不在b内的直线,存在下列三个事实:(1)L^a;(2)a^b;(3)L//b,若以其中两个作为条件,另一个作为结论,则可以构成三个命题,这三个命题中,正确命题的个数是:( )
A.0 B.1 C.2 D.3
6.设a、b、c是不同的直线,α,b是不同的平面,下列三个命题:
(1)若a//b,则a与c所成的角和b与c所成的角相等
(2)若a//b,则a与α所成的解和b与α所成的角相等
(3)若α//b,则a与α所成的角和a与b所成的角相等
其中,正确命题的个数是:( )
A.0 B.1 C.2 D.3
7.已知m、n是直线,a、b、g是平面,给出下列命题
(1)若a^g,b^g则a//b (2)若u^a,u^b,则a//b
(3)若a内不共线的三点到平面b的距离都相等,则a//b
(4)若n Ì a,m Ì a,且n//b,m//b,则a//b;
(5)若m,n为异面直线,且n Ì a,n//b,m Ì b,m//a,则a//b
其中正确的两个命题是:( )
A.(1)与(2) B.(3)与(4) C.(2)与(5)
D.(2)与(3)
8.已知直二面角a—L—b,且a Ì a,b Ì b, 且a,b与L均不垂直,则下列命题正确的是;( )
A.a和b不可能垂直,也不可能平行 B.a和b不可能垂直,但可能平行
C.a和b可能垂直,但不可能平行 D.a和b可能垂直,也可能平行
9.已知直线l1,l2与平面a,有下面四个命题:
(1)若l1//a,l1//l2,则l2//a (2)若l1Ìa,l2Ça=A,,则l1,l2异面
(3)若l1^a,l2^a,,则l1//l2 (4)若l1^l2,l1^a,则l2//a
其中真命题有:( )
A.0个 B.1个 C.2个 D.3个
10.正方体ABCD-A1B1C1D1中,直线BD1与直线AC所成的角是:( )
A.30° b.45° c.60° d.90°
11.已知PA垂直于正方形ABCD所在的平面于A点,边PB、PC、PD、AC、BD,则互相垂直的平面有:( )
A.5对 B.6对 C.7对 D.8对
12.空间有6个点,任意四点都不共面,过其中任意两点均有一条直线,则成为异面直线的对数为( )
A.15 B.30 C.45 D.60
13.下面命题中
(1)两条异面直线a,b中,a//平面a,则b//a
(2)若平面a//平面b,aÌ a,则a//b
(3)若aÇb=a,直线a^b,若使b^a,则只须bÌb,且a^b
(4)直线a,bÌa,直线lÇa=A且l^a,b^a,则b与l在a内的射影垂直( )
A.(1)(2) B.(2)(3) C.(1)(2)(3) D.(2)(3)(4)
14.直线L与△ABC三边均不相交,L上有四点D、E、F、G且这四点均不在直线AB、AC、BC上,则A、B、C、D、E、F、G七个点可确定三角形的个数是;( )
A.35 B.33 C.31 D.29
15.设a、b表示直线,a、b、g表示平面,给出下列命题:
(1)若a^g,且b^g,则a//b
(2)若a内有不共线的三个点到b的距离相等,则a//b
(3)若a Ì a,b Ì b,且a//b,b//a,则a//b
(4)若a,b是异面直线,aÌa,bÌb,且a//b,b//a,则a//b
其中正确命题的序号是 。(注,把你认为正确的命题的序号都填上)
16.已知a,b,c是三条不重合的直线,a、b、g是三个不重合的平面,给出下面六个命题:
(1)若a//c,b//c,则a//b (2)若a//g,b//g,则a//b
(3)若a//c,b//c,,则a//b (4)若a//g,b//g,则a//b
(5)若a//c,a//c,则a//a (6)若a//g,a//g,则a//a
其中正确的命题的序号是: 。
17.已知m,l是异面直线,给出下列命题
(1)一定存在平面a过m且与l平行 (2)一定存在平面a与m、l都垂直
(3)一定存在平面a过m且与l垂直 (4)一定存在平面a与m、l的距离相等
其中不正确的命题的序号
18.设a、b表示直线,a、b、g表示平面,给出下列命题:
(1)若a^g,且b^g,则a//b
(2)若a内有不共线的三个点到b的距离相等,则a//b
(3)若a Ì a,b Ì b,且a//b,b//a,则a//b
(4)若a,b是异面直线,aÌa,bÌb,且a//b,b//a,则a//b
其中正确命题的序号是 。(注,把你认为正确的命题的序号都填上)
19.已知a,b,c是三条不重合的直线,a、b、g是三个不重合的平面,给出下面六个命题:
(1)若a//c,b//c,则a//b (2)若a//g,b//g,则a//b
(3)若a//c,b//c,,则a//b (4)若a//g,b//g,则a//b
(5)若a//c,a//c,则a//a (6)若a//g,a//g,则a//a
其中正确的命题的序号是: 。
20.已知m,l是异面直线,给出下列命题
(1)一定存在平面a过m且与l平行 (2)一定存在平面a与m、l都垂直
(3)一定存在平面a过m且与l垂直 (4)一定存在平面a与m、l的距离相等
其中不正确的命题的序号 。
21.![]() 是不重合的2个平面,在
是不重合的2个平面,在![]() 上任取5个点,在
上任取5个点,在![]() 上任取4个点,由这些点所确定的平面的个数最多是(
C )
上任取4个点,由这些点所确定的平面的个数最多是(
C )
A.42个 B.70个 C.72个 D.84个
22.若平面![]() ⊥平面
⊥平面![]() ,又直线
,又直线![]() ,直线
,直线![]() ,且
,且![]() ,则( D
)
,则( D
)
A.![]() B.
B.![]() C.
C.![]() 且
且![]() D.
D.![]() 或
或![]()
23.已知二面角![]() 是直二面角,P为棱AB上一点,PQ、PR分别在平面
是直二面角,P为棱AB上一点,PQ、PR分别在平面![]() 、
、![]() 内,且
内,且![]() ,则
,则![]() 为( B )
为( B )
A.45° B.60° C.120° D.150°
24.正方体的棱长为![]() ,由它的互不相邻的四个顶点连线所构成的四面体的体积是
,由它的互不相邻的四个顶点连线所构成的四面体的体积是
( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
26.平行六面体的棱长均为4,由同一顶点出发的三条棱上分别取![]() 1,
1,![]()
![]() ,则三棱锥
,则三棱锥![]() 的体积与平行六面体的体积之比是( A )
的体积与平行六面体的体积之比是( A )
A.1∶64 B.2∶7 C.7∶19 D.3∶16
27.在正方体![]() 中,二面角
中,二面角![]() 的度数是( C
)
的度数是( C
)
A.45° B.60° C.120° D.135°
|
|
28.正方形![]() 被对角线BD和以A为圆心,AB为半径的圆弧
被对角线BD和以A为圆心,AB为半径的圆弧![]() 分成三部分,绕AD旋转,所得旋转体的体积
分成三部分,绕AD旋转,所得旋转体的体积![]() 之比是( C
)
之比是( C
)
A.2∶1∶1 B.1∶2∶1
C.1∶1∶1 D.2∶2∶1
29.在四棱锥的四个侧面中,直角三角形最多可有( D )
A.1个 B.2个 C.3个 D.4个
空间的角
【复习要点】
空间角的计算步骤:一作、二证、三算
1.异面直线所成的角 范围:0°<θ≤90°
方法:①平移法;②补形法.
2.直线与平面所成的角 范围:0°≤θ≤90°
方法:关键是作垂线,找射影.
3.二面角
方法:①定义法;②三垂线定理及其逆定理;③垂面法.
注:二面角的计算也可利用射影面积公式S′=Scosθ来计算
【例题】
【例10】 如图,α—l—β为60°的二面角,等腰直角三角形MPN的直角顶点P在l上,M∈α,N∈β,且MP与β所成的角等于NP与α所成的角.
(1)求证:MN分别与α、β所成角相等;
(2)求MN与β所成角.

解:(1)证明:作NA⊥α于A,MB⊥β于B,连接AP、PB、BN、AM,再作AC⊥l于C,BD⊥l于D,连接NC、MD.
∵NA⊥α,MB⊥β,∴∠MPB、∠NPA分别是MP与β所成角及NP与α所成角,∠MNB,∠NMA分别是MN与β,α所成角,∴∠MPB=∠NPA.
在Rt△MPB与Rt△NPA中,PM=PN,∠MPB=∠NPA,∴△MPB≌△NPA,∴MB=NA.
在Rt△MNB与Rt△NMA中,MB=NA,MN是公共边,∴△MNB≌△NMA,∴∠MNB=∠NMA,即(1)结论成立.
(2)解:设∠MNB=θ,MN=![]() a,则PB=PN=a,MB=NA=
a,则PB=PN=a,MB=NA=![]() asinθ,NB=
asinθ,NB=![]() acosθ,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α—l—β的平面角,
acosθ,∵MB⊥β,BD⊥l,∴MD⊥l,∴∠MDB是二面角α—l—β的平面角,
∴∠MDB=60°,同理∠NCA=60°,
∴BD=AC=![]() asinθ,CN=DM=
asinθ,CN=DM=![]() asinθ,
asinθ,
∵MB⊥β,MP⊥PN,∴BP⊥PN
∵∠BPN=90°,∠DPB=∠CNP,∴△BPD∽△PNC,∴![]()
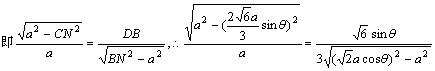
整理得,16sin4θ-16sin2θ+3=0
解得sin2θ=![]() ,sinθ=
,sinθ=![]() ,当sinθ=
,当sinθ=![]() 时,CN=
时,CN=![]() asinθ=
asinθ= ![]() a>PN不合理,舍去.
a>PN不合理,舍去.
∴sinθ=![]() ,∴MN与β所成角为30°.
,∴MN与β所成角为30°.
【例11】 在棱长为a的正方体ABCD—A′B′C′D′中,E、F分别是BC、A′D′的中点.
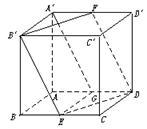
(1)求证:四边形B′EDF是菱形;
(2)求直线A′C与DE所成的角;
(3)求直线AD与平面B′EDF所成的角;
(4)求面B′EDF与面ABCD所成的角.
解:
(1)证明:如上图所示,由勾股定理,得B′E=ED=DF=FB′=![]() a,下证B′、E、D、F四点共面,取AD中点G,连结A′G、EG,由EG
a,下证B′、E、D、F四点共面,取AD中点G,连结A′G、EG,由EG![]() AB
AB![]() A′B′知,B′EGA′是平行四边形.
A′B′知,B′EGA′是平行四边形.
∴B′E∥A′G,又A′F
![]() DG,∴A′GDF为平行四边形.
DG,∴A′GDF为平行四边形.
∴A′G∥FD,∴B′、E、D、F四点共面
故四边形B′EDF是菱形.
(2)解:如图所示,在平面ABCD内,过C作CP∥DE,交直线AD于P,
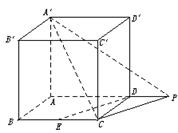
则∠A′CP(或补角)为异面直线A′C与DE所成的角.
在△A′CP中,易得A′C=![]() a,CP=DE=
a,CP=DE=![]() a,A′P=
a,A′P=![]() a
a
由余弦定理得cosA′CP=![]()
故A′C与DE所成角为arccos![]() .
.
(3)解:∵∠ADE=∠ADF,∴AD在平面B′EDF内的射影在∠EDF的平分线上.如下图所示.
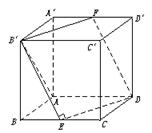
又∵B′EDF为菱形,∴DB′为∠EDF的平分线,
故直线AD与平面B′EDF所成的角为∠ADB′
在Rt△B′AD中,AD=![]() a,AB′=
a,AB′=![]() a,B′D=
a,B′D=![]() a
a
则cosADB′=![]()
故AD与平面B′EDF所成的角是arccos![]() .
.
(4)解:如图,连结EF、B′D,交于O点,显然O为B′D的中点,从而O为正方形ABCD—A′B′C′D的中心.
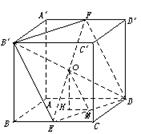
作OH⊥平面ABCD,则H为正方形ABCD的中心,
再作HM⊥DE,垂足为M,连结OM,则OM⊥DE,
故∠OMH为二面角B′—DE′—A的平面角.
在Rt△DOE中,OE=![]() a,OD=
a,OD=![]() a,斜边DE=
a,斜边DE=![]() a,
a,
则由面积关系得OM=![]() a
a
在Rt△OHM中,sinOMH=![]()
故面B′EDF与面ABCD所成的角为arcsin![]() .
.
【例12】 如下图,已知平行六面体ABCD—A1B1C1D1中,底面ABCD是边长为a的正方形,侧棱AA1长为b,且AA1与AB、AD的夹角都是120°.

求:(1)AC1的长;
(2)直线BD1与AC所成的角的余弦值.
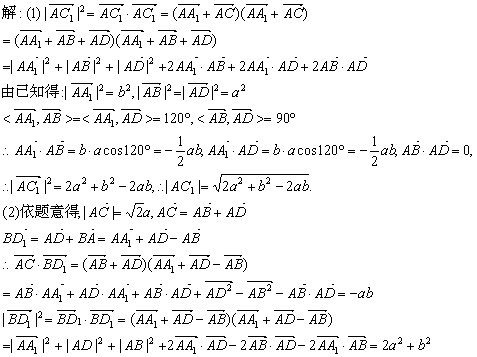
![]()
![]()
 ∴BD1与AC所成角的余弦值为
∴BD1与AC所成角的余弦值为![]() .
.
【例13】
长方体![]() 中,
中,![]() ,
,
![]() ,
,![]() 是侧棱
是侧棱![]() 中点.
中点.
(1)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(2)求二面角![]() 的大小;
的大小;
(3)求三棱锥![]() 的体积.
的体积.
解:(1)要求线面所成角,首先需要找到这个角,为此,我们应该先作出面![]() 的一条垂线.不难发现,
的一条垂线.不难发现,![]() 正为所求.
正为所求.
由长方体![]() 知:
知:![]() ,又
,又![]() ,所以,
,所以,![]() .
.
在矩形![]() 中,
中,![]() 为
为![]() 中点且
中点且![]() ,
,![]() ,所以,
,所以,![]() ,所以,
,所以,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.
所以,![]() 面
面![]() .
.
所以,![]() 就是直线
就是直线![]() 与平面
与平面![]() 所成的角,为
所成的角,为![]() .
.
(2)要作出二面角的平面角,一般的思路是最好能找到其中一个面的一条垂线,则可利用三垂线定理(或逆定理)将其作出.
 注意到
注意到![]() ,所以,面
,所以,面![]()
![]() ,所以,只需在
,所以,只需在![]() 内过点
内过点![]() 作
作![]() 于F,则
于F,则![]() 面
面![]() .
.
过![]() 作
作![]() 于G,连EG,则
于G,连EG,则![]() 就是二面角
就是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,
所以,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
所以,二面角![]() 的平面角的大小为
的平面角的大小为![]() .
.
(3)要求三棱锥![]() 的体积,注意到(2)中已经求出了点
的体积,注意到(2)中已经求出了点![]() 到平面
到平面![]() 的距离EF.所以,
的距离EF.所以,
![]() .
.
另一方面,也可以利用等积转化.
因为![]() ,所以,
,所以,![]()
![]() .所以,点A到平
.所以,点A到平![]() 的距离就等于点
的距离就等于点![]() 到平
到平![]() 的距离.所以,
的距离.所以,
![]() .
.
【例14】
如图,已知![]() 面
面![]() ,
,![]() 于D,
于D,![]() 。
。
(1)令![]() ,
,![]() ,试把
,试把![]() 表示为
表示为![]() 的函数,并求其最大值;
的函数,并求其最大值;
(2)在直线PA上是否存在一点Q,使得![]() ?
?
解:(1)为寻求![]() 与
与![]() 的关系,首先可以将
的关系,首先可以将![]() 转化为
转化为![]() 。
。
 ∵
∵ ![]() 面
面![]() ,
,![]() 于D,
于D,
∴ ![]() 。
。
∴![]() 。
。
∴ ![]()
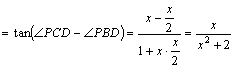 。
。
∵ ![]() 为
为![]() 在面
在面![]() 上的射影。
上的射影。
∴ ![]() ,即
,即![]() 。
。
∴ ![]()
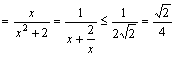 。
。
即![]() 的最大值为
的最大值为![]() ,等号当且仅当
,等号当且仅当![]() 时取得。
时取得。
(2)由正切函数的单调性可知:点Q的存在性等价于:是否存在点Q使得![]()
![]() 。
。
![]() 。
。
令![]()
![]()
![]() ,解得:
,解得:![]() ,与
,与![]() 交集非空。
交集非空。
∴ 满足条件的点Q存在。
【例15】
如图所示:正四棱锥![]() 中,侧棱
中,侧棱![]() 与底面
与底面![]() 所成角的正切值为
所成角的正切值为![]() 。(1)求侧面
。(1)求侧面![]() 与底面
与底面![]() 所成二面角的大小;
所成二面角的大小;
(2)若E是PB中点,求异面直线PD与AE所成角的正切值;
(3)在侧面![]() 上寻找一点F,使得EF
上寻找一点F,使得EF![]() 侧面PBC。试确定点F的位置,并加以证明。
侧面PBC。试确定点F的位置,并加以证明。
 解:(1)连
解:(1)连![]() 交于点
交于点![]() ,连PO,
,连PO,
则PO⊥面ABCD,
∴ ∠PAO就是![]() 与底面
与底面![]() 所成的角,
所成的角,
∴ tan∠PAO=![]() 。
。
设AB=1,则PO=AO•tan∠PAO = ![]() 。
。
设F为AD中点,连FO、PO,则OF⊥AD,所以,PF⊥AD,所以,![]() 就是侧面
就是侧面![]() 与底面
与底面![]() 所成二面角的平面角。
所成二面角的平面角。
在Rt![]() 中,
中,![]() ,
,
∴ ![]() 。即面
。即面![]() 与底面
与底面![]() 所成二面角的大小为
所成二面角的大小为![]()
(2)由(1)的作法可知:O为BD中点,又因为E为PD中点,所以,![]()
![]()
![]() 。
。
∴![]() 就是异面直线PD与AE所成的角。
就是异面直线PD与AE所成的角。
 在Rt
在Rt![]() 中,
中,![]() 。
。
∴ ![]() 。
。
由![]() ,
,![]() 可知:
可知:![]() 面
面![]() 。
。
所以,![]() 。
。
在Rt![]() 中,
中,![]() 。
。
∴异面直线PD与AE所成的角为![]() 。
。
(3)对于这一类探索性的问题,作为一种探索,我们首先可以将条件放宽一些,即先找到面![]() 的一条垂线,然后再平移到点E即可。
的一条垂线,然后再平移到点E即可。
为了达到上述目的,我们可以从考虑面面垂直入手,不难发现:![]() 。
。
延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 。设
。设![]() 为
为![]() 中点,连接
中点,连接![]() 。
。
∵ 四棱锥![]() 为正四棱锥且
为正四棱锥且![]() 为
为![]() 中点,所以,
中点,所以,![]() 为
为![]() 中点,
中点,
∴ ![]() ,
,![]() 。
。
∴ ![]() 。∴ 面
。∴ 面![]() ⊥
⊥![]() 。
。
∵ ![]() ,
,![]() ,∴
,∴ ![]() 为正三角形。
为正三角形。
∴ ![]() ,∴
,∴ ![]() 。
。
取AF中点为K,连EK,则由![]() 及
及![]() 得四边形
得四边形![]() 为平行四边形,所以,
为平行四边形,所以,![]() 。
。
∴![]() 。
。
【例16】
 RtΔABC中,AC=BC=1,∠BCA=90°,现将ΔABC沿着平面ABC的法向量平移到ΔA1B1C1位置,已知AA1=2,分别取A1B1、A1A的中点P、Q,
RtΔABC中,AC=BC=1,∠BCA=90°,现将ΔABC沿着平面ABC的法向量平移到ΔA1B1C1位置,已知AA1=2,分别取A1B1、A1A的中点P、Q,
(1)求![]() 的长;
的长;
(2)求证:AB1⊥C1P;
(3)求cos<![]() ,
,![]() >,cos<
>,cos<![]() ,
,![]() >,
>,
并比较<![]() ,
,![]() >与<
>与<![]() ,
,![]() >的大小.
>的大小.
 解:以C为原点,建立如图空间直角坐标系O-xyz,
解:以C为原点,建立如图空间直角坐标系O-xyz,
(1)∵![]() =(1,-1,1),
=(1,-1,1),
∴ ![]() =
=![]()
(2)∵![]() =(-1,1,3),
=(-1,1,3),![]() =(
=(![]() ,
,![]() ,0)
,0)
∴![]() ·
·![]() =(-1)×
=(-1)×![]() +1×
+1×![]() +2×0=0,
+2×0=0,
∴![]() ⊥
⊥![]() ,
,
即![]() ⊥
⊥![]()
(3)![]() =(0,1,2),
=(0,1,2),![]() =(1,-1,2),
=(1,-1,2),
cos<![]() ,
,![]() >=
>=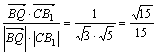 ,
,
同理,cos<![]() ,
,![]() >=
>=![]()
 ∵0<
∵0<![]() <
<![]() <1,<
<1,<![]() ,
,![]() >,<
>,<![]() ,
,![]() >∈(0,
>∈(0,![]() )
)
∴<![]() ,
,![]() >><
>><![]() ,
,![]() >
>
【例17】
如图:直三棱柱![]() 中,
中,![]() ,
,![]() 。
。![]() 为
为![]() 的中点,
的中点,![]() 点在
点在![]() 上且
上且![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
解:1)证:依题意知![]() ,
,![]() 且
且
![]() 为
为![]() 的中点,则
的中点,则
![]() 也为
也为![]() 中点
中点
∴![]()
又∵三棱柱![]() 为直三棱柱
为直三棱柱
∴![]()
又 ![]() 且
且 ![]() 、
、![]()
故 ![]() .
.
2)解:由1)知![]() ,在
,在![]() 中过
中过![]() 作
作![]() 交
交![]() 于
于![]() ,
,
连![]() ,由三垂线定理有
,由三垂线定理有![]() 为所求二面角得平面角
为所求二面角得平面角
易知![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]()
故![]()
![]()
在![]() 中
中 ![]()
故所求二面角的大小为![]() .
.
【例18】
 如图,在多面体
如图,在多面体![]() 中,
中,![]() 面
面![]() ,
,![]() ∥
∥![]() ,且
,且![]()
![]() ,
,![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求证:![]() 面
面![]() ;
;
(2)求多面体![]() 的体积;
的体积;
(3)求面![]() 与面
与面![]() 所成的二面角的余弦值.
所成的二面角的余弦值.
解:(1)取![]() 中点
中点![]() ,连
,连![]() ,
,![]() .
.
∵![]() 面
面![]() ,
,![]() ∥
∥![]() ,∴
,∴![]() 面
面![]() ,
,
又![]() 面
面![]() ,∴
,∴![]() ,又
,又![]() ,
,
![]() 是
是![]() 中点,
中点,
∴![]() ,∴
,∴![]()
![]() 平面
平面![]() ,∵
,∵![]() 是
是![]() 的中点且
的中点且![]() ,
,
∴![]() ∥
∥![]() 且
且![]() ,∴
,∴![]() ∥
∥![]() ,
,
又![]() ,∴
,∴![]() ,故四边形
,故四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ∥
∥![]() ,
,
∴![]() 面
面![]() .
.
(2)设![]() 中点为
中点为![]() ,则由
,则由![]() 可得
可得![]() 且
且![]() ,
,
又∵![]() ∥
∥![]() ,∴
,∴![]() 与
与![]() 共面,又
共面,又![]() 面
面![]() ,故平面
,故平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 为四棱锥
为四棱锥![]() 的高.
的高.
故![]() ·
·![]() .
.
(3)过![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,由三垂线定理的逆定理得
,由三垂线定理的逆定理得![]() ,
,
 ∴
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
易知![]() ,
,![]() ,
,![]() ,
,
由![]() ,
,
可得![]() ,在
,在![]() 中,
中, ![]() ,故
,故![]() ,
,
∴面![]() 与面
与面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.
【空间的角练习】
一、选择题
1.在正方体ABCD—A1B1C1D1中,M为DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设△ABC和△DBC所在两平面互相垂直,且AB=BC=BD=a,∠CBA=
∠CBD=120°,则AD与平面BCD所成的角为( )
A.30° B.45° C.60° D.75°
二、填空题
3.已知∠AOB=90°,过O点引∠AOB所在平面的斜线OC,与OA、OB分别成45°、60°,则以OC为棱的二面角A—OC—B的余弦值等于_________.
4.正三棱锥的一个侧面的面积与底面积之比为2∶3,则这个三棱锥的侧面和底面所成二面角的度数为_________.
三、解答题
5,已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小;
(3)求证:二面角B—PC—D为直二面角.

6.设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=
∠DBC=120°
求:(1)直线AD与平面BCD所成角的大小;
(2)异面直线AD与BC所成的角;
(3)二面角A—BD—C的大小.
7.一副三角板拼成一个四边形ABCD,如图,然后将它沿BC折成直二面角.

(1)求证:平面ABD⊥平面ACD;
(2)求AD与BC所成的角;
(3)求二面角A—BD—C的大小.
8.设D是△ABC的BC边上一点,把△ACD沿AD折起,使C点所处的新位置C′在平面ABD上的射影H恰好在AB上.
(1)求证:直线C′D与平面ABD和平面AHC′所成的两个角之和不可能超过90°;
(2)若∠BAC=90°,二面角C′—AD—H为60°,求∠BAD的正切值.

参考答案
一、1.解析:(特殊位置法)将P点取为A1,作OE⊥AD于E,连结A1E,则A1E为OA1的射影,又AM⊥A1E,∴AM⊥OA1,即AM与OP成90°角.
答案:D
2.解析:作AO⊥CB的延长线,连OD,则OD即为AD在平面BCD上的射影,
∵AO=OD=![]() a,∴∠ADO=45°.
a,∴∠ADO=45°.
答案:B
二、3.解析:在OC上取一点C,使OC=1,过C分别作CA⊥OC交OA于A,CB⊥OC交OB于B,则AC=1,,OA=![]() ,BC=
,BC=![]() ,OB=2,Rt△AOB中,AB2=6,△ABC中,由余弦定理,得cosACB=-
,OB=2,Rt△AOB中,AB2=6,△ABC中,由余弦定理,得cosACB=-![]() .
.
答案:-![]()
4.解析:设一个侧面面积为S1,底面面积为S,则这个侧面在底面上射影的面积为![]() ,由题设得
,由题设得![]() ,设侧面与底面所成二面角为θ,则cosθ=
,设侧面与底面所成二面角为θ,则cosθ=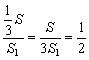 ,∴θ=60°.
,∴θ=60°.
答案:60°
三、5.(1)解:因为PA⊥平面AC,AB⊥BC,∴PB⊥BC,即∠PBC=90°,由勾股定理得PB=![]() .
.
∴PC=![]() .
.

(2)解:如图,过点C作CE∥BD交AD的延长线于E,连结PE,则PC与BD所成的角为∠PCE或它的补角.
∵CE=BD=![]() ,且PE=
,且PE=![]()
∴由余弦定理得cosPCE=![]()
∴PC与BD所成角的余弦值为![]() .
.
(3)证明:设PB、PC中点分别为G、F,连结FG、AG、DF,则GF∥BC∥AD,且GF=![]() BC=1=AD,从而四边形ADFG为平行四边形,
BC=1=AD,从而四边形ADFG为平行四边形,
又AD⊥平面PAB,∴AD⊥AG,即ADFG为矩形,DF⊥FG.
在△PCD中,PD=![]() ,CD=
,CD=![]() ,F为BC中点,∴DF⊥PC
,F为BC中点,∴DF⊥PC
从而DF⊥平面PBC,故平面PDC⊥平面PBC,即二面角B—PC—D为直二面角.
6.解:(1)如图,在平面ABC内,过A作AH⊥BC,垂足为H,则AH⊥平面DBC,
∴∠ADH即为直线AD与平面BCD所成的角.由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,

∴∠ADH=45°
(2)∵BC⊥DH,且DH为AD在平面BCD上的射影,
∴BC⊥AD,故AD与BC所成的角为90°.
(3)过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A—BD—C的平面角的补角.设BC=a,则由题设知,AH=DH=![]() ,在△HDB中,HR=
,在△HDB中,HR=![]() a,∴tanARH=
a,∴tanARH=![]() =2
=2
故二面角A—BD—C大小为π-arctan2.
7.(1)证明:取BC中点E,连结AE,∵AB=AC,∴AE⊥BC
∵平面ABC⊥平面BCD,∴AE⊥平面BCD,
∵BC⊥CD,由三垂线定理知AB⊥CD.
又∵AB⊥AC,∴AB⊥平面BCD,∵AB![]() 平面ABD.
平面ABD.
∴平面ABD⊥平面ACD.
(2)解:在面BCD内,过D作DF∥BC,过E作EF⊥DF,交DF于F,由三垂线定理知AF⊥DF,∠ADF为AD与BC所成的角.
设AB=m,则BC=![]() m,CE=DF=
m,CE=DF=![]() m,CD=EF=
m,CD=EF=![]() m
m
![]()
即AD与BC所成的角为arctan![]()
(3)解:∵AE⊥面BCD,过E作EG⊥BD于G,连结AG,由三垂线定理知AG⊥BD,
∴∠AGE为二面角A—BD—C的平面角

∵∠EBG=30°,BE=![]() m,∴EG=
m,∴EG=![]() m
m
又AE=![]() m,∴tanAGE=
m,∴tanAGE=![]() =2,∴∠AGE=arctan2.
=2,∴∠AGE=arctan2.
即二面角A—BD—C的大小为arctan2.
8.(1)证明:连结DH,∵C′H⊥平面ABD,∴∠C′DH为C′D与平面ABD所成的角且平面C′HA⊥平面ABD,过D作DE⊥AB,垂足为E,则DE⊥平面C′HA.
故∠DC′E为C′D与平面C′HA所成的角
∵sinDC′E=![]() ≤
≤![]() =sinDC′H
=sinDC′H
∴∠DC′E≤∠DC′H,
∴∠DC′E+∠C′DE≤∠DC′H+∠C′DE=90°
(2)解:作HG⊥AD,垂足为G,连结C′G,
则C′G⊥AD,故∠C′GH是二面角C′—AD—H的平面角
即∠C′GH=60°,计算得tanBAD=![]() .
.
空间的距离
【复习要点】
空间中距离的求法是历年高考考查的重点,其中以点与点、点到线、点到面的距离为基础,求其他几种距离一般化归为这三种距离.
空间中的距离主要指以下七种:
(1)两点之间的距离.
(2)点到直线的距离.
(3)点到平面的距离.
(4)两条平行线间的距离.
(5)两条异面直线间的距离.
(6)平面的平行直线与平面之间的距离.
(7)两个平行平面之间的距离.
七种距离都是指它们所在的两个点集之间所含两点的距离中最小的距离.七种距离之间有密切联系,有些可以相互转化,如两条平行线的距离可转化为求点到直线的距离,平行线面间的距离或平行平面间的距离都可转化成点到平面的距离.
在七种距离中,求点到平面的距离是重点,求两条异面直线间的距离是难点.
求点到平面的距离:(1)直接法,即直接由点作垂线,求垂线段的长.(2)转移法,转化成求另一点到该平面的距离.(3)体积法.
求异面直线的距离:(1)定义法,即求公垂线段的长.(2)转化成求直线与平面的距离.(3)函数极值法,依据是两条异面直线的距离是分别在两条异面直线上两点间距离中最小的.
【例题】
【例19】 如图,已知ABCD是矩形,AB=a,AD=b,PA⊥平面ABCD,PA=2c,Q是PA的中点.
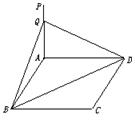
求:(1)Q到BD的距离;
(2)P到平面BQD的距离.
解:(1)在矩形ABCD中,作AE⊥BD,E为垂足
连结QE,∵QA⊥平面ABCD,由三垂线定理得QE⊥BE
∴QE的长为Q到BD的距离
在矩形ABCD中,AB=a,AD=b,
∴AE=![]()
在Rt△QAE中,QA=![]() PA=c
PA=c
∴QE=![]()
∴Q到BD距离为![]() .
.
(2)解法一:∵平面BQD经过线段PA的中点,
∴P到平面BQD的距离等于A到平面BQD的距离
在△AQE中,作AH⊥QE,H为垂足
∵BD⊥AE,BD⊥QE,∴BD⊥平面AQE ∴BD⊥AH
∴AH⊥平面BQE,即AH为A到平面BQD的距离.
在Rt△AQE中,∵AQ=c,AE=![]()
∴AH=![]()
∴P到平面BD的距离为![]()
解法二:设点A到平面QBD的距离为h,由
VA—BQD=VQ—ABD,得![]() S△BQD·h=
S△BQD·h=![]() S△ABD·AQ
S△ABD·AQ
h=![]()
【例20】 把正方形ABCD沿对角线AC折起成直二面角,点E、F分别是AD、BC的中点,点O是原正方形的中心,求:
(1)EF的长;
(2)折起后∠EOF的大小.
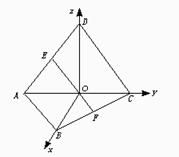 解:如图,以O点为原点建立空间直角坐标系O—xyz,设正方形ABCD边长为a,
解:如图,以O点为原点建立空间直角坐标系O—xyz,设正方形ABCD边长为a,
则A(0,-![]() a,0),B(
a,0),B(![]() a,0,0),C(0,
a,0,0),C(0,
![]() a,0),
a,0),
D(0,0,
![]() a),E(0,-
a),E(0,-![]() a, a),F(
a, a),F(![]() a,
a, ![]() a,0)
a,0)
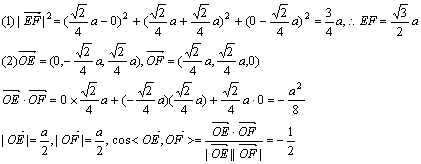
∴∠EOF=120°
【例21】 正方体ABCD—A1B1C1D1的棱长为1,求异面直线A1C1与AB1间的距离.
解法一:如图,连结AC1,在正方体AC1中,∵A1C1∥AC,∴A1C1∥平面AB1C,∴A1C1与平面AB1C间的距离等于异面直线A1C1与AB1间的距离.
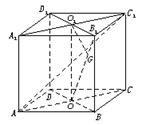
连结B1D1、BD,设B1D1∩A1C1=O1,BD∩AC=O
∵AC⊥BD,AC⊥DD1,∴AC⊥平面BB1D1D
∴平面AB1C⊥平面BB1D1D,连结B1O,则平面AB1C∩平面BB1D1D=B1O
作O1G⊥B1O于G,则O1G⊥平面AB1C
∴O1G为直线A1C1与平面AB1C间的距离,即为异面直线A1C1与AB1间的距离.
在Rt△OO1B1中,∵O1B1=![]() ,OO1=1,∴OB1=
,OO1=1,∴OB1=![]() =
= ![]()
∴O1G=![]() ,即异面直线A1C1与AB1间距离为
,即异面直线A1C1与AB1间距离为![]() .
.
解法二:如图,在A1C上任取一点M,作MN⊥AB1于N,作MR⊥A1B1于R,连结RN,
∵平面A1B1C1D1⊥平面A1ABB1,∴MR⊥平面A1ABB1,MR⊥AB1
∵AB1⊥RN,设A1R=x,则RB1=1-x
∵∠C1A1B1=∠AB1A1=45°,
∴MR=x,RN=NB1=![]()
![]() (0<x<1
(0<x<1![]()
∴当x=![]() 时,MN有最小值
时,MN有最小值![]() 即异面直线A1C1与AB1距离为
即异面直线A1C1与AB1距离为![]() .
.
【例22】
如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形,![]() ,侧棱
,侧棱![]() ,
,![]() 、
、![]() 分别是
分别是![]() 与
与![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 上的射影是
上的射影是![]() 的的重心
的的重心![]() 。
。
(1)
求![]() 与平面
与平面![]() 所成角的大小(结果用反三角函数值表示);
所成角的大小(结果用反三角函数值表示);
(2)
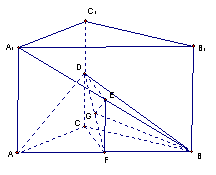 求点
求点![]() 到平面
到平面![]() 的距离。
的距离。
解:(1)连接![]() ,
,
则![]() 即为
即为![]() 与平面
与平面![]() 所成的角,
所成的角,
设![]() ,
,![]() ,
,
在![]() 中,
中,![]()
则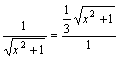 ,
,
 ∴
∴![]()
则![]()
∴![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() 。
。
(2)、设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
∵![]() ,
,
∴![]()
由![]() ,
,
即![]() 。
。
【例23】 如图,在三棱柱ABC—A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°.
(1)求证:平面CA1B⊥平面A1ABB1
(2)求直线A1C与平面BCC1B1所成角的正切值;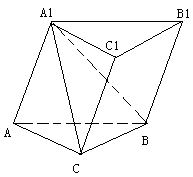
(3)求点C1到平面A1CB的距离.
证:(Ⅰ)因为四边形BCC1B1是矩形∴BC⊥BB1,
又∵AB⊥BC,∴BC⊥平面A1ABB1,
∵BC![]() 平面CA1B,∴平面CA1B⊥平面A1ABB1.
平面CA1B,∴平面CA1B⊥平面A1ABB1.
解(2)过A1作A1D⊥B1B于D,连接DC,
∵BC⊥平面A1ABB1,∴BC⊥A1D
∴A1D⊥平面BCC1B1,故∠A1CD为直线A1C与平面BCC1B1所成的角.
在矩形BCC1B1中,DC=![]() ,
,
因为四边形A1ABB1是菱形,∠A1AB=60°,CB=3,
AB=4,∴![]() ,
,
![]()
(3)∵B1C1∥BC1, ∴B1C1∥平面A1BC,
∴C1到平面A1BC的距离即为B1到平面A1BC的距离.
连结AB1 ,AB1与A1B交于点O,∵四边形A1ABB1是菱形,∴B1O⊥A1B.
∵平面CA1B⊥平面A1ABB1,∴ B1O⊥平面A1BC
∵B1O即为C1到平面A1BC的距离.
∵B1O=![]() ,
,
∴C1到平面A1BC的距离为![]() .
.
【例24】 如图,四棱锥P—ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60°,在四边形ABCD中,∠D=∠DAB=90°,AB=4,CD=1,AD=2.
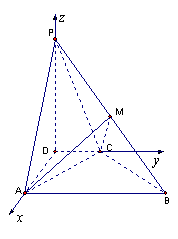 (1)建立适当的坐标系,并写出点B、P的坐标;
(1)建立适当的坐标系,并写出点B、P的坐标;
(2)求异面直线PA与BC所成的角;
(3)若PB的中点为M,求证:平面AMC⊥平面PBC.
解(1)建立如图所示的空间直角坐标系![]()
∵∠D=∠DAB=90°,AB=4,CD=1,AD=2,
∴A(2,0,0),C(0,1,0),B(2,4,0).
由PD⊥平面ABCD,得∠PAD为PA与平面ABCD所成的角,∴∠PAD=60°.
在Rt△PAD中,由AD=2,得PD=![]() ,
,
∴![]() .
.
(2)![]()
![]()
所以PA与BC所成的角为![]()
(3)![]() .
.
![]()
![]() ,
,
![]()
![]()
![]() .
.
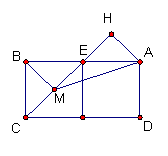
【例25】
如图,在矩形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,将
上一点,将![]() 点沿线段
点沿线段![]() 折起至点
折起至点![]() ,连结
,连结![]()
![]() ,取
,取![]() 的中点
的中点![]() ,若有
,若有![]() 平面
平面![]() .
.
(1)试确定![]() 点位置;
点位置;
(2)若异面直线![]() 所成的角为
所成的角为![]() ,求证:平面
,求证:平面![]() ⊥平面
⊥平面![]() ;
;
 (3)在条件(2)下,求点
(3)在条件(2)下,求点![]() 到平面
到平面![]() 的距离.
的距离.
解:(1)![]() 为
为![]() 的中点.证明如下:
的中点.证明如下:
取![]() 的中点
的中点![]() ,连
,连![]() .
.
由条件知![]() ,
,![]() .
.
则![]() 四点共面.
四点共面.
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() .
.
 则四边形
则四边形![]() 为平行四边形.
为平行四边形.
![]() .
.
则![]() 为
为![]() 的中点.
的中点.
(2)
![]() 所成的角为
所成的角为![]() ,
,
![]() .
.
![]() ,
,![]() .
.
 在
在![]() 中,
中,![]() .
.
![]() ,
,![]() .
.
则![]() .
.![]() .
.
![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(3)![]() 平面
平面![]() ,
,![]() 点
点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
作![]() 交
交![]() 的延长线于
的延长线于![]() ,
,
![]() 平面
平面![]() ⊥平面
⊥平面![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() 点
点![]() 到平面
到平面![]() 的距离即点
的距离即点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
【例26】 已知斜三棱柱ABC—A1B1C1,∠BCA=90°,AC=BC=a,A1在底面ABC上的射影恰为AC的中点D,又A1B⊥AC1.
(1)求证:BC⊥平面ACC1A1;
(2)求AA1与平面ABC所成的角;
(3)求二面角B-AA1-C的正切值.
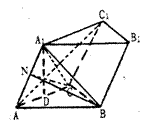 解:(1)证明:∵A1D⊥平面ABC,∴A1D⊥BC(2分)
解:(1)证明:∵A1D⊥平面ABC,∴A1D⊥BC(2分)
又∵AC⊥BC,∴BC⊥平面ACC1A1(4分)
(2)∵A1D⊥平面ABC,
∴∠A1AD是AA1与底面ABC所成的角
由(1)知,BC⊥平面ACC1A1,又A1B⊥AC1
∴A1C⊥AC1,∴ACC1A1是菱形 ∴AA1=a,
∵A1D⊥AC,且AD=DC=![]() a,∴∠A1AD=60°即AA1与底面ABC所成的角为60°
a,∴∠A1AD=60°即AA1与底面ABC所成的角为60°
(3)由(1)知,BC⊥平面ACC1A1,作CN⊥AA1于点N,
∵ΔA1AC是等边三角形,∴点N是AA1的中点,连NB,则BN⊥AA1,
∴∠BNC是二面角B-AA1-C的平面角
易知,CN=![]() ,BC=a
,BC=a
∴在RtΔBCN中,tan∠BNC=![]() ,
,
∴二面角B-AA1-C的正切值为![]()
【例27】 对棱都相等的四面体称为等腰四面体。
(1)试在长方体![]() 中,连接某些顶点作出一个等腰四面体,写作
中,连接某些顶点作出一个等腰四面体,写作
![]() ,并探索等腰四面体的性质。(至少写出三条,不需证明)
,并探索等腰四面体的性质。(至少写出三条,不需证明)
 性质:①四个面都是全等的三角形;
性质:①四个面都是全等的三角形;
②各顶点到其所对面的距离都相等;
③它的体积是长方体体积的三分之一。
(2)证明等腰四面体的另一条性质:
等腰四面体中,各侧面与底面所成二面角的余弦之和等于1。
已知:四面体![]() 中,
中,
![]() ,各侧面与底面所成二面角分
,各侧面与底面所成二面角分 别为
别为![]() 。
。
求证:![]()
证明:过![]() 作
作![]() 底面
底面![]() ,
,![]() 为垂足,
为垂足,
连接![]() ,
,
设二面角![]() 为
为![]() ,则
,则![]() ,
,
设二面角![]() 为
为![]() ,
,
则![]() ,
,
设二面角![]() 为
为![]() ,则
,则![]() ,
,
![]()
![]()
![]()
![]()
【空间的距离练习】
一、选择题
1.正方形ABCD边长为2,E、F分别是AB和CD的中点,将正方形沿EF折成直二面角(如图),M为矩形AEFD内一点,如果∠MBE=∠MBC,MB和平面BCF所成角的正切值为![]() ,那么点M到直线EF的距离为( )
,那么点M到直线EF的距离为( )
![]()
2.三棱柱ABC—A1B1C1中,AA1=1,AB=4,BC=3,∠ABC=90°,设平面A1BC1与平面ABC的交线为l,则A1C1与l的距离为( )
A.![]() B.
B.![]() C.2.6 D.2.4
C.2.6 D.2.4
二、填空题
3.如左下图,空间四点A、B、C、D中,每两点所连线段的长都等于a,动点P在线段AB上,动点Q在线段CD上,则P与Q的最短距离为_________.
4.如右上图,ABCD与ABEF均是正方形,如果二面角E—AB—C的度数为
30°,那么EF与平面ABCD的距离为_________.
三、解答题
5.在长方体ABCD—A1B1C1D1中,AB=4,BC=3,CC1=2,如图:
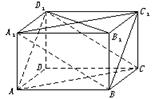
(1)求证:平面A1BC1∥平面ACD1;
(2)求(1)中两个平行平面间的距离;
(3)求点B1到平面A1BC1的距离.
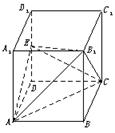 6.已知正四棱柱ABCD—A1B1C1D1,点E在棱D1D上,截面EAC∥D1B且面EAC与底面ABCD所成的角为45°,AB=a,求:
6.已知正四棱柱ABCD—A1B1C1D1,点E在棱D1D上,截面EAC∥D1B且面EAC与底面ABCD所成的角为45°,AB=a,求:
(1)截面EAC的面积;
(2)异面直线A1B1与AC之间的距离;
(3)三棱锥B1—EAC的体积.
7.如图,已知三棱柱A1B1C1—ABC的底面是边长为2的正三角形,侧棱A1A与AB、AC均成45°角,且A1E⊥B1B于E,A1F⊥CC1于F.
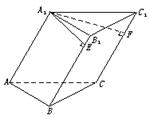
(1)求点A到平面B1BCC1的距离;
(2)当AA1多长时,点A1到平面ABC与平面B1BCC1的距离相等.
8.如图,在梯形ABCD中,AD∥BC,∠ABC=![]() ,AB=
,AB= ![]() AD=a,
AD=a,
∠ADC=arccos![]() ,PA⊥面ABCD且PA=a.
,PA⊥面ABCD且PA=a.
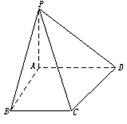
(1)求异面直线AD与PC间的距离;
(2)在线段AD上是否存在一点F,使点A到平面PCF的距离为![]() .
.
【空间的距离参考答案】
一、1.解析:过点M作MM′⊥EF,则MM′⊥平面BCF
∵∠MBE=∠MBC
∴BM′为∠EBC为角平分线,
∴∠EBM′=45°,BM′=![]() ,从而MN=
,从而MN=![]()
答案:A
2.解析:交线l过B与AC平行,作CD⊥l于D,连C1D,则C1D为A1C1与l的距离,而CD等于AC上的高,即CD=![]() ,Rt△C1CD中易求得C1D=
,Rt△C1CD中易求得C1D=![]() =2.6
=2.6
答案:C
二、3.解析:以A、B、C、D为顶点的四边形为空间四边形,且为正四面体,取P、Q分别为AB、CD的中点,因为AQ=BQ=![]() a,∴PQ⊥AB,同理可得PQ⊥CD,故线段PQ的
a,∴PQ⊥AB,同理可得PQ⊥CD,故线段PQ的
长为P、Q两点间的最短距离,在Rt△APQ中,PQ=![]() a
a
答案:![]() a
a
4.解析:显然∠FAD是二面角E—AB—C的平面角,∠FAD=30°,过F作FG⊥平面ABCD于G,则G必在AD上,由EF∥平面ABCD.
∴FG为EF与平面ABCD的距离,即FG=![]() .
.
答案:![]()
三、5.(1)证明:由于BC1∥AD1,则BC1∥平面ACD1
同理,A1B∥平面ACD1,则平面A1BC1∥平面ACD1
(2)解:设两平行平面A1BC1与ACD1间的距离为d,则d等于D1到平面A1BC1的距离.易求A1C1=5,A1B=2![]() ,BC1=
,BC1=![]() ,则cosA1BC1=
,则cosA1BC1=![]() ,则sinA1BC1=
,则sinA1BC1=![]() ,则S
,则S![]() =
=![]() ,由于
,由于![]() ,则
,则![]() S
S![]() ·d=
·d=![]() ·BB1,代入求得d=
·BB1,代入求得d=![]() ,即两平行平面间的距离为
,即两平行平面间的距离为![]() .
.
(3)解:由于线段B1D1被平面A1BC1所平分,则B1、D1到平面A1BC1的距离相等,则由(2)知点B1到平面A1BC1的距离等于![]() .
.
6.解:(1)连结DB交AC于O,连结EO,
∵底面ABCD是正方形
∴DO⊥AC,又ED⊥面ABCD
∴EO⊥AC,即∠EOD=45°
又DO=![]() a,AC=
a,AC=![]() a,EO=
a,EO=![]() =a,∴S△EAC=
=a,∴S△EAC=![]() a
a
(2)∵A1A⊥底面ABCD,∴A1A⊥AC,又A1A⊥A1B1
∴A1A是异面直线A1B1与AC间的公垂线
又EO∥BD1,O为BD中点,∴D1B=2EO=2a
∴D1D=![]() a,∴A1B1与AC距离为
a,∴A1B1与AC距离为![]() a
a
(3)连结B1D交D1B于P,交EO于Q,推证出B1D⊥面EAC
∴B1Q是三棱锥B1—EAC的高,得B1Q=![]() a
a
![]()
7.解:(1)∵BB1⊥A1E,CC1⊥A1F,BB1∥CC1
∴BB1⊥平面A1EF
即面A1EF⊥面BB1C1C
在Rt△A1EB1中,
∵∠A1B1E=45°,A1B1=a
∴A1E=![]() a,同理A1F=
a,同理A1F=![]() a,又EF=a,∴A1E=
a,又EF=a,∴A1E=![]() a
a
同理A1F=![]() a,又EF=a
a,又EF=a
∴△EA1F为等腰直角三角形,∠EA1F=90°
过A1作A1N⊥EF,则N为EF中点,且A1N⊥平面BCC1B1
即A1N为点A1到平面BCC1B1的距离
∴A1N=![]()
又∵AA1∥面BCC1B,A到平面BCC1B1的距离为![]()
∴a=2,∴所求距离为2
(2)设BC、B1C1的中点分别为D、D1,连结AD、DD1和A1D1,则DD1必过点N,易证ADD1A1为平行四边形.
∵B1C1⊥D1D,B1C1⊥A1N
∴B1C1⊥平面ADD1A1
∴BC⊥平面ADD1A1
得平面ABC⊥平面ADD1A1,过A1作A1M⊥平面ABC,交AD于M,
若A1M=A1N,又∠A1AM=∠A1D1N,∠AMA1=∠A1ND1=90°
∴△AMA1≌△A1ND1,∴AA1=A1D1=![]() ,即当AA1=
,即当AA1=![]() 时满足条件.
时满足条件.
8.解:(1)∵BC∥AD,BC![]() 面PBC,∴AD∥面PBC
面PBC,∴AD∥面PBC
从而AD与PC间的距离就是直线AD与平面PBC间的距离.
过A作AE⊥PB,又AE⊥BC
∴AE⊥平面PBC,AE为所求.
在等腰直角三角形PAB中,PA=AB=a
∴AE=![]() a
a
(2)作CM∥AB,由已知cosADC=![]()
∴tanADC=![]() ,即CM=
,即CM=![]() DM
DM
∴ABCM为正方形,AC=![]() a,PC=
a,PC=![]() a
a
过A作AH⊥PC,在Rt△PAC中,得AH=![]()
下面在AD上找一点F,使PC⊥CF
取MD中点F,△ACM、△FCM均为等腰直角三角形
∴∠ACM+∠FCM=45°+45°=90°
∴FC⊥AC,即FC⊥PC∴在AD上存在满足条件的点F.