08高考数学第二轮复习集合与简易逻辑
一、【重点知识结构】


二、【高考要求】
1. 理解集合、子集、交集、并集、补集的概念.了解空集和全集的意义,了解属于、包含、相等关系的意义,能掌握有关的述语和符号,能正确地表示一些较简单的集合.
2. 理解ax+b<c,ax+b>c(c>0)型不等式的概念,并掌握它们的解法.了解二次函数、一元二次不等式及一元二次方程三者之间的关系,掌握一元二次不等式及简单分式不等式的解法.
3. 理解逻辑联结词“或”、“且”、“非”的含义;理解四种命题及其相互关系;掌握充要条件的意义和判定.
4. 学会运用数形结合、分类讨论的思想方法分析和解决有关集合问题,形成良好的思维品质;学会判断和推理,解决简易逻辑问题,培养逻辑思维能力.
三、【高考热点分析】
集合与简易逻辑是高中数学的重要基础知识,是高考的必考内容.本章知识的高考命题热点有以下两个方面:一是集合的运算、集合的有关述语和符号、集合的简单应用、判断命题的真假、四种命题的关系、充要条件的判定等作基础性的考查,题型多以选择、填空题的形式出现;二是以函数、方程、三角、不等式等知识为载体,以集合的语言和符号为表现形式,结合简易逻辑知识考查学生的数学思想、数学方法和数学能力,题型常以解答题的形式出现.
四、【高考复习建议】
概念多是本章内容的一大特点,一是要抓好基本概念的过关,一些重点知识(如子、交、并、补集及充要条件等)要深刻理解和掌握;二是各种数学思想和数学方法在本章题型中都有较好体现,特别是数形结合思想,要善于运用韦氏图、数轴、函数图象帮助分析和理解集合问题.
五、【例 题】
【例1】
设![]() ,求集合A与B之间的关系。
,求集合A与B之间的关系。
解:由![]() ,得A=
,得A=![]()
![]()
![]()
∴A=B
【例2】
已知集合A=![]() ,集合B=
,集合B=![]() ,若B
,若B![]() A,求实数p
A,求实数p
的取值范围。
解:若B=Φ时,![]()
若B≠Φ时,则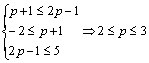
综上得知:![]() 时,B
时,B![]() A。
A。
【例3】
已知集合![]() ,集合B=
,集合B=![]() 。如果
。如果![]() ,
,
试求实数a的值。
解:注意集合A、B的几何意义,先看集合B;
当a=1时,B=Φ,A∩B=Φ
当a=-1时,集合B为直线y=-15,A∩B=Φ
当a≠±1时,集合A:![]() ,
,![]() ,只有
,只有![]() 才满足条件。
才满足条件。
故![]() ;解得:a=-5或a=
;解得:a=-5或a=![]()
∴a=1或a=![]() 或a=-1或a=-5。
或a=-1或a=-5。
【例4】
若集合A=![]() ,B=
,B=![]() ,且
,且![]() ,求实数x。
,求实数x。
解:由题设知![]() ,∴
,∴![]() ,故
,故![]() 或
或![]()
即![]() 或
或![]() 或
或![]() ,但当
,但当![]() 时,
时,![]() 不满足集合A的条件。
不满足集合A的条件。
∴实数x的值为![]() 或
或![]() 。
。
【例5】
已知集合A=![]() ,B=
,B=![]() ,若
,若![]() ,求实数m的值。
,求实数m的值。
解:不难求出A=![]() ,由
,由![]()
![]() ,又
,又![]() ,
,![]()
①若![]() ,即
,即![]() ,则
,则![]()
②若![]() ,即
,即![]() ,
,![]() ,
,
∴![]()
![]()
故由①②知:m的取值范围是![]()
注:不要忽略空集是任何集合的子集。
【例6】
已知集合A={![]() },B=
},B=![]() ,C=
,C=![]() ,
,
若![]() 与
与![]() 同时成立,求实数a的值。
同时成立,求实数a的值。
解:易求得B=![]() ,C=
,C=![]() ,由
,由![]() 知A与B的交集为非空集。
知A与B的交集为非空集。
故2,3两数中至少有一适合方程![]()
又![]() ,∴
,∴![]() ,即
,即![]() 得,a=5或a=-2
得,a=5或a=-2
当a=5时,A=![]() ,于是
,于是![]() ,故a=5舍去。
,故a=5舍去。
当a=-2时,A=![]() ,于是
,于是![]() ,∴a=-2。
,∴a=-2。
【例7】
![]() ,
,![]() ,A∪B=A,求a的取值构成的集合。
,A∪B=A,求a的取值构成的集合。
解:∵A∪B=A,∴![]() ,当
,当![]() 时
时![]() ,∴-4<a<4,
,∴-4<a<4,
![]() ,当1∈B时,将x=1代入B中方程得a=4,此时B={1},当2∈B时,将x=2代入B中方程得a=5,此时
,当1∈B时,将x=1代入B中方程得a=4,此时B={1},当2∈B时,将x=2代入B中方程得a=5,此时![]() ,a=5舍去,∴-4<a≤4。
,a=5舍去,∴-4<a≤4。
【例8】
已知![]() ,
,![]() 且A∪B=A,求实数a组成的集合C。
且A∪B=A,求实数a组成的集合C。
解:由A={1,2},由A∪B=A,即![]() ,只需a×1-2=0,a=2或a×2-2=0,a=1。
,只需a×1-2=0,a=2或a×2-2=0,a=1。
另外显然有当a=0时,![]() 也符合。所以C={0,1,2}。
也符合。所以C={0,1,2}。
【例9】 某车间有120人,其中乘电车上班的84人,乘汽车上班的32人,两车都乘的18人,求:
 (1)只乘电车的人数;(2)不乘电车的人数;(3)乘车的人数;
(1)只乘电车的人数;(2)不乘电车的人数;(3)乘车的人数;
(4)不乘车的人数;(5)只乘一种车的人数。
解:本题是已知全集中元素的个数,求各部分元素的个数,可用图解法。设只乘电车的人数为x人,不乘电车的人数为y人,乘车的人数为z人,不乘车的人数为u人,只乘一种车的人数为v人
如图所示(1)x=66人,(2)y=36人,(3)z=98人,(4)u=22人,(5)v=80人。
【例10】
(2004届湖北省黄冈中学高三数学综合训练题)已知M是关于![]() 的不等式
的不等式![]() 的解集,且M中的一个元素是0,求实数
的解集,且M中的一个元素是0,求实数![]() 的取值范围,并用
的取值范围,并用![]() 表示出该不等式的解集.
表示出该不等式的解集.
解:原不等式即![]() ,
,
由![]() 适合不等式故得
适合不等式故得![]() ,所以
,所以![]() ,或
,或![]() .
.
若![]() ,则
,则![]() ,∴
,∴![]() ,
,
此时不等式的解集是![]() ;
;
若![]() ,由
,由![]() ,∴
,∴![]() ,
,
此时不等式的解集是![]() .
.
【例11】 (2004届杭州二中高三数学综合测试题)已知![]() ,设命题
,设命题![]() ,命题
,命题![]() .试寻求使得
.试寻求使得![]() 都是真命题的
都是真命题的![]() 的集合.
的集合.
解:设![]() ,
,
依题意,求使得![]() 都是真命题的
都是真命题的![]() 的集合即是求集合
的集合即是求集合![]() ,
,
∵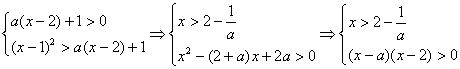
∴若![]() 时,则有
时,则有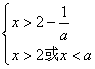 ,
,
而![]() ,所以
,所以![]() ,
,
即当![]() 时使
时使![]() 都是真命题的
都是真命题的![]() ;
;
当![]() 时易得使
时易得使![]() 都是真命题的
都是真命题的![]() ;
;
若![]() ,则有
,则有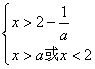 ,
,
此时使得![]() 都是真命题的
都是真命题的![]() .
.
综合略.
【例12】
(2004届湖北省黄冈中学综合测试题)已知条件![]() 和条件
和条件![]() ,请选取适当的实数
,请选取适当的实数![]() 的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
分析:本题为一开放性命题,由于能得到的答案不唯一,使得本题的求解没有固定的模式,考生既能在一般性的推导中找到一个满足条件的![]() ,也能先猜后证,所找到的实数
,也能先猜后证,所找到的实数![]() 只需满足
只需满足![]() ,且
,且![]() 1即可.这种新颖的命题形式有较强的综合性,同时也是对于四个命题考查的一种新尝试,如此命题可以考查学生探究问题、解决问题的能力,符合当今倡导研究性学习的教学方向.
1即可.这种新颖的命题形式有较强的综合性,同时也是对于四个命题考查的一种新尝试,如此命题可以考查学生探究问题、解决问题的能力,符合当今倡导研究性学习的教学方向.
解:已知条件![]() 即
即![]() ,或
,或![]() ,∴
,∴![]() ,或
,或![]() ,
,
已知条件![]() 即
即![]() ,∴
,∴![]() ,或
,或![]() ;
;
令![]() ,则
,则![]() 即
即![]() ,或
,或![]() ,此时必有
,此时必有![]() 成立,反之不然.
成立,反之不然.
故可以选取的一个实数是![]() ,A为
,A为![]() ,B为
,B为![]() ,对应的命题是若
,对应的命题是若![]() 则
则![]() ,
,
由以上过程可知这一命题的原命题为真命题,但它的逆命题为假命题.
【例13】
已知![]() ;¬
;¬![]() 是¬
是¬![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
解:由![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,
,
∴¬![]() 即
即![]() ,或
,或![]() ,而¬
,而¬![]() 即
即![]() ,或
,或![]()
![]() ;
;
由¬![]() 是¬
是¬![]() 的必要不充分条件,知¬
的必要不充分条件,知¬![]()
![]() ¬
¬![]() ,
,
设A=![]() ,B=
,B=![]() ,
,
则有A![]() ,故
,故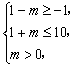 且不等式中的第一、二两个不等式不能同时取等号,
且不等式中的第一、二两个不等式不能同时取等号,
解得![]() ,此即为“¬
,此即为“¬![]() 是¬
是¬![]() 的必要不充分条件”时实数
的必要不充分条件”时实数![]() 的取值范围.
的取值范围.
【例14】
(2004届全国大联考高三第四次联考试题)已知函数![]() ,其中
,其中![]() .
.
(1)判断函数![]() 的增减性;
的增减性;
(2)(文)若命题![]()
![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
(2)(理)若命题![]()
![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围.
的取值范围.
解:(1)∵![]() ,∴
,∴![]() ,
,
即![]() ,∴函数
,∴函数![]() 是增函数;
是增函数;
(2)(文)![]() 即
即![]() ,必有
,必有![]() ,
,
当![]() ,
,![]() ,不等式化为
,不等式化为![]() ,
,
∴![]() ,这显然成立,此时
,这显然成立,此时![]() ;
;
当![]() 时,
时,![]() ,不等式化为
,不等式化为![]() ,
,
∴![]() ,故
,故![]() ,此时
,此时![]() ;
;
综上所述知,使命题![]() 为真命题的
为真命题的![]() 的取值范围是
的取值范围是![]() .
.
(2)(理)![]() 即
即![]() ,必有
,必有![]() ,
,
当![]() 时,
时,![]() ,不等式化为
,不等式化为![]() ,
,
∴![]() ,故
,故![]() ,∴
,∴![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,不等式化为
,不等式化为![]() ,
,
∴![]() ,这显然成立,此时
,这显然成立,此时![]() ;
;
当![]() 时,
时,![]() ,不等式化为
,不等式化为![]() ,
,
∴![]() ,故
,故![]() ,此时
,此时![]() ;
;
综上所述知,使命题![]() 为真命题的
为真命题的![]() 的取值范围是
的取值范围是![]() .
.
六、【专题练习】
一、选择题
1.已知I为全集,集合M、NÌI,若MÈN=M,则有:(D)
A.MÍ(![]() ) B.MÊ(
) B.MÊ(![]() ) C.
) C.![]() D.
D.![]()
2.若非空集合A、B适合关系AÌB,I是全集,下列集合为空集的是:(D)
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
3.已知集合A={0,1,2,3,4},B={0,2,4,8},那么A∩B子集的个数是:(C)
A.6个 B.7个 C.8个 D.9个
4.满足{a}![]() X
X![]() {a,b,c}的集合X的个数有 ( B )
{a,b,c}的集合X的个数有 ( B )
(A)2 (B)3 (C)4 (D)5
5.已知集合I、P、Q适合I=P![]() Q={1,2,3,4,5},P
Q={1,2,3,4,5},P![]() Q={1,2}则(P
Q={1,2}则(P![]() Q)
Q)![]() (
(![]()
![]()
![]() )
)
为( C )
(A){1,2,3} (B){2,3,4} (C){3,4,5} (D){1,4,5}
6.已知I为全集·集合M,N是I的子集M![]() N=N,则 ( B )
N=N,则 ( B )
(A)![]() (B)
(B)![]() (C)M
(C)M![]() (
(![]() )
(D)M
)
(D)M![]() (
(![]() )
)
7.设P={x x≥-2},Q={x
x≥3},则P![]() Q等于 ( D )
Q等于 ( D )
(A)Æ (B)R (C)P (D)Q
8.设集合E={nn=2k , k![]() Z},F={nn=4k , k
Z},F={nn=4k , k![]() Z},则E、F的关系是 (
B )
Z},则E、F的关系是 (
B )
(A)E![]() F
(B)E
F
(B)E![]() F (C)E=F (D)E
F (C)E=F (D)E![]() F=Æ
F=Æ
9.已知集合M=![]() ,N={ x x -1≤2},则M
,N={ x x -1≤2},则M![]() N等于 ( B )
N等于 ( B )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
10.已知集合I=R,集合M={ x
x =![]() ,n
,n![]() N},P={ x x =
N},P={ x x =![]() ,n
,n![]() N},则M与P的关系是 (
B )
N},则M与P的关系是 (
B )
(A)M![]() P=Æ (B)
P=Æ (B)![]()
![]() P=Æ (C)M
P=Æ (C)M![]()
![]() =Æ (D)
=Æ (D)![]()
![]()
![]() =Æ
=Æ
11.已知集合A={yy=![]() , x
, x ![]() R},B={yy=
R},B={yy=![]() x
x ![]() R},则A
R},则A![]() B等于 ( C )
B等于 ( C )
(A){2,4} (B){(2,4),(4,16)}
(C){ yy ≥0} (D){ x x<0}
12.设全集I=R,集合P=![]() ,集合Q={ x x+4>0},则 ( D )
,集合Q={ x x+4>0},则 ( D )
(A)P![]() Q=Æ (B)P
Q=Æ (B)P![]() Q=R
Q=R
(C)![]()
![]() Q=
Q=![]() (D)
(D)![]()
![]()
![]() ={-4}
={-4}
二、解答题
1、设A=![]() ,B=
,B=![]() ;若A
;若A![]() B,求实数a的取值范围。
B,求实数a的取值范围。
 解:由图象法解得:
解:由图象法解得:
当a>0时,![]() ;
;
当a≤0时,![]()
∴要使得A![]() B,必须且只须
B,必须且只须![]() ,解得
,解得![]()
2、已知A=![]() ,B=
,B=![]() 。若A
。若A![]() B,求实数a的取值范围。
B,求实数a的取值范围。
解:易得![]() ,由
,由![]() 得
得![]()
⑴当3a+1>2,即![]() 时,
时,![]()
要使A![]() B,必须
B,必须![]() ,
,
⑵当3a+1=2,即![]() 时,
时,![]() ;要使A
;要使A![]() B,a=1
B,a=1
当3a+1<2,即![]() 时,
时,![]()
⑶要使A![]() B,必须
B,必须![]()
综上知:![]() 或
或![]()
3、已知集合A=![]() ,B=
,B=![]() ,且
,且![]() ,求实数
,求实数
m的值。
解:![]() ,
,![]() ,由
,由![]() 得:
得:![]()
4、已知集合A=![]() ,B=
,B=![]() ;若
;若
![]() ,求实数a的取值范围。
,求实数a的取值范围。
解:B=![]() ,由
,由![]() 得:
得:![]()
因为![]() ,所以A=
,所以A=![]() 。
。
由![]() 得:
得:![]() 或
或![]()
所以![]()
5、已知集合![]() ,
,![]() 同时满足
同时满足
①![]() ,②
,②![]() ,其中p、q均为不等于零的实数,求p、q的值。
,其中p、q均为不等于零的实数,求p、q的值。
解:条件①是说集合A、B有相同的元素,条件②是说-2∈A但![]() ,A、B是两个方程的解集,方程
,A、B是两个方程的解集,方程![]() 和
和![]() 的根的关系的确定是该题的突破口。
的根的关系的确定是该题的突破口。
设![]() ,则
,则![]() ,否则将有q=0与题设矛盾。于是由
,否则将有q=0与题设矛盾。于是由![]() ,两边同除以
,两边同除以![]() ,得
,得![]() ,
,
知![]() ,故集合A、B中的元素互为倒数。
,故集合A、B中的元素互为倒数。
由①知存在![]() ,使得
,使得![]() ,且
,且![]() ,得
,得![]() 或
或![]() 。
。
由②知A={1,-2}或A={-1,-2}。
若A={1,-2},则![]() ,
,
有![]()
同理,若A={-1,-2},则![]() ,得p=3,q=2。
,得p=3,q=2。
综上,p=1,q=-2或p=3,q=2。
6、已知关于x的不等式![]() ,
,![]() 的解集依次为A、B,且
的解集依次为A、B,且![]() 。求实数a的取值范围。
。求实数a的取值范围。
解:![]() ,B={x(x-2)[x-(3a+1)]≤0}
,B={x(x-2)[x-(3a+1)]≤0}
∵![]()
①当3a+1≥2时,B={x2≤x≤3a+1}
∴3a+1<2a或![]() ,∴
,∴![]()
②当3a+1<2时,B={x3a+1≤x≤2}
∴2a>2或![]() ,∴
,∴![]()
7、已知集合![]() ,若
,若![]() ,且
,且![]() ,求实数a。
,求实数a。
解:∵A∪B=A,∴![]() 。
。
∵A={1,2},∴![]() 或B={1}或B={2}或B={1,2}。
或B={1}或B={2}或B={1,2}。
若![]() ,则由△<0知,不存在实数a使原方程有解;
,则由△<0知,不存在实数a使原方程有解;
若B={1},则由△=0得,a=2,此时1是方程的根;
若B={2},则由△=0得,a=2,此时2不是方程的根,
∴不存在实数a使原方程有解;
若B={1,2},则由△>0,得a∈R,且a≠2,
此时将x=1代入方程得a∈R,将x=2代入方程得a=3。
综上所述,实数a的值为2或3。