08高考文科数学二月月考试题
数学试题(文科)
考试时间:120分钟 满分:150分 考试内容:全部
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.设集合![]() ,则下列关系中不正确的是( )
,则下列关系中不正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.给出两个命题:p: x=x的充要条件是x为正实数;q: 存在反函数的函数一定是单调函数.则下列复合命题中的真命题是( )
A.p且q B.p或q C.┓p且q D.┓p或q
3.已知向量![]() ,
,![]() ,则
,则![]() 与
与![]() ( )
( )
A.垂直 B.不垂直也不平行 C.平行且同向 D.平行且反向
4.不等式![]() 的解集为( )
的解集为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
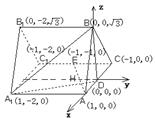
5.双曲线x2-y2=4的两条渐进线和直线x=2围成一个三角形区域(含边界),则该区域可
表示为( )
A.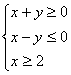 B.
B.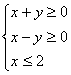 C.
C.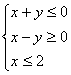 D.
D.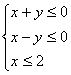
6.已知数列{an}对于任意m、n∈N*,有am+an=am+n,若![]() 则a40等于( )
则a40等于( )
A.8 B.9 C.10 D.11
7.已知定义域为R的函数![]() 在区间
在区间![]() 上为减函数,且函数
上为减函数,且函数![]() 为偶函数,则( )
为偶函数,则( )
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
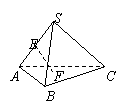
8.如图,在正四面体S—ABC中,E为SA的中点,F为DABC
的中心,则异面直线EF与AB所成的角是( )
A.30° B.45° C.60° D.90°
9.在![]() 的展开式中,含x的项的系数是( )
的展开式中,含x的项的系数是( )
A.55 B.-55 C.56 D.-56
|
A.![]()
B.![]()
C.![]()
D.![]()
11.an=![]() ,则
,则![]() 等于( )
等于( )
A.2![]() B.
B.![]() C.2-
C.2-![]() D.1-
D.1-![]()
12.设椭圆![]() ,右焦点F(c,0),方程
,右焦点F(c,0),方程![]() 的两个根分别为x1,x2,则点P(x1,x2)在( )
的两个根分别为x1,x2,则点P(x1,x2)在( )
A.圆![]() 内 B.圆
内 B.圆![]() 上
上
C.圆![]() 外 D.以上三种情况都有可能
外 D.以上三种情况都有可能
答题纸
一、选择题 (将正确答案的代号填入下表内)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
13.若函数![]() 的图象与函数
的图象与函数![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则![]() ________;
________;
14.若抛物线![]() 的焦点与椭圆
的焦点与椭圆![]() 的右焦点重合,则
的右焦点重合,则![]() 的值为 ;
的值为 ;
15.某考生从“××大学”所给的7个专业中选择3个作为自己的志愿,其中甲、乙两个专业不能同时兼报,则该考生有 种不同的填写志愿方法;
16.对于函数的这些性质:①奇函数;②偶函数;③增函数;④减函数;⑤周期性;函数![]() 具有的性质的序号是
.
具有的性质的序号是
.
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.)
17.(本小题满分10分)已知向量![]() ,记
,记![]()
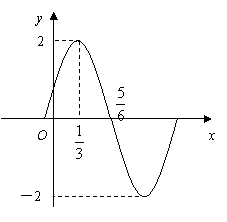
(1)求f(x)的值域及最小正周期;
(2)若![]() ,其中
,其中![]() ,求角
,求角![]()
18.(本小题满分12分)从4名男生和2名女生中任选3人参加演讲比赛.
(1)求所选3人都是男生的概率;
(2)求所选3人中至少有1名女生的概率.
19.(本小题满分12分)已知数列{an}前n项和为Sn(![]() ),且
),且![]()
![]()
![]() (1)求证:
(1)求证:![]() 是等差数列;
是等差数列;
(2)求an;
(3)若![]() ,求证:
,求证:![]()
20.(本小题满分12分)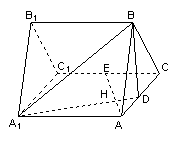 如图,正三棱柱
如图,正三棱柱![]() 的所有棱长都是
的所有棱长都是![]() ,
,![]() 是棱
是棱![]() 的中点,
的中点,![]() 是棱
是棱![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]()
(1)求证:![]() ;
;
(2)求二面角![]() 的大小(用反三角函数表示);
的大小(用反三角函数表示);
(3)求点![]() 到平面
到平面![]() 的距离。
的距离。
21.(本小题满分12分)设函数![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,
![]()
(1)当![]() 的解析式;
的解析式;
(2)若![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)是否存在m,使得![]() ?并说明理由.
?并说明理由.
22.(本小题满分12分)已知曲线C上任意一点M到点F(0,1)的距离比它到直线![]() 的距离小1.
的距离小1.
(1)求曲线C的方程;
(2)过点![]() 当△AOB的面积为
当△AOB的面积为![]() 时(O为坐标原点),求
时(O为坐标原点),求![]() 的值.
的值.
参考答案
DDDBC,CDCDA,B A
13.![]() 14.4 15.
14.4 15.![]() 16.①③
16.①③
17.(1)根据条件可知:
![]()
![]()
![]()
![]()
因为f(x)的定义域为![]()
∴f(x)的值域为![]() ,f(x)的最小正周期为
,f(x)的最小正周期为![]()
(2)![]()
所以,![]() ,又因为
,又因为![]() ,所以
,所以![]()
所以![]()
18.(1)所选3人都是男生的概率为 ![]()
(2)所选3人中至少有1名女生的概率为![]() ,或1-
,或1-![]()
19.(1)∵![]() ,∴
,∴![]() , 又∵
, 又∵![]() ∴
∴![]()
∴数列![]() 是等差数列,且
是等差数列,且![]()
(2)当![]() 时,
时,![]()
当n=1时,![]() 不成立. ∴
不成立. ∴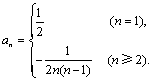
|
∴左边![]() 显然成立.
显然成立.
20.(1)证明:建立如图所示, ![]()
![]()
∵![]() ,
,![]()
∴![]() ,即AE⊥A1D, AE⊥BD ∴AE⊥面A1BD
,即AE⊥A1D, AE⊥BD ∴AE⊥面A1BD
(2)设面DA1B的法向量为![]()
由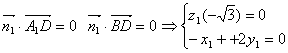 ∴取
∴取![]()
设面AA1B的法向量为 ![]()
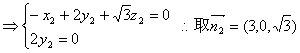 ,
,![]()
由图可知二面角D—BA1—A为锐角,∴它的大小为arcos![]()
(3)![]() ,平面A1BD的法向量取
,平面A1BD的法向量取![]()
则B1到平面A1BD的距离d=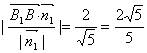
21.(1)设![]() ,
,![]()
![]() 为偶函数,
为偶函数,![]()
(2)![]() ,
,![]()
![]()
![]()
![]() 上为增 函数.
上为增 函数.
(3)当m<-2时,![]() 上是增函数,
上是增函数,![]()
![]() ,不合题意舍去.
,不合题意舍去.
当![]()
| x |
|
|
|
|
| + | 0 | — |
|
| 增 | 最大值 | 减 |
![]() 处取得最大值.
处取得最大值.![]()
![]() ,
,![]()
当m>0时,![]() 上单调递,
上单调递,![]() 上无最大值.
上无最大值.
![]() 上的最大值
上的最大值![]()
22. (1)![]() 的距离小于1,
的距离小于1,
∴点M在直线l的上方,点M到F(1,0)的距离与它到直线![]() 的距离相等
的距离相等 ![]() ,所以曲线C的方程为
,所以曲线C的方程为![]()
(2)当直线m的斜率不存在时,它与曲线C只有一个交点,不合题意,
设直线m的方程为![]() ,代入
,代入![]() (*)
(*)
![]() 与曲线C恒有两个不同的交点
与曲线C恒有两个不同的交点
设交点A,B的坐标分别为![]() ,则
,则![]()
![]()
点O到直线m的距离![]() ,
,
![]()
![]() ,
,
![]() (舍去)
(舍去)
![]()
当![]() 方程(*)的解为
方程(*)的解为![]()
若![]()
若![]()
当![]() 方程(☆)的解为
方程(☆)的解为![]()
若![]()
若![]()
所以,![]()