08高考数学第二轮复习函数练习
一、本章知识结构:
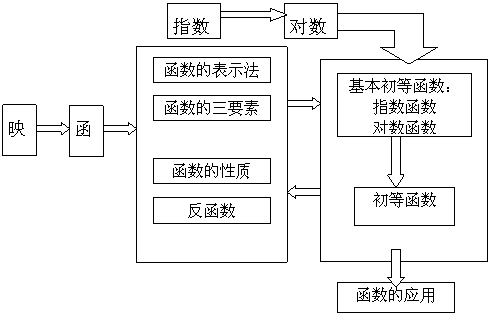
二、高考要求
(1)了解映射的概念,理解函数的概念.
(2)了解函数的单调性和奇偶性的概念,掌握判断一些简单函数的单调性和奇偶性的方法,并能利用函数的性质简化函数图像的绘制过程.
(3)了解反函数的概念及互为反函数的函数图像间关系,会求一些简单函数的反函数.
(4)理解分数指数的概念,掌握有理指数幂的运算性质.掌握指数函数的概念、图像和性质.
(5)理解对数的概念,掌握对数的运算性质.掌握对数函数的概念、图像和性质.
(6)能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题.
三、热点分析
函数是高考数学的重点内容之一,函数的观点和思想方法贯穿整个高中数学的全过程,包括解决几何问题。在近几年的高考试卷中,选择题、填空题、解答题三种题型中每年都有函数试题,而且常考常新。以基本函数为背景的应用题和综合题是高考命题的新趋势。
考试热点:①考查函数的表示法、定义域、值域、单调性、奇偶性、反函数和函数的图象。②函数与方程、不等式、数列是相互关联的概念,通过对实际问题的抽象分析,建立相应的函数模型并用来解决问题,是考试的热点。
③考查运用函数的思想来观察问题、分析问题和解决问题,渗透数形结合和分类讨论的基本数学思想。
四、复习建议
1. 认真落实本章的每个知识点,注意揭示概念的数学本质
①函数的表示方法除解析法外还有列表法、图象法,函数的实质是客观世界中量的变化的依存关系;
②中学数学中的“正、反比例函数,一次、二次函数,指数、对数函数,三角函数”称为基本初等函数,其余的函数的解析式都是由这些基本初等函数的解析式形成的. 要把基本初等函数的图象和性质联系起来,并且理解记忆;
③掌握函数单调性和奇偶性的一般判定方法,并能联系其相应的函数的图象特征,加强对函数单调性和奇偶性应用的训练;
④注意函数图象的变换:平移变换、伸缩变换、对称变换等;
⑤掌握复合函数的定义域、值域、单调性、奇偶性;
⑥理解掌握反函数的概念,会求反函数,弄清互为反函数的两个函数的定义域、值域、单调性的关联及其图像间的对称关系。
2. 以函数知识为依托,渗透基本数学思想和方法
①数形结合的思想,即要利用函数的图象解决问题;
②建模方法,要能在实际问题中引进变量,建立函数模型,进而提高解决应用题的能力,培养函数的应用意识。
3. 深刻理解函数的概念,加强与各章知识的横向联系
要与时俱进地认识本章内容的“双基”,准确、深刻地理解函数的概念,才能正确、灵活地加以运用,养成自觉地运用函数观点思考和处理问题的习惯;高考范围没有的内容例如指数不等式(方程)、对数不等式(方程)等不再作深入研究;导数可用来证明函数的单调性,求函数的最大值和最小值,并启发学生建构更加完整的函数知识结构。
所谓函数思想,实质上是将问题放到动态背景上去考虑,利用函数观点可以从较高的角度处理式、方程、不等式、数列、曲线等问题。
五、典型例题
【例1】
设![]() ,则
,则![]() = 1 。
= 1 。
解:由![]() =0,解得
=0,解得![]()
【例2】
已知函数![]() 和定义在R上的奇函数
和定义在R上的奇函数![]() ,当x>0时,
,当x>0时,![]() ,试求
,试求![]() 的反函数。
的反函数。
解: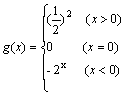
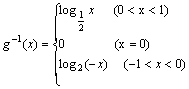
【例3】
已知函数![]() 是奇函数,又
是奇函数,又![]() ,求a、b、c的整数值。
,求a、b、c的整数值。
解:由![]() ,又由
,又由![]() ,从而可得a=b=1;c=0
,从而可得a=b=1;c=0
【例4】
⑴已知![]() ,求
,求![]()
⑵![]() 在
在![]() 上的最小值为
上的最小值为![]() ;试写出
;试写出![]() 的解析式。
的解析式。
解:⑴![]() ,
,![]() (
(![]() )
)
⑵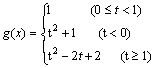
【例5】
已知函数![]() ,若
,若![]() 的最大值为n,求
的最大值为n,求![]() 的表达式。
的表达式。
解: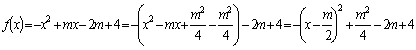
![]()

【例6】
设![]() 是R上的偶函数,且在区间
是R上的偶函数,且在区间![]() 上递增,若
上递增,若![]() 成立,求a的取值范围。
成立,求a的取值范围。
解:

![]()
![]()
故![]() 为所求。
为所求。
【例7】
比较![]() 的大小。
的大小。
解:作差比较大小:
![]()
![]()
![]()
![]()
![]()
![]()
当m > 1或0 < m < 1。都有u > 0
故![]() 。
。
【例8】
设![]() 。(1)证明
。(1)证明![]() 在
在![]() 上是增函数;(2)求
上是增函数;(2)求![]() 及其
及其
定义域
解:(1)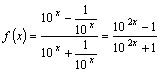
任取![]() ,且
,且![]()
![]()
![]() 是增函数,
是增函数,
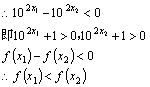
![]()
![]() 在
在![]() 上是增函数
上是增函数
(2)![]() ;定义域R,值域(-1, 1)
;定义域R,值域(-1, 1)
反解:![]()
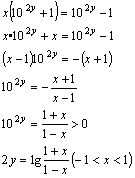
![]()
【例9】
定义在R上的函数![]() 满足:对任意实数
满足:对任意实数![]() ,总有
,总有![]() ,且当
,且当![]() 时,
时,![]() .
.
(1)试求![]() 的值;
的值;
(2)判断![]() 的单调性并证明你的结论;
的单调性并证明你的结论;
(3)设![]() ,若
,若![]() ,试确定
,试确定![]() 的取值范围.
的取值范围.
(4)试举出一个满足条件的函数![]() .
.
解:(1)在![]() 中,令
中,令![]() .得:
.得:
![]() .
.
因为![]() ,所以,
,所以,![]() .
.
(2)要判断![]() 的单调性,可任取
的单调性,可任取![]() ,且设
,且设![]() .
.
在已知条件![]() 中,若取
中,若取![]() ,则已知条件可化为:
,则已知条件可化为:![]() .
.
由于![]() ,所以
,所以![]() .
.
为比较![]() 的大小,只需考虑
的大小,只需考虑![]() 的正负即可.
的正负即可.
在![]() 中,令
中,令![]() ,
,![]() ,则得
,则得![]() .
.
∵ ![]() 时,
时,![]() ,
,
∴ 当![]() 时,
时,![]() .
.
又![]() ,所以,综上,可知,对于任意
,所以,综上,可知,对于任意![]() ,均有
,均有![]() .
.
∴ ![]() .
.
∴ 函数![]() 在R上单调递减.
在R上单调递减.
(3)首先利用![]() 的单调性,将有关函数值的不等式转化为不含
的单调性,将有关函数值的不等式转化为不含![]() 的式子.
的式子.
![]() ,
,
![]() ,即
,即![]() .
.
由![]() ,所以,直线
,所以,直线![]() 与圆面
与圆面![]() 无公共点.所以,
无公共点.所以,
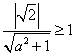 .
.
解得:![]() .
.
(4)如![]() .
.
六、专题练习
一、选择题
1.已知四个函数:①y=10x ②y=log0.1x ③y=lg(-x) ④y=0.1x,则图象关于原点成中心对称的是:(C)
A.仅为③和④ B.仅为①和④ C.仅为③和② D.仅为②和④
2.设f(x)=![]() (x+1),
(x+1),![]() (1)=
。(1)
(1)=
。(1)
3..已知,定义在实数集R上的函数f(x)满足:(1)f(-x)=
f(x);(2)f(4+x)=
f(x);若当
x![]()
[0,2]时,f(x)=![]() +1,则当x
+1,则当x![]() [-6,-4]时,f(x)等于 ( D )
[-6,-4]时,f(x)等于 ( D )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
![]()
4..已知f(x)=2
x+1,则![]() 的值是
(
A )
的值是
(
A )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)5
(D)5
5.已知函数f(x)=![]() +a且f(-1)=0,则
+a且f(-1)=0,则![]() 的值是 ( A
)
的值是 ( A
)
(A)0 (B)2 (C)1 (D)-1
6.函数![]() (x≥0)的反函数是
(
A )
(x≥0)的反函数是
(
A )
(A)![]() (B)y=
(B)y=![]()
(C)y![]() (C)y
(C)y![]()
7.函数f(x)的反函数为 g(x),则下面命题成立的是 ( A )
(A)若f(x)为奇函数且单调递增,则g(x)也是奇函数且单调递增。
(B)f(x)与g(x)的图像关于直线x+y=0对称。
(C)当f(x)是偶函数时,g(x)也是偶函数。
(D)f(x)与g(x)的图像与直线一定相交于一点。
8.若函数y=f(x)的图像经过点(0,1),则函数y=f(x+4)的反函数的图像必经过点 ( A )
(A)(1,-4) (B)(4,1) (C)(-4,1) (D)(1,4)
9.若函数![]() 在区间
在区间 ![]() 上是
上是
减函数,则实数a的取值范围是( B )
A.![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
10.将函数![]() 的图象向右平移2个单位后,再向上平移3个单位,所得函数
的图象向右平移2个单位后,再向上平移3个单位,所得函数
的解析式为( C )
A.![]() B.
B.
![]()
C.
![]() D.
D.
![]()
11.二次函数![]() 中,
中,![]() 且
且![]() ,对任意
,对任意![]() ,都有
,都有![]() ,设
,设![]() ,则( B )
,则( B )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 的大小关系不确定
的大小关系不确定
12.函数![]() 的值域为( B
)
的值域为( B
)
A.![]() B.
B.![]() C.
C.![]() D.R
D.R
13.已知![]() 在
在![]() 上是x的减函数,则a的值取范围是( B )
上是x的减函数,则a的值取范围是( B )
A.(0, 1) B.(1, 2) C.(0, 2) D.![]()
二、填空题
1.函数![]() 的定义域是 。(
的定义域是 。(![]() )
)
2.函数![]() 的单调递增区间是
的单调递增区间是 ![]()
3.函数![]() 的定义域是
的定义域是 ![]()
三、解答题
1.集合![]() ,B=
,B=![]() 。若
。若![]() ,求实数m的取值范围。
,求实数m的取值范围。
解:由![]() ,
,
由题设知上述方程在![]() 内必有解。
内必有解。
所以:⑴ 若在![]() 只有一个解,则
只有一个解,则![]()
⑵若在![]() 只有二个解,则
只有二个解,则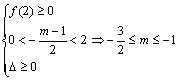
由⑴⑵知:![]()
2.设两个方程![]() 和
和![]() 有一公共根,问:
有一公共根,问:
⑴a与b之间有什么关系;⑵当![]() ,
,![]() 时,求
时,求![]() 的最大值与最小值。
的最大值与最小值。
解:⑴两方程相减得:![]() ,显然
,显然![]() ,否则两方程为同一方程。所以
,否则两方程为同一方程。所以![]() ,代入方程得:
,代入方程得:![]() 且
且![]()
⑵![]() ;
;
所当![]() 或
或![]() 时,
时,![]() ;
;
而当![]() 时,
时,![]() ,所以无最小值。
,所以无最小值。
3.当![]() 时,比较
时,比较![]() 与
与![]() 的大小。
的大小。
解:![]()
![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
4.x为何值时,不等式![]() 成立。
成立。
解:当![]() 时,
时,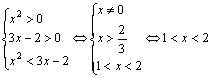
当![]() 时,
时,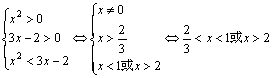
故![]() 时,
时,![]()
![]() 时,
时,![]() 为所求。
为所求。
5、已知函数![]()
(1)函数![]() 在区间(0,+
在区间(0,+![]() )上是增函数还是减函数?证明你的结论;
)上是增函数还是减函数?证明你的结论;
(2)若当![]() 时,
时,![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
解:(1)![]()
![]() .
.
因此函数![]() 在区间(0,+∞)上是减函数.
在区间(0,+∞)上是减函数.
(2)(方法1)当![]() 时,
时,![]() 恒成立,令
恒成立,令![]() 有
有![]()
又![]() 为正整数.
为正整数. ![]() 的最大值不大于3.……7′
的最大值不大于3.……7′
下面证明当![]()
![]() 恒成立.
恒成立.
即证当![]() 时,
时,![]() 恒成立.
恒成立.
令![]()
当![]()
![]() 取得最小值
取得最小值![]()
![]() 时,
时,![]() 恒成立.
恒成立.
因此正整数![]() 的最大值为3.
的最大值为3.
(2)(方法2)当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 恒成立.
恒成立.
即![]() 的最小值大于
的最小值大于![]()
![]()
![]() 上连续递增,
上连续递增,
又![]()
![]() 存在唯一实根
存在唯一实根![]() ,且满足:
,且满足:![]()
由![]() 知:
知:
![]() 的最小值为
的最小值为![]()
因此正整数![]() 的最大值为3.
的最大值为3.
第2讲
一、典型例题
【例1】 关于x的不等式2·32x–3x+a2–a–3>0,当0≤x≤1时恒成立,则实数a的取值范围为 .
解:设t=3x,则t∈[1,3],原不等式可化为a2–a–3>–2t2+t,t∈[1,3].
等价于a2–a–3大于f(t)=–2t2+t在[1,3]上的最大值.
答案:(–∞,–1)∪(2,+∞)
【例2】
设![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,而当
对称,而当![]() 时,
时,![]() (c为常数)。
(c为常数)。
(1)求![]() 的表达式;
的表达式;
(2)对于任意![]() ,
,![]() 且
且![]() ,求证:
,求证:![]() ;
;
(3)对于任意![]() ,
,![]() 且
且![]() ,求证:
,求证:![]() 1.
1.
解:(1)设g(x)上点![]() 与f(x)上点P(x,y)对应,
与f(x)上点P(x,y)对应,
∴![]() ;∵
;∵![]() 在g(x)图象上
在g(x)图象上
∴![]()
∵g(x)定义域为x∈[2,3],而f(x)的图象与g(x)的图象关于直线x=1对称,
所以,上述解析式是f(x)在[–1,0]上的解析式
∵f(x)是定义在[–1,1]上的奇函数,∴f(0)=0,∴c=–4
所以,当x∈[0,1]时,–x∈[–1,0],f(x)=–f(–x)=–![]()
所以![]()
(2)当x∈[0,1]时,![]()
∵![]() ,∴
,∴![]() ,所以
,所以![]()
(3)∵![]() ,∴
,∴![]()
∴![]() ,∴
,∴![]()
即![]()
【例3】
已知函数f(x)=![]() (a>0, a≠1)
(a>0, a≠1)
(1) 求反函数f![]() (x),并求出其定义域。
(x),并求出其定义域。
(2) 设P(n)=![]() ),如果P(n)<
),如果P(n)<![]() (n∈N),求a的取值范围。
(n∈N),求a的取值范围。
解:(1) 设y= f(x)=log![]()
∴ay=x+![]()
两端平方整理得:a2y-2xay+2=0Þx=![]()
∴![]() ∵a>1时,f(x)=
∵a>1时,f(x)=![]() 值域为
值域为![]()
0<a<1时,f(x)的值域为![]()
∴ f-1 (x)的定义域为:a>1时,x∈![]() 0<a<1时,x∈
0<a<1时,x∈![]()
(2) P(n)=![]()
由![]()
即an+a-n-(3n-3-n)=![]()
∵(3a)n>0 ∴(an-3n)[(3a)n-1]<0Þ![]() <a<3;
<a<3;
又∵n∈N,∴n+![]() >
>![]() Þa>1
Þa>1
即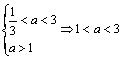
【例4】
设函数f(x)的定义域关于原点对称,且满足①![]() ②存在正常数a,使f(a) = 1,求证:(1)f(x)为奇函数;(2)f(x)为周期函数,且一个周期为4a。
②存在正常数a,使f(a) = 1,求证:(1)f(x)为奇函数;(2)f(x)为周期函数,且一个周期为4a。
证明:(1)令x =x1 - x2
则f( - x) = f ( x2
- x1)=![]()
= -f (x1 -x2 )= -f (x),∴f (x)为奇函数。
(2)∵f( x+a ) = f[x - ( -a ) ]=![]()
∴f (x+2a )=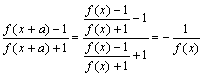
∴f ( x+4a)=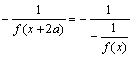 =f (x)
=f (x)
∴f (x)是以4a为周期的周期函数。
【例5】
已知函数f(x)=logm![]()
(1)若f(x)的定义域为![]() ,(β>α>0),判断f(x)在定义域上的增减性,并加以说明;
,(β>α>0),判断f(x)在定义域上的增减性,并加以说明;
(2)当0<m<1时,使f(x)的值域为![]() 的定义域区间为
的定义域区间为![]()
(β>α>0)是否存在?请说明理由.
解:(1)![]() x<–3或x>3.
x<–3或x>3.
∵f(x)定义域为![]() ,∴α>3
,∴α>3
设β≥x1>x2≥α,有![]()
当0<m<1时,f(x)为减函数,当m>1时,f(x)为增函数.
(2)若f(x)在![]() 上的值域为
上的值域为![]()
∵0<m<1, f(x)为减函数.
∴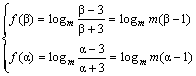
即![]()
即α,β为方程mx2+(2m–1)x–3(m–1)=0的大于3的两个根
∴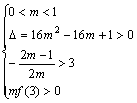 ∴0<m<
∴0<m<![]()
故当0<m<![]() 时,满足题意条件的m存在.
时,满足题意条件的m存在.
【例6】 已知函数f(x)=x2–(m+1)x+m(m∈R)
(1)若tanA,tanB是方程f(x)+4=0的两个实根,A、B是锐角三角形ABC的两个内角.求证:m≥5;
(2)对任意实数α,恒有f(2+cosα)≤0,证明m≥3;
(3)在(2)的条件下,若函数f(sinα)的最大值是8,求m.
解: (1)证明:f(x)+4=0即x2–(m+1)x+m+4=0.依题意:
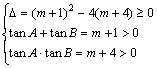 又A、B锐角为三角形内两内角
又A、B锐角为三角形内两内角
∴![]() <A+B<π
<A+B<π
∴tan(A+B)<0,即![]()
∴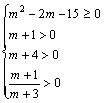 ∴m≥5
∴m≥5
(2)证明:∵f(x)=(x–1)(x–m)
又–1≤cosα≤1,∴1≤2+cosα≤3,恒有f(2+cosα)≤0
即1≤x≤3时,恒有f(x)≤0即(x–1)(x–m)≤0
∴m≥x但xmax=3,∴m≥xmax=3
(3)解:∵f(sinα)=sin2α–(m+1)sinα+m=![]()
且![]() ≥2,∴当sinα=–1时,f(sinα)有最大值8.
≥2,∴当sinα=–1时,f(sinα)有最大值8.
即1+(m+1)+m=8,∴m=3
【例7】
已知函数![]() 的定义域为实数集。(1)求实数m的所有允许值组成的集合M;(2)求证:对所有
的定义域为实数集。(1)求实数m的所有允许值组成的集合M;(2)求证:对所有![]() ,恒有
,恒有 ![]() 。
。
证明(1)∵![]() 的定义域为实数集
的定义域为实数集
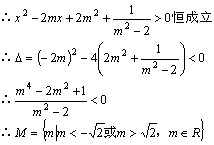
(2)令![]()
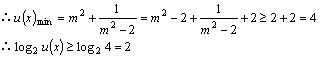
【例8】
设![]() =
=![]() ,(a>0,a≠1),求证:(1)过函数y=f(x)图象上任意两点直线的斜率恒大于0;(2)f(3)>3。
,(a>0,a≠1),求证:(1)过函数y=f(x)图象上任意两点直线的斜率恒大于0;(2)f(3)>3。
解:(1)令t=![]() ,则x=
,则x=![]() ,f(x)=
,f(x)= ![]() (t∈R)
(t∈R)
∴f(x)= ![]() (x∈R)
(x∈R)
设![]() ,f(
,f(![]() )-f(
)-f(![]() )=
)=![]()
(1)a>1时,…,f(![]() )<f(
)<f(![]() ),∴f(x)在(-∞,+∞)上单调递增
),∴f(x)在(-∞,+∞)上单调递增
(2)0<a<1时,…,f(![]() )<f(
)<f(![]() ),∴f(x)在(-∞,+∞)上单调递增
),∴f(x)在(-∞,+∞)上单调递增
∴![]() <
<![]() 时,恒有f(
时,恒有f(![]() )<f(
)<f(![]() ),∴K=
),∴K=![]() >0
>0
(2)f(3)=![]()
∵a>0,a≠1 ∴![]() ∴上述不等式不能取等号,∴f(x)>3
∴上述不等式不能取等号,∴f(x)>3
【例9】
已知函数f(x)=lg(![]() 的定义域为(0,+∞),问是否存在这样的a,b,使f(x)恰在(1,+∞)上取正值,且f(3)=lg4,若存在,求出a,b的值,若不存在,说明理由。
的定义域为(0,+∞),问是否存在这样的a,b,使f(x)恰在(1,+∞)上取正值,且f(3)=lg4,若存在,求出a,b的值,若不存在,说明理由。
解:由![]() ,得
,得![]() ,∵a>1>b>0,∴
,∵a>1>b>0,∴![]() >1,∴x>log
>1,∴x>log![]()
又f(x)定义域为(0,+∞),∴log![]() =0,K=1,∴f(x)=lg
=0,K=1,∴f(x)=lg![]()
设0<![]() ,
,![]() ,∵a>1>b>0,∴a
,∵a>1>b>0,∴a![]() < a
< a![]() ,-b
,-b![]() < b
< b![]()
∴0< a![]() -b
-b![]() < a
< a![]() - b
- b![]() ,∴0<
,∴0<![]() <1,∴lg
<1,∴lg![]() <0
<0
∴![]() ,∴f(x)在(0,+∞)上是增函数
,∴f(x)在(0,+∞)上是增函数
∴x![]() (1,+∞)时,必有f(x)>f(1)=lg(a-b)
(1,+∞)时,必有f(x)>f(1)=lg(a-b)
∵f(x)在(1,+∞)上取正值,∴lg(a-b)=0 a-b=1 (1)
又f(3)=lg4 ∴lg![]() =lg4,
=lg4,![]() =4 (2)
=4 (2)
解(1)(2)得:![]() ,b=
,b=![]() ,即有在
,即有在![]() ,b=
,b=![]() 满足条件
满足条件
【例10】 设二次函数f(x)= ax2 +bx+c (a>0且b≠0)。
(1) 已知f(0)=f(1)=f(-1)=1,试求f(x)的解析式和f(x)的最小值;
(2) 已知f(x)的对称轴方程是x=1,当f(x)的图象在x轴上截得的弦长不小于2时,试求a, b, c满足的条件;
(3) 已知b<a, f(0)![]() 1, f(-1)
1, f(-1)![]() 1, f(1)
1, f(1)![]() 1,当x
1,当x![]() 1时,证明:f(x)
1时,证明:f(x)![]()
![]()
解:(1)由f(0)=f(1)=f(-1)知c=1,a+b+c=1,a-b+c=1
∴(a+b+c)2=(a-b+c)2即4(a+c)b=0
∵b≠0 ∴a+c=0,即:a=-c
又∵a>0 ∴a=1 c=-1 此时b=+1 ∴f(x)=x2 + x-1
于是 f(x)=(x + ![]() )2
)2![]() ∴[f(x)]
∴[f(x)]![]()
(2)依题意![]() 即b=-2a,∵a>0且b≠0 ∴b<0
即b=-2a,∵a>0且b≠0 ∴b<0
令f(x)=0的两根为x1,x2,则函数y=f(x)的图象与x轴的两个交点为(x1,0),(x2,0)
且![]() ,满足题设的充要条件是
,满足题设的充要条件是
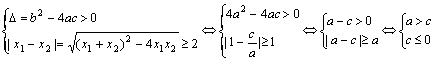
∴a>0 c![]() 0 b<0且b=-2a为所求
0 b<0且b=-2a为所求
(3)方法1:
∵2b=(a+b+c)-(a-b+c)<a+b+c+a-b+c<2 ∴b![]() 1 又b
1 又b![]() a ∴
a ∴![]()
![]() 1
1
又c=f(0)![]() 1 又f(
1 又f(![]()
而f(x)所示开口向上的抛物线且x<1,则f(x)的最大值应在x=1或x=-1或x=-![]() 时取到,因f(-1)<1,
f(1)
时取到,因f(-1)<1,
f(1)![]() 1, f(-
1, f(-![]() )
)![]()
![]() 故f(x)
故f(x)![]()
![]() 得证。
得证。
方法2:
令f(x)=uf(1)+vf(-1)+(1-u-v)f(0) 则f(x)=(a+b+c)u+(a-b+c)v+(1-u-v)c
ax2 +bx+c=a(u+v)+b(u-v)+c
∴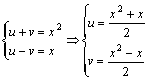
∴f(x)=![]()
而f(1)
![]() 1, f(-1)
1, f(-1)![]() 1, f(0)
1, f(0)![]() 1
1
∴![]() <
<![]() x∈[-1, 1]
x∈[-1, 1]
=x·![]() =
=![]() =
=![]()
综上,当f(0)![]() 1, f (-1)
1, f (-1)![]() 1, f(-1)
1, f(-1)![]() 1, x
1, x![]() 1时,f(x)
1时,f(x)![]()
解法3:我们可以把![]() ,
,![]() 和
和![]() 当成两个独立条件,先用
当成两个独立条件,先用![]() 和
和![]() 来表示
来表示![]() .
.
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
∴ 当![]() 时,
时,![]() ,所以,根据绝对值不等式的性质可得:
,所以,根据绝对值不等式的性质可得:
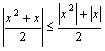 ,
,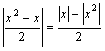 ,
,![]()
∴ ![]()
![]()
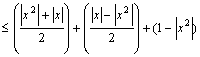
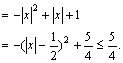
综上,问题获证.
二、专题练习
一、选择题
1.(2005年春考·北京卷·理2)函数y=log2x的图象是 ( A )

 2.(2005年春考·北京卷·文2)函数
2.(2005年春考·北京卷·文2)函数![]() ( B )
( B )
3. (2005年春考·上海卷16)设函数![]() 的定义域为
的定义域为![]() ,有下列三个命题:
,有下列三个命题:
(1)若存在常数![]() ,使得对任意
,使得对任意![]() ,有
,有![]() ,则
,则![]() 是函数
是函数![]() 的最大值;
的最大值;
(2)若存在![]() ,使得对任意
,使得对任意![]() ,且
,且![]() ,有
,有![]() ,则
,则![]() 是函数
是函数![]()
的最大值;
(3)若存在![]() ,使得对任意
,使得对任意![]() ,有
,有![]() ,则
,则![]() 是函数
是函数![]() 的最大值.
的最大值.
这些命题中,真命题的个数是 ( C )
A.0个 B.1个 C.2个 D.3个
4.(2005年高考·上海卷·理13文13)若函数![]() ,则该函数在
,则该函数在![]() 上是 ( A )
上是 ( A )
A.单调递减无最小值 B.单调递减有最小值
C.单调递增无最大值 D.单调递增有最大值
5.(2005年高考·上海卷·理16)设定义域为R的函数![]() ,则关于
,则关于![]() 的方程
的方程![]() 有7个不同实数解的充要条件是 ( C )
有7个不同实数解的充要条件是 ( C )
A.![]() 且
且![]() B.
B.![]() 且
且![]() C.
C.![]() 且
且![]() D.
D.![]() 且
且![]()
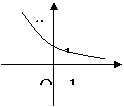 6.(2005年高考·福建卷·理5文6)函数
6.(2005年高考·福建卷·理5文6)函数![]() 的图象如图,其中a、b为常数,则下列结论正确的是 ( D )
的图象如图,其中a、b为常数,则下列结论正确的是 ( D )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7.(2005年高考·福建卷·理12)![]() 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且![]() 则方程
则方程![]() =0在区间(0,6)内解的个数的最小值是 ( D )
=0在区间(0,6)内解的个数的最小值是 ( D )
A.2 B.3 C.4 D.5
8.(2005年高考·福建卷·文12)![]() 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且![]() ,则方程
,则方程![]() =0在区间(0,6)内解的个数的最小值是 ( B )
=0在区间(0,6)内解的个数的最小值是 ( B )
A.5 B.4 C.3 D.2
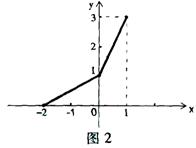 9.(2005年高考·广东卷9)在同一平面直角坐标系中,函数
9.(2005年高考·广东卷9)在同一平面直角坐标系中,函数![]() 和
和![]() 的图象关于直线
的图象关于直线![]() 对称. 现将
对称. 现将![]() 的图象沿
的图象沿![]() 轴向左平移2个单位, 再沿
轴向左平移2个单位, 再沿![]() 轴向上平移1个单位,所得的图象是由两条线段组成的折线(如图2所示),则函数
轴向上平移1个单位,所得的图象是由两条线段组成的折线(如图2所示),则函数![]() 的表达式为( A )
的表达式为( A )
A.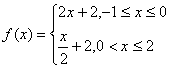
B.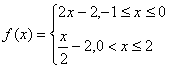
C.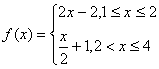 D.
D.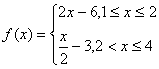
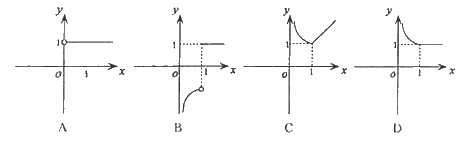
10.(2005年高考·湖北卷·理4文4)函数![]() 的图象大致是 ( D )
的图象大致是 ( D )
11.(2005年高考·湖北卷·理6文7)在![]() 这四个函数中,当
这四个函数中,当![]() 时,使
时,使![]() 恒成立的函数的个数是 ( B )
恒成立的函数的个数是 ( B )
A.0 B.1 C.2 D.3
12.(2005年高考·湖南卷·理2)函数f(x)=![]() 的定义域是 ( A)
的定义域是 ( A)
A.![]() -∞,0] B.[0,+∞
-∞,0] B.[0,+∞![]() C.(-∞,0) D.(-∞,+∞)
C.(-∞,0) D.(-∞,+∞)
13.(2005年高考·湖南卷·文3)函数f(x)=![]() 的定义域是 ( A)
的定义域是 ( A)
A.![]() -∞,0] B.[0,+∞
-∞,0] B.[0,+∞![]() C.(-∞,0) D.(-∞,+∞)
C.(-∞,0) D.(-∞,+∞)
14.(2005年高考·湖南卷·文10)某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为L1=5.06x-0.15 x 2和L2=2 x,其中x为销售量(单位:辆).若该公司在这两地共销售15辆车,则能获得的最大利润为 ( B )
A.45.606 B.45.6 C.45.56 D.45.51
15.(2005年高考·辽宁卷5)函数![]() 的反函数是 ( C )
的反函数是 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.(2005年高考·辽宁卷6)若![]() ,则
,则![]() 的取值范围是 ( C )
的取值范围是 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
17.(2005年高考·辽宁卷7)在R上定义运算![]() 若不等式
若不等式![]() 对任意实数
对任意实数![]() 成立,
则 ( C )
成立,
则 ( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
18.(2005年高考·辽宁卷10)已知![]() 是定义在R上的单调函数,实数
是定义在R上的单调函数,实数![]() ,
,![]()
![]() ,若
,若![]() ,则 ( A )
,则 ( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
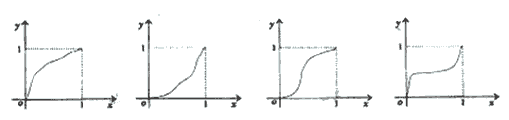
19.(2005年高考·辽宁卷12)一给定函数![]() 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意![]() ,由关系式
,由关系式![]() 得到的数列
得到的数列![]() 满足
满足![]() ,则该函数的图象是( A )
,则该函数的图象是( A )
 A
B
C D
A
B
C D
20.(2005年高考·江西卷·理10文10)已知实数a, b满足等式![]() 下列五个关系式
下列五个关系式
①0<b<a ②a<b<0 ③0<a<b ④b<a<0 ⑤a=b
其中不可能成立的关系式有 ( B )
A.1个 B.2个 C.3个 D.4个
21.(2005年高考·江西卷·文4)函数![]() 的定义域为 ( A )
的定义域为 ( A )
A.(1,2)∪(2,3) B.![]()
C.(1,3) D.[1,3]
22.(2005年高考·重庆卷·理3文3)若函数![]() 是定义在R上的偶函数,在
是定义在R上的偶函数,在![]() 上是减函数,且
上是减函数,且![]() ,则使得
,则使得![]() 的x的取值范围是 ( D )
的x的取值范围是 ( D )
A.![]() B.
B.![]() C.
C.![]() D.(-2,2)
D.(-2,2)
23.(2005年高考·重庆卷·文5)不等式组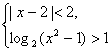 的解集为 (
C )
的解集为 (
C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
24.(2005年高考·江苏卷2)函数![]() 的反函数的解析表达式为 (
A )
的反函数的解析表达式为 (
A )
A.![]() B.
B.
![]()
C.![]() D.
D.
![]()
25.(2005年高考·浙江卷·理3)设f(x)=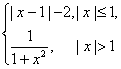 ,则f[f(
,则f[f(![]() )]= (
B )
)]= (
B )
A.![]() B.
B.![]() C.-
C.-![]() D.
D.
![]()
26.(2005年高考·浙江卷·文4)设f(x)=x-1-x,则f[f(![]() )]= ( D
)
)]= ( D
)
A.-![]() B.0 C.
B.0 C.![]() D.
1
D.
1
27.(2005年高考·浙江卷·文9)函数y=ax2+1的图象与直线y=x相切,则a= ( B )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
28.(2005年高考·山东卷·理2文3)函数![]() 的反函数图像大致是( B)
的反函数图像大致是( B)
A. B. C. D.
29.(2005年高考·山东卷·理11)![]() ,下列不等式一定成立的是 ( A )
,下列不等式一定成立的是 ( A )
A.![]() B.
B.![]()
C.![]()
![]()
D.![]()
![]()
30.(2005年高考·山东卷·文2)下列大小关系正确的是 ( C)
A.![]() ;
B.
;
B.![]() ;
;
C.![]() ; D.
; D.![]()
31.(2005年高考·天津卷·文2)已知![]() ,则 (
A )
,则 (
A )
A. 2b>2a>2c B.2a>2b>2c C.2c>2b>2a D.2c>2a>2b
32.(2005年高考·天津卷·理9)设![]() 是函数
是函数![]() 的反函数,则使
的反函数,则使![]() 成立的x的取值范围为 ( A )
成立的x的取值范围为 ( A )
A.![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
33.(2005年高考·天津卷·理10)若函数![]() 在区间
在区间![]() 内单调递增,则a的取值范围是 ( B )
内单调递增,则a的取值范围是 ( B )
A.![]() B.
B.
![]() C.
C.![]() D.
D.![]()
34.(2005年高考·天津卷·文9)若函数![]() 在区间
在区间![]() 内恒有f(x)>0,则f(x)的单调递增区间为 ( D)
内恒有f(x)>0,则f(x)的单调递增区间为 ( D)
A.![]() B.
B.![]() C.(0,¥) D.
C.(0,¥) D.![]()
35.(2005年高考·天津卷·文10)设f(x)是定义在R上以6为周期的函数,f(x)在(0,3)内单调递增,且yf(x)的图象关于直线x3对称,则下面正确的结论是 ( B)
A. f(1.5)<f(3.5)<f(6.5) B. f(3.5)<f(1.5)<f(6.5)
C. f(6.5)<f(3.5)<f(1.5) D. f(3.5)<f(6.5)<f(1.5)
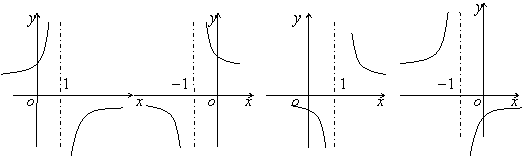
36.(2005年高考·全国卷Ⅰ·理7)设![]() ,二次函数
,二次函数![]() 的图象下列之一:则a的值为 ( C )
的图象下列之一:则a的值为 ( C )
 A.1 B.-1 C.
A.1 B.-1 C.![]() D.
D.![]()
37.(2005年高考·全国卷Ⅰ·理8文8)设![]() ,函数
,函数![]() ,则使
,则使![]() 取值范围是( B )
取值范围是( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
38.(2005年高考·全国卷Ⅰ·文7)![]() 的反函数是 ( C )
的反函数是 ( C )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
39.(2005年高考·全国卷II·理3)函数![]() 的反函数是 ( B )
的反函数是 ( B )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
40.(2005年高考·全国卷II·文3)函数![]() 的反函数是 ( B )
的反函数是 ( B )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
41.(2005年高考·全国卷Ⅲ·理6文6)若![]() ,则 ( C )
,则 ( C )
A.a<b<c B.c<b<a C.c<a<b D.b<a<c
42.(2005年高考·全国卷Ⅲ·文5)设![]() ,则 ( A )
,则 ( A )
A.-2<x<-1 B.-3<x<-2 C.-1<x<0 D.0<x<1
二、填空题
1.(2005年春考·北京卷·理14)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,则实数
,则实数![]() 的取值范围是__________;若关于
的取值范围是__________;若关于![]() 的不等式
的不等式![]() 的解集不是空集,则实数
的解集不是空集,则实数![]() 的取值范围是__________.
的取值范围是__________.![]() 文14仅前一个空
文14仅前一个空
2. (2005年春考·上海卷1)方程![]() 的解集是
.
的解集是
. ![]()
3. (2005年春考·上海卷4)函数![]()
![]() 的反函数
的反函数![]() .
. ![]()
4.(2005年高考·北京卷·理13文13)对于函数![]() 定义域中任意的
定义域中任意的![]() ,有如下结论:
,有如下结论:
①![]() ; ②
; ②![]() ;
;
③![]() ④
④![]()
当![]() 时,上述结论中正确结论的序号是
.②③
时,上述结论中正确结论的序号是
.②③
5.(2005年高考·北京卷·文11)函数![]() 的定义域为
.
的定义域为
. ![]()
6.(2005年高考·上海卷·理1文1)函数![]() 的反函数
的反函数![]() =__________.
=__________.![]()
7.(2005年高考·上海卷·理2文2)方程![]() 的解是__________. x=0
的解是__________. x=0
8.(2005年高考·福建卷·理16文16)把下面不完整的命题补充完整,并使之成为真命题:
若函数![]() 的图象与
的图象与![]() 的图象关于
对称,则函数
的图象关于
对称,则函数![]() =
=
。(注:填上你认为可以成为真命题的一件情形即可,不必考虑所有可能的情形). 如 ①x轴,-3-log2x ②y轴,3+log2(-x) ③原点,-3-log2(x) ④直线y=x, 2x-3
9.(2005年高考·广东卷11)函数![]() 的定义域是
. {xx<0}
的定义域是
. {xx<0}
10.(2005年高考·湖北卷·文13)函数![]() 的定义域是
.
的定义域是
. ![]()
11.(2005年高考·湖南卷·理14文14)设函数f(x)的图象关于点(1,2)对称,且存在反函数f-1(x),f (4)=0,则f-1(4)= .-2
12.(2005年高考·江西卷·理13文13)若函数![]() 是奇函数,则a=
.
是奇函数,则a=
. ![]()
13.(2005年高考·江苏卷13)命题“若![]() ,则
,则![]() ”的否命题为_____________________。若
”的否命题为_____________________。若![]() ,则
,则![]()
14.(2005年高考·江苏卷15)函数![]() 的定义域为_____________________。
的定义域为_____________________。![]()
15.(2005年高考·江苏卷16)若![]() ,
,![]() ,则k =______________。-1
,则k =______________。-1
16.(2005年高考·江苏卷17)已知a,b为常数,若![]() ,
,![]() ,则
,则![]() _________。2
_________。2
17.(2005年高考·浙江卷·理11文11)函数y=![]() (x∈R,且x≠-2)的反函数是_________.
(x∈R,且x≠-2)的反函数是_________.![]()
18.(2005年高考·天津卷·理16)设f(x)是定义在R上的奇函数,且y=f (x)的图象关于直线![]() 对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________. 0
对称,则f (1)+ f (2)+ f (3)+ f (4)+ f
(5)=________________. 0
19.(2005年高考·天津卷·文15)设函数![]() ,则函数
,则函数![]() 的定义域为__________
的定义域为__________![]() (2,1)È(1,2)
(2,1)È(1,2)
21.(2005年高考·全国卷Ⅰ·理13文13)若正整数m满足![]() 155
155
三、解答题
1.(本小题满分12分)(2005年春考·北京卷·理15)
设函数![]() 的定义域为集合M,函数
的定义域为集合M,函数![]() 的定义域为集合N.求:
的定义域为集合N.求:
(1)集合M,N;
(2)集合![]() ,
,![]() .
.
本小题主要考查集合的基本知识,考查逻辑思维能力和运算能力.满分12分.
解:(Ⅰ)![]()
![]()
(Ⅱ)![]()
![]() .
.
2.(本小题满分12分)(2005年春考·北京卷·文15)
记函数![]() 的定义域为集合M,函数
的定义域为集合M,函数![]() 的定义域为集合N.求:
的定义域为集合N.求:
(1)集合M,N;
(2)集合![]() ,
,![]() .
.
本小题主要考查集合的基本知识,考查逻辑思维能力和运算能力.满分12分.
解:(Ⅰ)![]()
![]()
(Ⅱ)![]()
![]() .
.
3.(本小题满分14分)(2005年高考·广东卷19)
设函数![]() ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有![]() (Ⅰ)试判断函数
(Ⅰ)试判断函数![]() 的奇偶性;
的奇偶性;
(Ⅱ)试求方程![]() 在闭区间[-2005,2005]上的根的个数,并证明你的结论.
在闭区间[-2005,2005]上的根的个数,并证明你的结论.
解: (I) 由于在闭区间[0,7]上,只有![]() ,故
,故![]() .若
.若![]() 是奇函数,则
是奇函数,则![]() ,矛盾.所以,
,矛盾.所以,![]() 不是奇函数.
不是奇函数.
由![]()
![]() , 从而知函数
, 从而知函数![]() 是以
是以![]() 为周期的函数.
为周期的函数.
若![]() 是偶函数,则
是偶函数,则![]() .又
.又![]() ,从而
,从而![]() .
.
由于对任意的![]() (3,7]上,
(3,7]上,![]() ,又函数
,又函数![]() 的图象的关于
的图象的关于![]() 对称,所以对区间[7,11)上的任意
对称,所以对区间[7,11)上的任意![]() 均有
均有![]() .所以,
.所以,![]() ,这与前面的结论矛盾.
,这与前面的结论矛盾.
所以,函数![]() 是非奇非偶函数.
是非奇非偶函数.
(II) 由第(I)小题的解答,我们知道![]() 在区间(0,10)有且只有两个解,并且
在区间(0,10)有且只有两个解,并且![]() .由于函数
.由于函数![]() 是以
是以![]() 为周期的函数,故
为周期的函数,故![]() .所以在区间[-2000,2000]上,方程
.所以在区间[-2000,2000]上,方程![]() 共有
共有![]() 个解.
个解.
在区间[2000,2010]上,方程![]() 有且只有两个解.因为
有且只有两个解.因为
![]() ,
,
所以,在区间[2000,2005]上,方程![]() 有且只有两个解.
有且只有两个解.
在区间[-2010,-2000]上,方程![]() 有且只有两个解.因为
有且只有两个解.因为
![]() ,
,
所以,在区间[-2005,-2000]上,方程![]() 无解.
无解.
综上所述,方程![]() 在[-2005,2005]上共有802个解.
在[-2005,2005]上共有802个解.
(2005年高考·浙江卷·理16)已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2=2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-x-1.
4.(2005年高考·浙江卷·理16文20)已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2+2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-x-1;
(Ⅲ)(文20)若h(x)=g(x)-![]() f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)设函数![]() 的图象上任意一点
的图象上任意一点![]() 关于原点的对称点为
关于原点的对称点为![]() ,则
,则
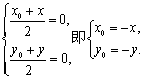
∵点![]() 在函数
在函数![]() 的图象上
的图象上
∴![]()
(Ⅱ)由![]()
当![]() 时,
时,![]() ,此时不等式无解
,此时不等式无解![]()
当![]() 时,
时,![]() ,解得
,解得![]()
![]()
因此,原不等式的解集为![]()
![]()
(Ⅲ)(文20)![]()
①![]()
![]()
②![]()
ⅰ)![]()
ⅱ)![]()
![]()
5.(本小题满分12分)(2005年高考·全国卷Ⅰ·文19)
已知二次函数![]() 的二次项系数为a,且不等式
的二次项系数为a,且不等式![]() 的解集为(1,3).
的解集为(1,3).
(1)若方程![]() 有两个相等的根,求
有两个相等的根,求![]() 的解析式;
的解析式;
(2)若![]() 的最大值为正数,求a的取值范围.
的最大值为正数,求a的取值范围.
本小题主要考查二次函数、方程的根与系数关系,考查运用数学知识解决问题的能力.满分12分.
解:(Ⅰ)![]()
![]()
![]() ①
①
由方程![]() ②
②
因为方程②有两个相等的根,所以![]() ,
,
即 ![]()
由于![]() 代入①得
代入①得![]() 的解析式
的解析式
![]()
(Ⅱ)由![]()
及![]()
由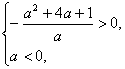 解得
解得 ![]()
故当![]() 的最大值为正数时,实数a的取值范围是
的最大值为正数时,实数a的取值范围是![]()
6.(本小题满分12分)(2005年高考·全国卷II·理17)
设函数![]() 的取值范围.
的取值范围.
本小题主要考查指数函数的性质、不等式性质和解法,考查分析问题的能力和计算能力,满分12分
解:由于![]() 是增函数,
是增函数,![]() 等价于
等价于![]() ①
①
(1) 当![]() 时,
时,![]() ,
,![]() ①式恒成立。
①式恒成立。
(2) 当![]() 时,
时,![]() ,①式化为
,①式化为![]() ,即
,即![]()
(3) 当![]() 时,
时,![]() ,①式无解
,①式无解
综上![]() 的取值范围是
的取值范围是![]()