08高考数学第二轮复习平面向量
一、本章知识结构:

二、高考要求
1、理解向量的概念,掌握向量的几何表示,了解共线向量的概念。2、掌握向量的加法和减法的运算法则及运算律。3、掌握实数与向量的积的运算法则及运算律,理解两个向量共线的充要条件。4、了解平面向量基本定理,理解平面向量的坐标的概念,掌握平面向量的坐标运算。5、掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的条件。6、掌握线段的定比分点和中点坐标公式,并且能熟练运用;掌握平移公式。7、掌握正、余弦定理,并能初步运用它们解斜三角形。8、通过解三角形的应用的教学,继续提高运用所学知识解决实际问题的能力。
三、热点分析
对本章内容的考查主要分以下三类:
1.以选择、填空题型考查本章的基本概念和性质.此类题一般难度不大,用以解决有关长度、夹角、垂直、判断多边形形状等问题.
2.以解答题考查圆锥曲线中的典型问题.此类题综合性比较强,难度大,以解析几何中的常规题为主.
3.向量在空间中的应用(在B类教材中).在空间坐标系下,通过向量的坐标的表示,运用计算的方法研究三维空间几何图形的性质.
在复习过程中,抓住源于课本,高于课本的指导方针.本章考题大多数是课本的变式题,即源于课本.因此,掌握双基、精通课本是本章关键.分析近几年来的高考试题,有关平面向量部分突出考查了向量的基本运算。对于和解析几何相关的线段的定比分点和平移等交叉内容,作为学习解析几何的基本工具,在相关内容中会进行考查。本章的另一部分是解斜三角形,它是考查的重点。总而言之,平面向量这一章的学习应立足基础,强化运算,重视应用。考查的重点是基础知识和基本技能。
四、复习建议
由于本章知识分向量与解斜三角形两部分,所以应用本章知识解决的问题也分为两类:一类是根据向量的概念、定理、法则、公式对向量进行运算,并能运用向量知识解决平面几何中的一些计算和证明问题;另一类是运用正、余弦定理正确地解斜三角形,并能应用解斜三角形知识解决测量不可到达的两点间的距离问题。
在解决关于向量问题时,一是要善于运用向量的平移、伸缩、合成、分解等变换,正确地进行向量的各种运算,进一步加深对“向量”这一二维性的量的本质的认识,并体会用向量处理问题的优越性。二是向量的坐标运算体现了数与形互相转化和密切结合的思想,所以要通过向量法和坐标法的运用,进一步体会数形结合思想在解决数学问题上的作用。
在解决解斜三角形问题时,一方面要体会向量方法在解三角形方面的应用,另一方面要体会解斜三角形是重要的测量手段,通过学习提高解决实际问题的能力。
五、典型例题
平面向量
【例1】 在下列各命题中为真命题的是( )
①若![]() =(x1,y1)、
=(x1,y1)、![]() =(x2,y2),则
=(x2,y2),则![]() ·
·![]() =x1y1+x2y2
=x1y1+x2y2
②若A(x1,y1)、B(x2,y2),则|![]() |=
|=![]()
③若![]() =(x1,y1)、
=(x1,y1)、![]() =(x2,y2),则
=(x2,y2),则![]() ·
·![]() =0
=0![]() x1x2+y1y2=0
x1x2+y1y2=0
④若![]() =(x1,y1)、
=(x1,y1)、![]() =(x2,y2),则
=(x2,y2),则![]() ⊥
⊥![]()
![]() x1x2+y1y2=0
x1x2+y1y2=0
A、①② B、②③ C、③④ D、①④
解:根据向量数量积的坐标表示;若![]() =(x1,y1),
=(x1,y1), ![]() =(x2,y2),则
=(x2,y2),则![]() ·
·![]() =x1x2+y1y2,对照命题(1)的结论可知,它是一个假命题、
=x1x2+y1y2,对照命题(1)的结论可知,它是一个假命题、
于是对照选择支的结论、可以排除(A)与(D),而在(B)与(C)中均含有(3)、故不必对(3)进行判定,它一定是正确的、对命题(2)而言,它就是两点间距离公式,故它是真命题,这样就以排除了(C),应选择(B)、
说明:对于命题(3)而言,由于![]() ·
·![]() =0
=0![]()
![]() =
=![]() 或
或![]() =
=![]() 或
或![]() ⊥
⊥![]()
![]() x1x2+y1y2=0,故它是一个真命题、
x1x2+y1y2=0,故它是一个真命题、
而对于命题(4)来讲,![]() ⊥
⊥![]()
![]() x1x2+y1y2=0、但反过来,当x1x2+y1y2=0时,可以是x1=y1=0,即
x1x2+y1y2=0、但反过来,当x1x2+y1y2=0时,可以是x1=y1=0,即![]() =
=![]() ,而我们的教科书并没有对零向量是否与其它向量垂直作出规定,因此x1x2+y1y2=0
,而我们的教科书并没有对零向量是否与其它向量垂直作出规定,因此x1x2+y1y2=0![]()
![]() ⊥
⊥![]() ),所以命题(4)是个假命题、
),所以命题(4)是个假命题、
【例2】
已知![]() =(-
=(-![]() ,-1),
,-1), ![]() =(1,
=(1, ![]() ),那么
),那么![]() ,
,![]() 的夹角θ=( )
的夹角θ=( )
A、30° B、60° C、120° D、150°
解:![]() ·
·![]() =(-
=(-![]() ,-1)·(1,
,-1)·(1,![]() )=-2
)=-2![]()
|![]() |=
|=![]() =2
=2
|![]() |=
|=![]() =2
=2
∴cosθ=![]() =
=![]() =
=![]()
【例3】
已知![]() =(2,1),
=(2,1), ![]() =(-1,3),若存在向量
=(-1,3),若存在向量![]() 使得:
使得:![]() ·
·![]() =4,
=4, ![]() ·
·![]() =-9,试求向量
=-9,试求向量![]() 的坐标、
的坐标、
解:设![]() =(x,y),则由
=(x,y),则由![]() ·
·![]() =4可得:
=4可得:
2x+y=4;又由![]() ·
·![]() =-9可得:-x+3y=-9
=-9可得:-x+3y=-9
于是有:![]()
![]()
由(1)+2(2)得7y=-14,∴y=-2,将它代入(1)可得:x=3
∴![]() =(3,-2)、
=(3,-2)、
说明:已知两向量![]() ,
,![]() 可以求出它们的数量积
可以求出它们的数量积![]() ·
·![]() ,但是反过来,若已知向量
,但是反过来,若已知向量![]() 及数量积
及数量积![]() ·
·![]() ,却不能确定
,却不能确定![]() 、
、
【例4】
求向量![]() =(1,2)在向量
=(1,2)在向量![]() =(2,-2)方向上的投影、
=(2,-2)方向上的投影、
解:设向量![]() 与
与![]() 的夹角θ、
的夹角θ、
有cosθ=![]() =
=![]() =-
=-![]()
∴![]() 在
在![]() 方向上的投影=|
方向上的投影=|![]() |cosθ=
|cosθ=![]() ×(-
×(-![]() )=-
)=-![]()
【例5】
已知△ABC的顶点分别为A(2,1),B(3,2),C(-3,-1),BC边上的高AD,求![]() 及点D的坐标、
及点D的坐标、
解:设点D的坐标为(x,y)
∵AD是边BC上的高,
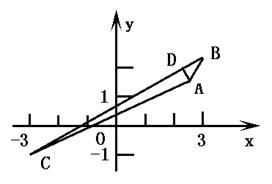 ∴AD⊥BC,∴
∴AD⊥BC,∴![]() ⊥
⊥![]()
又∵C、B、D三点共线,
∴![]() ∥
∥![]()
又![]() =(x-2,y-1),
=(x-2,y-1),
![]() =(-6,-3)
=(-6,-3)
![]() =(x-3,y-2)
=(x-3,y-2)
∴![]()
解方程组,得x=![]() ,y=
,y=![]()
∴点D的坐标为(![]() ,
,![]() ),
),![]() 的坐标为(-
的坐标为(-![]() ,
,![]() )
)
【例6】
设向量![]() 、
、![]() 满足:|
满足:|![]() |=|
|=|![]() |=1,且
|=1,且![]() +
+![]() =(1,0),求
=(1,0),求![]() ,
,![]() 、
、
解:∵|![]() |=|
|=|![]() |=1,
|=1,
∴可设![]() =(cosα,sinα),
=(cosα,sinα),
![]() =(cosβ,sinβ)、
=(cosβ,sinβ)、
∵![]() +
+![]() =(cosα+cosβ,sinα+sinβ)=(1,0),
=(cosα+cosβ,sinα+sinβ)=(1,0),
![]()
由(1)得:cosα=1-cosβ……(3)
由(2)得:sinα=-sinβ……(4)
∴cosα=1-cosβ=![]()
∴sinα=±![]() ,sinβ=
,sinβ=![]()
![]()
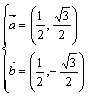 或
或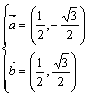
【例7】
对于向量的集合A={![]() =(x,y)|x2+y2≤1}中的任意两个向量
=(x,y)|x2+y2≤1}中的任意两个向量![]() 、
、![]() 与两个非负实数α、β;求证:向量α
与两个非负实数α、β;求证:向量α![]() +β
+β![]() 的大小不超过α+β、
的大小不超过α+β、
证明:设![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2)
=(x2,y2)
根据已知条件有:x21+y21≤1,x22+y22≤1
又因为|α![]() +β
+β![]() |=
|=![]()
=![]()
其中x1x2+y1y2≤![]()
![]() ≤1
≤1
所以|α![]() +β
+β![]() |≤
|≤![]() =|α+β|=α+β
=|α+β|=α+β
【例8】
已知梯形ABCD中,AB∥CD,∠CDA=∠DAB=90°,CD=DA=![]() AB、
AB、
求证:AC⊥BC
证明:以A为原点,AB所在直线为x轴,建立直角坐标系、如图,设AD=1
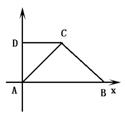 则A(0,0)、B(2,0)、C(1,1)、D(0,1)
则A(0,0)、B(2,0)、C(1,1)、D(0,1)
∴![]() =(-1,1),
=(-1,1), ![]() =(1,1)
=(1,1)
![]() ·
·![]() =-1×1+1×1=0
=-1×1+1×1=0
∴BC⊥AC、
【例9】 已知A(0,a),B(0,b),(0<a<b),在x轴的正半轴上求点C,使∠ACB最大,并求出最大值、
解,设C(x,0)(x>0)
则![]() =(-x,a),
=(-x,a), ![]() =(-x,b)
=(-x,b)
则![]() ·
·![]() =x2+ab、
=x2+ab、
cos∠ACB=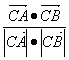 =
=![]()
令t=x2+ab
故cos∠ACB=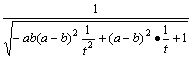
当![]() =
=![]() 即t=2ab时,cos∠ACB最大值为
即t=2ab时,cos∠ACB最大值为![]() 、
、
当C的坐标为(![]() ,0)时,∠ACB最大值为arccos
,0)时,∠ACB最大值为arccos![]() 、
、
【例10】
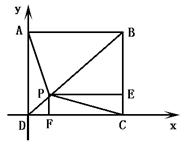 如图,四边形ABCD是正方形,P是对角线BD上的一点,PECF是矩形,用向量法证明
如图,四边形ABCD是正方形,P是对角线BD上的一点,PECF是矩形,用向量法证明
(1)PA=EF (2)PA⊥EF
证明:建立如图所示坐标系,设正方形边长为1,
|![]() |=λ,则A(0,1),P(
|=λ,则A(0,1),P(![]() λ,
λ,![]() λ),E(1,
λ),E(1,![]() λ),F(
λ),F(![]() λ,0)
λ,0)
∴![]() =(-
=(-![]() λ,1-
λ,1-![]() λ),
λ), ![]() =(
=(![]() λ-1,-
λ-1,- ![]() λ)
λ)
(1)|![]() |2=(-
|2=(-![]() λ)2+(1-
λ)2+(1-![]() λ)2=λ2-
λ)2=λ2-![]() λ+1
λ+1
|![]() |2=(
|2=(![]() λ-1)2+(-
λ-1)2+(-![]() λ)2=λ2-
λ)2=λ2-![]() λ+1
λ+1
∴|![]() |2=|
|2=|![]() |2,故PA=EF
|2,故PA=EF
(2) ![]() ·
·![]() =(-
=(-![]() λ)(
λ)(![]() λ-1)+(1-
λ-1)+(1-![]() λ)(-
λ)(-![]() λ)=0
λ)=0
∴![]() ⊥
⊥![]() ∴PA⊥EF、
∴PA⊥EF、
【例11】
已知![]()
① 求![]() ;
;
②当k为何实数时,k![]()
![]() 与
与![]() 平行, 平行时它们是同向还是反向?
平行, 平行时它们是同向还是反向?
解:①![]() = (1,0) + 3(2,1) = ( 7,3) , ∴
= (1,0) + 3(2,1) = ( 7,3) , ∴![]() =
= ![]() =
=![]() .
.
②k![]()
![]() = k(1,0)-(2,1)=(k-2,-1).
= k(1,0)-(2,1)=(k-2,-1).
设k![]()
![]() =λ(
=λ(![]() ),即(k-2,-1)=
λ(7,3),
),即(k-2,-1)=
λ(7,3),
∴![]()
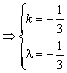 .
.
故k= ![]() 时, 它们反向平行.
时, 它们反向平行.
【例12】
已知![]()
![]() 与
与![]() 的夹角为
的夹角为![]() ,若向量
,若向量![]() 与
与![]() 垂直, 求k.
垂直, 求k.
解:![]() =2×1×
=2×1×![]() =1.
=1.
∵![]() 与
与![]() 垂直,
垂直,
∴(![]() )
)![]() =
= ![]() ,
,
∴2![]()
![]() k = - 5.
k = - 5.
【例13】 如果△ABC的三边a、b、c满足b2 + c 2 = 5a2,BE、CF分别为AC边与AB上的中线, 求证:BE⊥CF.
解:
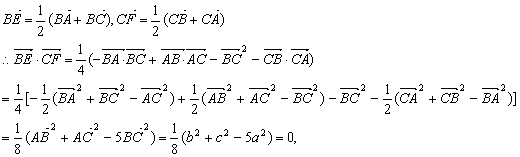
∴![]() ⊥
⊥![]() , 即 BE⊥CF .
, 即 BE⊥CF .
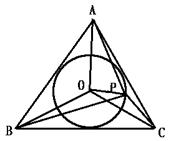
【例14】 是否存在4个平面向量,两两不共线,其中任何两个向量之和均与其余两个向量之和垂直?
解:如图所示,在正△ABC中,O为其内心,P为圆周上一点,
满足![]() ,
,![]() ,
,![]() ,
,![]() 两两不共线,有
两两不共线,有
(![]() +
+![]() )·(
)·(![]() +
+![]() )
)
=(![]() +
+![]() +
+![]() +
+![]() )·(
)·(![]() +
+![]() +
+![]() )
)
 =(2
=(2![]() +
+![]() +
+![]() )·(2
)·(2![]() +
+![]() )
)
=(2![]() -
-![]() )·(2
)·(2![]() +
+![]() )
)
=4![]() 2-
2-![]() 2
2
=4![]() 2-
2-![]() 2=0
2=0
有(![]() +
+![]() )与(
)与(![]() +
+![]() )垂直、
)垂直、
同理证其他情况、从而![]() ,
,![]() ,
,![]() ,
,![]() 满足题意、故存在这样4个平面向量、
满足题意、故存在这样4个平面向量、
平面向量的综合应用
1.利用向量的坐标运算,解决两直线的夹角,判定两直线平行、垂直问题
【例1】
已知向量![]() 满足条件
满足条件![]() ,
,![]() ,求证:
,求证:![]() 是正三角形
是正三角形
解:令O为坐标原点,可设![]()
由![]() ,即
,即![]()
|
|
两式平方和为![]() ,
,![]() ,
,
由此可知![]() 的最小正角为
的最小正角为![]() ,即
,即![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
同理可得![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
这说明![]() 三点均匀分部在一个单位圆上,
三点均匀分部在一个单位圆上,
所以![]() 为等腰三角形.
为等腰三角形.
【例2】 求等腰直角三角形中两直角边上的中线所成的钝角的度数
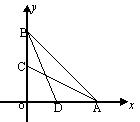 解:如图,分别以等腰直角三角形的两直角边为
解:如图,分别以等腰直角三角形的两直角边为![]() 轴、
轴、![]()
轴建立直角坐标系,设![]() ,则
,则![]() ,
,
从而可求:![]() ,
,
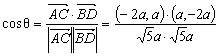 =
=![]() .
.
![]() .
.
2.利用向量的坐标运算,解决有关线段的长度问题
【例3】
已知![]() ,AD为中线,求证
,AD为中线,求证![]()
证明:以B为坐标原点,以BC所在的直线为![]() 轴建立如图2直角坐标系,
轴建立如图2直角坐标系,
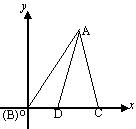 设
设![]() ,
,![]() ,
,
则![]() ,
,
 .
.
=![]() ,
,
从而![]()
 ,
,
![]() .
.
3.利用向量的坐标运算,用已知向量表示未知向量
【例4】
已知点![]() 是
是![]()
![]() 且
且![]() 试用
试用![]()
解:以O为原点,OC,OB所在的直线为![]() 轴和
轴和![]() 轴建立如图3所示的坐标系.
轴建立如图3所示的坐标系.
由OA=2,![]() ,所以
,所以![]() ,
,
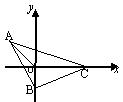 易求
易求![]() ,设
,设
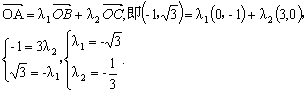
![]() .
.
【例5】 如图,
![]()
用![]() 表示
表示![]()
解:以O为坐标原点,以OA所在的直线为![]() 轴,建立如图所示的直角坐标系,则
轴,建立如图所示的直角坐标系,则![]() ,
,![]()
![]()
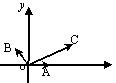
![]()
![]()
![]() .
.
4.利用向量的数量积解决两直线垂直问题
【例6】
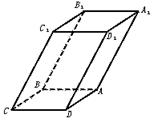 如图,已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
如图,已知平行六面体ABCD—A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD.
(1)求证:C1C⊥BD.
(2)当![]() 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
(1)证明:设![]() =a,
=a, ![]() =b,
=b,![]() =c,依题意,a=b,
=c,依题意,a=b,![]() 、
、![]() 、
、![]() 中两两所成夹角为θ,于是
中两两所成夹角为θ,于是![]() =a-b,
=a-b,![]() =c(a-b)=c·a-c·b=c·acosθ-c·bcosθ=0,∴C1C⊥BD.
=c(a-b)=c·a-c·b=c·acosθ-c·bcosθ=0,∴C1C⊥BD.
(2)解:若使A1C⊥平面C1BD,只须证A1C⊥BD,A1C⊥DC1,
由![]()
=(a+b+c)·(a-c)=a2+a·b-b·c-c2=a2-c2+b·acosθ-b·c·cosθ=0,得
当a=c时,A1C⊥DC1,同理可证当a=c时,A1C⊥BD,
∴![]() =1时,A1C⊥平面C1BD.
=1时,A1C⊥平面C1BD.
【例7】
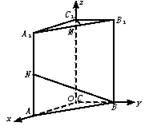 如图,直三棱柱ABC—A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABC—A1B1C1,底面△ABC中,CA=CB=1,∠BCA=90°,AA1=2,M、N分别是A1B1、A1A的中点.
(1)求![]() 的长;
的长;
(2)求cos<![]() >的值;
>的值;
(3)求证:A1B⊥C1M.
解:(1)如图,以C为原点建立空间直角坐标系O-xyz.
依题意得:B(0,1,0),N(1,0,1)
∴![]() =
=![]() .
.
(2)解:依题意得:A1(1,0,2),C(0,0,0),B1(0,1,2).
∴![]() =
=![]() =(0,1,2)
=(0,1,2)
![]() =1×0+(-1)×1+2×2=3
=1×0+(-1)×1+2×2=3
![]() =
=![]()
![]()
![]()
(3)证明:依题意得:C1(0,0,2),M(![]() )
)
![]()
∴![]()
∴A1B⊥C1M.
5.利用向量的数量积解决有关距离的问题,距离问题包括点到点的距离,点的线的距离,点到面的距离,线到线的距离,线到面的距离,面到面的距离.
【例8】
求平面内两点![]() 间的距离公式
间的距离公式
解:设点![]() ,
,![]()
![]() ,而
,而![]()
![]() 点
点![]() 与点
与点![]() 之间的距离为:
之间的距离为:![]()
6.利用向量的数量积解决线与线的夹角及面与面的夹角问题.
【例9】
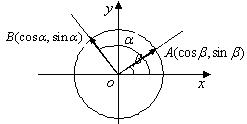 证明:
证明:
![]()
证明:在单位圆![]() 上任取两点
上任取两点![]() ,以
,以![]() 为始边,以
为始边,以![]() 为终边的角分别为
为终边的角分别为![]() ,则
,则![]() 点坐标为
点坐标为![]()
![]() 点坐标为
点坐标为![]() ;
;
则向量![]()
![]()
![]()
![]() ,它们的夹角为
,它们的夹角为![]() ,
,
![]()
![]() ,由向量夹角公式得:
,由向量夹角公式得:
![]()
![]() ,从而得证.
,从而得证.
注:用同样的方法可证明![]()
![]()
7.利用向量的数量积解决有关不等式、最值问题.
【例10】
证明柯西不等式![]()
证明:令![]()
(1)
当![]() 或
或![]() 时,
时,![]() ,结论显然成立;
,结论显然成立;
(2)
当![]() 且
且![]() 时,令
时,令![]() 为
为![]() 的夹角,则
的夹角,则![]()
![]()
![]() . 又
. 又![]()
![]()
![]() (当且仅当
(当且仅当![]() 时等号成立)
时等号成立)
![]()
![]()
![]() .(当且仅当
.(当且仅当![]() 时等号成立)
时等号成立)
【例11】
求![]() 的最值
的最值
解:原函数可变为![]() ,
,
所以只须求![]() 的最值即可,
的最值即可,
构造![]() ,
,
那么![]() .
.
故![]() .
.
【例12】 三角形ABC中,A(5,-1)、B(-1,7)、C(1,2),求:(1)BC边上的中线
AM的长;(2)∠CAB的平分线AD的长;(3)cosABC的值.
解:(1)点M的坐标为xM=![]()
![]()
![]()
D点分![]() 的比为2.
的比为2.
∴xD=![]()
![]()
(3)∠ABC是![]() 与
与![]() 的夹角,而
的夹角,而![]() =(6,8),
=(6,8),![]() =(2,-5).
=(2,-5).
解斜三角形
【例1】
已知△ABC的三个内角A、B、C满足A+C=2B.![]() ,求cos
,求cos![]() 的值.
的值.
解法一:由题设条件知B=60°,A+C=120°.
设α=![]() ,则A-C=2α,可得A=60°+α,C=60°-α,
,则A-C=2α,可得A=60°+α,C=60°-α,
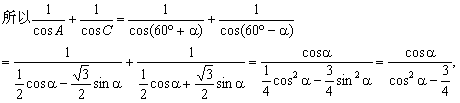
依题设条件有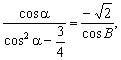
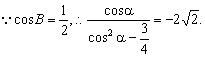
整理得4![]() cos2α+2cosα-3
cos2α+2cosα-3![]() =0(M)
=0(M)
(2cosα-![]() )(2
)(2![]() cosα+3)=0,∵2
cosα+3)=0,∵2![]() cosα+3≠0,
cosα+3≠0,
∴2cosα-![]() =0.从而得cos
=0.从而得cos![]() .
.
解法二:由题设条件知B=60°,A+C=120°
![]() ①,把①式化为cosA+cosC=-2
①,把①式化为cosA+cosC=-2![]() cosAcosC ②,
cosAcosC ②,
利用和差化积及积化和差公式,②式可化为
![]() ③,
③,
将cos![]() =cos60°=
=cos60°=![]() ,cos(A+C)=-
,cos(A+C)=-![]() 代入③式得:
代入③式得:
![]() ④
④
将cos(A-C)=2cos2(![]() )-1代入
④:4
)-1代入
④:4![]() cos2(
cos2(![]() )+2cos
)+2cos![]() -3
-3![]() =0,(*),
=0,(*),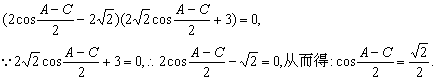
【例2】
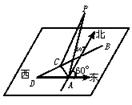 在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北30°东,俯角为60°的B处,到11时10分又测得该船在岛北60°西、俯角为30°的C处。
在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北30°东,俯角为60°的B处,到11时10分又测得该船在岛北60°西、俯角为30°的C处。
(1)求船的航行速度是每小时多少千米;
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?
解:(1)在Rt△PAB中,∠APB=60° PA=1,∴AB=![]() (千米)
(千米)
在Rt△PAC中,∠APC=30°,∴AC=![]() (千米)
(千米)
在△ACB中,∠CAB=30°+60°=90°
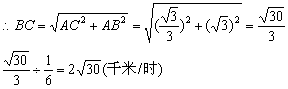
(2)∠DAC=90°-60°=30°
sinDCA=sin(180°-∠ACB)=sinACB=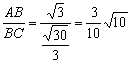
sinCDA=sin(∠ACB-30°)=sinACB·cos30°-cosACB·sin30°![]() .
.
![]()
在△ACD中,据正弦定理得![]() ,
,
∴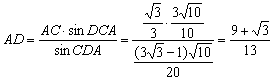
答:此时船距岛A为![]() 千米.
千米.
【例3】
已知△ABC的三内角A、B、C满足A+C=2B,设x=cos![]() ,f(x)=cosB(
,f(x)=cosB(![]() ).
).
(1)试求函数f(x)的解析式及其定义域;
(2)判断其单调性,并加以证明;
(3)求这个函数的值域.
解:(1)∵A+C=2B,∴B=60°,A+C=120°
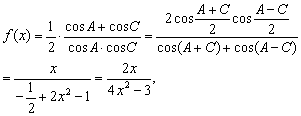
∵0°≤![]() <60°,∴x=cos
<60°,∴x=cos![]() ∈(
∈(![]() ,1
,1![]()
又4x2-3≠0,∴x≠![]() ,∴定义域为(
,∴定义域为(![]() ,
,![]() )∪(
)∪(![]() ,1].
,1].
(2)设x1<x2,∴f(x2)-f(x1)=![]()
=![]() ,若x1,x2∈(
,若x1,x2∈(![]() ),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0
),则4x12-3<0,4x22-3<0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0
即f(x2)<f(x1),若x1,x2∈(![]() ,1],则4x12-3>0.
,1],则4x12-3>0.
4x22-3>0,4x1x2+3>0,x1-x2<0,∴f(x2)-f(x1)<0.
即f(x2)<f(x1),∴f(x)在(![]() ,
,![]() )和(
)和(![]() ,1
,1![]() 上都是减函数.
上都是减函数.
(3)由(2)知,f(x)<f(![]() )=-
)=-![]() 或f(x)≥f(1)=2.
或f(x)≥f(1)=2.
故f(x)的值域为(-∞,-![]() )∪[2,+∞
)∪[2,+∞![]() .
.
【例4】
在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() .若
.若![]() ,求角
,求角![]() .
.
解:由正弦定理,将已知等式中的边转化为角.可得
![]() .
.
因为![]() ,故有
,故有![]() ,
,
∴
![]() .
.
又∵ ![]() ,
,
∴ ![]() ,
,
即![]() ,
,
由![]() ,可解得
,可解得![]() .
.
【例5】
在△ABC中,已知![]() .
.
(1)若任意交换![]() 的位置,
的位置,![]() 的值是否会发生变化?试证明你的结论;
的值是否会发生变化?试证明你的结论;
(2)求![]() 的最大值.
的最大值.
解:(1)∵
![]()
![]()
![]()
![]()
![]()
![]() ,
,
∴ 任意交换![]() 的位置,
的位置,![]() 的值不会发生变化.
的值不会发生变化.
(2)
解法1:将![]() 看作是关于
看作是关于![]() 的二次函数.
的二次函数.
![]()
![]() .
.
所以,当![]() ,且
,且![]() 取到最大值1时,也即
取到最大值1时,也即![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
解法2:用调整的方法, 也即对于每个固定的![]() 的值,去调整
的值,去调整![]() ,求出
,求出![]() 取得最大值时
取得最大值时![]() 所满足的条件.
所满足的条件.
对于![]() ,如果固定
,如果固定![]() ,则可将
,则可将![]() 看作是关于
看作是关于![]() 的一次或常数函数.为了讨论其最大值,显然应该考虑
的一次或常数函数.为了讨论其最大值,显然应该考虑![]() 的符号,并由此展开讨论.
的符号,并由此展开讨论.
若![]() ,则
,则![]() ,所以,
,所以,![]() ,所以,
,所以,
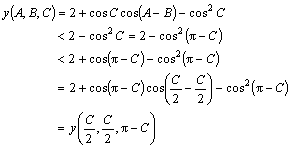
所以,只需考虑![]() 的情形.此时
的情形.此时![]() 是关于
是关于![]() 的常数函数或单调递增的一次函数,因此,最大值必可在
的常数函数或单调递增的一次函数,因此,最大值必可在![]() (即
(即![]() )时取得.所以,
)时取得.所以,
![]()
![]() ,
,
等号当且仅当![]() 时取得.
时取得.
六、专题练习
【平面向量练习】
一、选择题:
1、下列各式中正确的是( C )
(1)(λ·a) ·b=λ·(a b)=a· (λb), (2)a·b=a·b,
(3)(a ·b)· c=a · (b ·c), (4)(a+b) · c= a·c+b·c
A.(1)(3) B.(2)(4) C.(1)(4) D.以上都不对.
2、在ΔABC中,若(![]() +
+![]() )·(
)·(![]() -
-![]() )=0,则ΔABC为( C
)
)=0,则ΔABC为( C
)
A.正三角形 B.直角三角形 C.等腰三角形 D.无法确定
3、若a=b=a-b,则b与a+b的夹角为( A )
A.30° B.60° C.150° D.120°
4、已知a=1,b=![]() ,且(a-b)和a垂直,则a与b的夹角为( D
)
,且(a-b)和a垂直,则a与b的夹角为( D
)
A.60° B.30° C.135° D.45°
5、若![]() ·
·![]() +
+ ![]() = 0,则ΔABC为( A )
= 0,则ΔABC为( A )
A.直角三角形 B.钝角三角形 C.锐角三角形 D.等腰直角三角形
6、设a= 4,b= 3, 夹角为60°, 则a+b等于( C )
A.37
B.13 C.![]() D.
D.![]()
7、己知a=1,b=2, a与b的夹角为600,c =3a+b, d =λa-b ,若c⊥d,则实数λ的值为( C )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、设 a,b,c是平面内任意的非零向量且相互不共线,则( D )
①(ab)c-(ca)b=0 ②a -b< a-b
③(bc)a-(ca)b不与c垂直 ④(3a+2b)(3a-2b)= 9a2-4b2
其中真命题是 ( )
A.①② B.②③ C.③④ D.②④
二、填空题:
9、已知e是单位向量,求满足a∥e且a·e=-18的向量a=__________.-18e
10、设a=(m+1)i-3j, b=i+(m-1)j, (a+b) ⊥(a-b), 则m=________.-2
11、a=5, b=3,a-b=7,则a、b的夹角为__________. 120°
12、 a与d=b-![]() 关系为________. a⊥b
关系为________. a⊥b
三、解答题:
13、已知 a=4,b=5,a+b=![]() ,求:① a·b ;②(2a-b) ·(a+3b)
,求:① a·b ;②(2a-b) ·(a+3b)
解:①a+b2=(a+b)2=a2+2ab+b2=a2+2a·b+b2,
![]() =
=![]() .
.
②(2a-b)·(a+3b)=2a2+5a·b-3b2=2a2+5a·b-3b2
=2×42+5×(-10)-3×52=-93.
14、四边形ABCD中,![]() = a,
= a, ![]() = b,
= b,![]() = c,
= c,
![]() = d,且a·b=b·c=c·d=d
·a,判断四边形ABCD是什么图形?
= d,且a·b=b·c=c·d=d
·a,判断四边形ABCD是什么图形?
分析:在四边形ABCD中,a+b+c+d=0,这是一个隐含条件,
对a+b=-(c+d),两边平方后,用a·b=b·c=d·c代入,
从四边形的边长与内角的情况来确定四边形的形状.
解:∵a+b+c+d=0,∴a+b=-(c+d),
∴(a+b)2=(c+d)2,即a2+2a·b+b2=c2+2c·d+d2,
∵a·b=c·d,∴a2+b2=c2+d2……①
同理:a2+d2=b2+c2……②
①,②两式相减得:b2=d2,a2=c2,即b=d,a=c.
∴ABCD为平行四边形.
又∵a·b=b·c,即b·(a-c)=0,而a=-c,
∵b·(2a)=0
∴a⊥b,
∴四边形ABCD为矩形.
15、已知:a=5,b=4,且a与b的夹角为60°,问当且仅当k为何值时,向量ka-b与 a+2b
垂直?
解:![]()
![]()
![]() .
.
【平面向量的综合应用练习】
一、选择题
1.设A、B、C、D四点坐标依次是(-1,0),(0,2),(4,3),(3,1),则四边形ABCD为( )
A.正方形 B.矩形
C.菱形 D.平行四边形
2.已知△ABC中,![]() =a,
=a,![]() =b,a·b<0,S△ABC=
=b,a·b<0,S△ABC=![]() ,a=3,b=5,则a与b的夹角是( )
,a=3,b=5,则a与b的夹角是( )
A.30° B.-150° C.150° D.30°或150°
二、填空题
3.将二次函数y=x2的图象按向量a平移后得到的图象与一次函数y=2x-5的图象只有一个公共点(3,1),则向量a=_________.
4.等腰△ABC和等腰Rt△ABD有公共的底边AB,它们所在的平面成60°角,若AB=16 cm,AC=17 cm,则CD=_________.
 三、解答题
三、解答题
5.如图,在△ABC中,设![]() =a,
=a,![]() =b,
=b,![]() =c,
=c, ![]() =λa,(0<λ<1),
=λa,(0<λ<1),![]() =μb(0<μ<1),试用向量a,b表示c.
=μb(0<μ<1),试用向量a,b表示c.
6.正三棱柱ABC—A1B1C1的底面边长为a,侧棱长为![]() a.
a.
(1)建立适当的坐标系,并写出A、B、A1、C1的坐标;
(2)求AC1与侧面ABB1A1所成的角.
7.已知两点M(-1,0),N(1,0),且点P使![]() 成公差小于零的等差数列.
成公差小于零的等差数列.
(1)点P的轨迹是什么曲线?
(2)若点P坐标为(x0,y0),Q为![]() 与
与![]() 的夹角,求tanθ.
的夹角,求tanθ.
8.已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明:BD∥平面EFGH;
(3)设M是EG和FH的交点,求证:对空间任一点O,有![]() .参考答案
.参考答案
一、1.解析:![]() =(1,2),
=(1,2),![]() =(1,2),∴
=(1,2),∴![]() =
=![]() ,∴
,∴![]() ∥
∥![]() ,又线段AB与线段DC无公共点,∴AB∥DC且AB=DC,∴ABCD是平行四边形,又
,又线段AB与线段DC无公共点,∴AB∥DC且AB=DC,∴ABCD是平行四边形,又![]() =
=![]() ,
,![]() =(5,3),
=(5,3),![]() =
=![]() ,∴
,∴![]() ≠
≠![]() },∴ABCD不是菱形,更不是正方形;又
},∴ABCD不是菱形,更不是正方形;又![]() =(4,1),
=(4,1),
∴1·4+2·1=6≠0,∴![]() 不垂直于
不垂直于![]() ,∴ABCD也不是矩形,故选D.
,∴ABCD也不是矩形,故选D.
答案:D
2.解析:∵![]() ·3·5sinα得sinα=
·3·5sinα得sinα=![]() ,则α=30°或α=150°.
,则α=30°或α=150°.
又∵a·b<0,∴α=150°.
答案:C
二、3.(2,0) 4.13 cm
三、5.解:∵![]() 与
与![]() 共线,∴
共线,∴![]() =m
=m![]() =m(
=m(![]() -
-![]() )=m(μb-a),
)=m(μb-a),
∴![]() =
=![]() +
+![]() =a+m(μb-a)=(1-m)a+mμb ①
=a+m(μb-a)=(1-m)a+mμb ①
又![]() 与
与![]() 共线,∴
共线,∴![]() =n
=n![]() =n(
=n(![]() -
-![]() )=n(λa-b),
)=n(λa-b),
∴![]() =
=![]() +
+![]() =b+n(λa-b)=nλa+(1-n)b ②
=b+n(λa-b)=nλa+(1-n)b ②
由①②,得(1-m)a+μmb=λna+(1-n)b.
∵a与b不共线,∴![]() ③
③
解方程组③得:m=![]() 代入①式得c=(1-m)a+mμb=
代入①式得c=(1-m)a+mμb=![]() [λ(1-μ)a+μ(1-λ)b].
[λ(1-μ)a+μ(1-λ)b].
6.解:(1)以点A为坐标原点O,以AB所在直线为Oy轴,以AA1所在直线为Oz轴,以经过原点且与平面ABB1A1垂直的直线为Ox轴,建立空间直角坐标系.
由已知,得A(0,0,0),B(0,a,0),A1(0,0,![]() a),C1(-
a),C1(-![]()
![]() a).
a).
(2)取A1B1的中点M,于是有M(0,![]() a),连AM,MC1,有
a),连AM,MC1,有![]() =(-
=(-![]() a,0,0),
a,0,0),
且![]() =(0,a,0),
=(0,a,0),![]() =(0,0
=(0,0![]() a)
a)
由于![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,所以MC1⊥面ABB1A1,∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角.
=0,所以MC1⊥面ABB1A1,∴AC1与AM所成的角就是AC1与侧面ABB1A1所成的角.
∵![]() =
=![]()
![]()
![]()
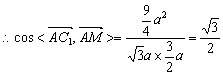
所以![]() 所成的角,即AC1与侧面ABB1A1所成的角为30°.
所成的角,即AC1与侧面ABB1A1所成的角为30°.
7.解:(1)设P(x,y),由M(-1,0),N(1,0)得,![]() =-
=-![]() =(-1-x,-y),
=(-1-x,-y),![]() =(1-x,-y),
=(1-x,-y),![]() =-
=-![]() =(2,0),∴
=(2,0),∴![]() ·
·![]() =2(1+x),
=2(1+x), ![]() ·
·![]() =x2+y2-1,
=x2+y2-1,![]() =2(1-x).于是,
=2(1-x).于是,![]() 是公差小于零的等差数列,等价于
是公差小于零的等差数列,等价于
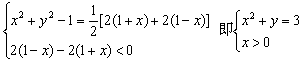
所以,点P的轨迹是以原点为圆心,![]() 为半径的右半圆.
为半径的右半圆.
(2)点P的坐标为(x0,y0)
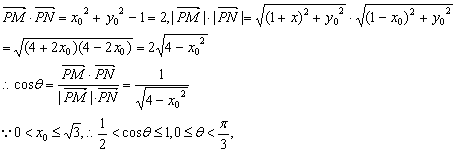
![]()
8.证明:(1)连结BG,则![]()
由共面向量定理的推论知:E、F、G、H四点共面,(其中![]()
![]() =
=![]() )
)
(2)因为![]() .
.
所以EH∥BD,又EH![]() 面EFGH,BD
面EFGH,BD![]() 面EFGH
面EFGH
所以BD∥平面EFGH.
(3)连OM,OA,OB,OC,OD,OE,OG
由(2)知![]() ,同理
,同理![]() ,所以
,所以![]() ,EH
,EH![]() FG,所以EG、FH交于一点M且被M平分,所以
FG,所以EG、FH交于一点M且被M平分,所以
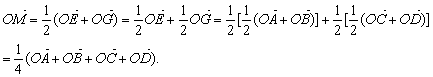 .
.
【解斜三角形练习】
一、选择题
1.给出四个命题:(1)若sin2A=sin2B,则△ABC为等腰三角形;(2)若sinA=cosB,则△ABC为直角三角形;(3)若sin2A+sin2B+sin2C<2,则△ABC为钝角三角形;(4)若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC为正三角形.以上正确命题的个数是( )
A.1 B.2 C.3 D.4
二、填空题
2.在△ABC中,已知A、B、C成等差数列,则![]() 的值为__________.
的值为__________.
3.在△ABC中,A为最小角,C为最大角,已知cos(2A+C)=-![]() ,sinB=
,sinB=![]() ,则cos2(B+C)=__________.
,则cos2(B+C)=__________.
三、解答题
4.已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积.
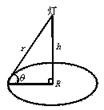 5.如右图,在半径为R的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r的平方成反比,即I=k·
5.如右图,在半径为R的圆桌的正中央上空挂一盏电灯,桌子边缘一点处的照度和灯光射到桌子边缘的光线与桌面的夹角θ的正弦成正比,角和这一点到光源的距离 r的平方成反比,即I=k·![]() ,其中 k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?
,其中 k是一个和灯光强度有关的常数,那么怎样选择电灯悬挂的高度h,才能使桌子边缘处最亮?
6.在△ABC中,a、b、c分别为角A、B、C的对边,![]() .
.
(1)求角A的度数;
(2)若a=![]() ,b+c=3,求b和c的值.
,b+c=3,求b和c的值.
7.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a、b、3c成等比数列,又∠A-∠C=![]() ,试求∠A、∠B、∠C的值.
,试求∠A、∠B、∠C的值.
8.在正三角形ABC的边AB、AC上分别取D、E两点,使沿线段DE折叠三角形时,顶点A正好落在边BC上,在这种情况下,若要使AD最小,求AD∶AB的值.
参考答案
一、1.解析:其中(3)(4)正确.
答案: B
二、2.解析:∵A+B+C=π,A+C=2B,
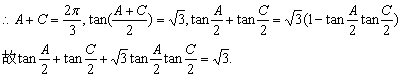
答案:![]()
3.解析:∵A为最小角∴2A+C=A+A+C<A+B+C=180°.
∵cos(2A+C)=-![]() ,∴sin(2A+C)=
,∴sin(2A+C)=![]() .
.
∵C为最大角,∴B为锐角,又sinB=![]() .故cosB=
.故cosB=![]() .
.
即sin(A+C)=![]() ,cos(A+C)=-
,cos(A+C)=-![]() .
.
∵cos(B+C)=-cosA=-cos[(2A+C)-(A+C)]=-![]() ,
,
∴cos2(B+C)=2cos2(B+C)-1=![]() .
.
答案:![]()
三、4.解:如图:连结BD,则有四边形ABCD的面积:
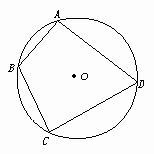
S=S△ABD+S△CDB=![]() ·AB·ADsinA+
·AB·ADsinA+![]() ·BC·CD·sinC
·BC·CD·sinC
∵A+C=180°,∴sinA=sinC
故S=![]() (AB·AD+BC·CD)sinA=
(AB·AD+BC·CD)sinA=![]() (2×4+6×4)sinA=16sinA
(2×4+6×4)sinA=16sinA
由余弦定理,在△ABD中,BD2=AB2+AD2-2AB·AD·cosA=20-16cosA
在△CDB中,BD2=CB2+CD2-2CB·CD·cosC=52-48cosC
∴20-16cosA=52-48cosC,∵cosC=-cosA,
∴64cosA=-32,cosA=-![]() ,又0°<A<180°,∴A=120°故S=16sin120°=8
,又0°<A<180°,∴A=120°故S=16sin120°=8![]() .
.
5.解:R=rcosθ,由此得:![]() ,
,
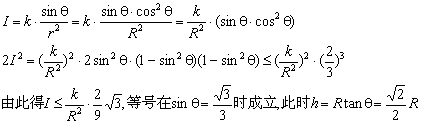
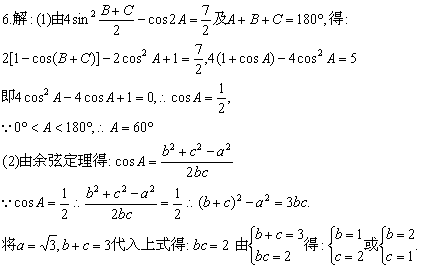
7.解:由a、b、3c成等比数列,得:b2=3ac
∴sin2B=3sinC·sinA=3(-![]() )[cos(A+C)-cos(A-C)]
)[cos(A+C)-cos(A-C)]
∵B=π-(A+C).∴sin2(A+C)=-![]() [cos(A+C)-cos
[cos(A+C)-cos![]() ]
]
即1-cos2(A+C)=-![]() cos(A+C),解得cos(A+C)=-
cos(A+C),解得cos(A+C)=-![]() .
.
∵0<A+C<π,∴A+C=![]() π.又A-C=
π.又A-C=![]() ∴A=
∴A=![]() π,B=
π,B=![]() ,C=
,C=![]() .
.
8.解:按题意,设折叠后A点落在边BC上改称P点,显然A、P两点关于折线DE对称,又设∠BAP=θ,∴∠DPA=θ,∠BDP=2θ,再设AB=a,AD=x,∴DP=x.在△ABC中,
∠APB=180°-∠ABP-∠BAP=120°-θ,
由正弦定理知:![]() .∴BP=
.∴BP=![]()
在△PBD中,![]() ,
,
![]()
∵0°≤θ≤60°,∴60°≤60°+2θ≤180°,∴当60°+2θ=90°,即θ=15°时,
sin(60°+2θ)=1,此时x取得最小值![]() a,即AD最小,
a,即AD最小,
∴AD∶DB=2![]() -3.
-3.