08高考数学填空题专项训练7

填空题专项训练(7)

1．已知集合，，则　　　　　　　　  .

2．函数的图象不经过第二象限，则t的取值范围是　　　　　　　　　　 ．

3．定义一种运算：，例如：12=1，32=2，则函数 的值域为　 　　．

4．圆关于直线对称的圆的方程是 　 ．

5．设为实数，且，则　  　　．

6．已知a=，b=3，a和b的夹角为45°，求当向量λa+ b与a+λb的夹角为锐角时，λ的取值范围是　　 　　　　　．

7．已知数列的前n项和为，则数列的前n项和=　　　　　．

8．设动点坐标满足，则的最小值为　 　　　　．

9．不等式的解集是空集，则实数的取值范围是　　　　　　.

10．给出四个命题：（1）“成等比数列”是“函数f (x)=ax²+bx+c的图像与x轴没有公共点”的充分不必要条件；（2）若{}成等比数列，是前n项和，则成等比数列；（3）中，若三边成等比数列，则公比；（4）若没有实根，则；

（5）若等差数列{}的前n项和为，则三点共线．

其中假命题的序号为　　　　　　　　　　　．

11．设，，是空间的三条直线，下面给出四个命题：

①若，，则；②若、是异面直线，、是异面直线，则、也是异面直线；③若和相交，和相交，则和也相交；④若和共面，和共面，则和也共面．其中真命题的个数是________个

12．在中，若，则的外接圆半径，将此结论拓展到空间，可得出的正确结论是：在四面体中，若两两垂直，，则四面体的外接球半径____________．

13．2002年8月在北京召开了国际数学家大会, 会标如图示, 它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形, 若直角三角形中较小的锐角为θ, 大正方形面积是1, 小正方形面积是, 则的值是_____________________．

14．一水池有两个进水口，一个出水口，每水口的进出水速度如图甲、乙所示．某天0点到6点，该水池的蓄水量如图丙所示．（至少打开一个水口）

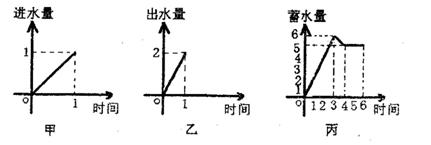
给出以下3个论断：①0点到3点只进水不出水；②3点到4点不进水只出水；③4点到6点不进水不出水，则一定能确定正确的诊断是　　　 ．

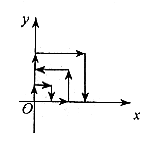
15. 如图，一个粒子在第一象限运动，在第一秒末，它从原点运动到（0，1），接着它按如图所示的x轴、y轴的平行方向来回运动，（即（0，0）→（0，1）→（1，1）→（1，0）→（2，0）→…），且每秒移动一个单位，那么第2008秒末这个粒子所处的位置的坐标为______。