08高考数学复习函数训练题(一)
1![]() 设函数y=f(x)的图象关于直线x=1对称,在x≤1时,f(x)=(x+1)2-1,则x>1时f(x)等于( )
设函数y=f(x)的图象关于直线x=1对称,在x≤1时,f(x)=(x+1)2-1,则x>1时f(x)等于( )
A![]() f(x)=(x+3)2-1
B
f(x)=(x+3)2-1
B![]() f(x)=(x-3)2-1 C
f(x)=(x-3)2-1 C![]() f(x)=(x-3)2+1 D
f(x)=(x-3)2+1 D![]() f(x)=(x-1)2-1
f(x)=(x-1)2-1
2 函数y=x2+![]() (x≤-
(x≤-![]() )的值域是( )
)的值域是( )
A![]() (-∞,-
(-∞,-![]()
![]() B
B![]() [-
[-![]() ,+∞
,+∞![]() C
C![]() [
[![]() ,+∞
,+∞![]() D
D![]() (-∞,-
(-∞,-![]() )
)
3![]() 下列函数中的奇函数是( )
下列函数中的奇函数是( )
A![]() f(x)=(x-1)
f(x)=(x-1)![]() B
B![]() f(x)=
f(x)=![]()
C![]() f(x)=
f(x)=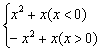 D
D![]() f(x)=
f(x)=![]()
4![]() 函数f(x)=
函数f(x)=![]() 的图象( )
的图象( )
A![]() 关于x轴对称 B
关于x轴对称 B![]() 关于y轴对称
关于y轴对称
C![]() 关于原点对称 D
关于原点对称 D![]() 关于直线x=1对称
关于直线x=1对称
5![]() 设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7
设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x,则f(7![]() 5)等于( )
5)等于( )
A![]() 0
0![]() 5 B
5 B![]() -0
-0![]() 5 C
5 C![]() 1
1![]() 5 D
5 D![]() -1
-1![]() 5
5
6![]() 已知定义域为(-1,1)的奇函数y=f(x)又是减函数,且f(a-3)+f(9-a2)<0, 则a的取值范围是( )
已知定义域为(-1,1)的奇函数y=f(x)又是减函数,且f(a-3)+f(9-a2)<0, 则a的取值范围是( )
A![]() (2
(2![]() ,3) B
,3) B![]() (3,
(3,![]() ) C
) C![]() (2
(2![]() ,4) D
,4) D![]() (-2,3)
(-2,3)
7.(北京卷)已知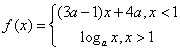 是
是![]() 上的减函数,那么
上的减函数,那么![]() 的取值范围是
的取值范围是
A ![]() B
B ![]() C
C ![]() D
D ![]()
8.(福建卷)已知![]() 是周期为2的奇函数,当
是周期为2的奇函数,当![]() 时,
时,![]() 设
设![]()
![]() 则
则
A ![]() B
B ![]() C
C ![]() D
D ![]()
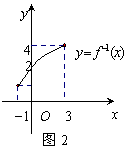 9.(广东卷)函数
9.(广东卷)函数![]() 的反函数
的反函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点
![]() (如图2所示),则方程
(如图2所示),则方程![]() 在
在![]() 上的根是
上的根是![]()
A.4 B.3 C. 2 D.1
10.(江西卷)若不等式x2+ax+1³0对于一切xÎ(0,![]() )成立,则a的最小值是( )
)成立,则a的最小值是( )
A.0 B.
–2
C.-![]() D.-3
D.-3
11.(安徽卷)函数![]() 对于任意实数
对于任意实数![]() 满足条件
满足条件![]() ,若
,若![]() 则
则![]() _______________。
_______________。
12![]() 若f(x)为奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则xf(x)<0的解集为_________
若f(x)为奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则xf(x)<0的解集为_________![]()
13 如果函数f(x)在R上为奇函数,在(-1,0)上是增函数,且f(x+2)=-f(x),试比较f(![]() ),f(
),f(![]() ),f(1)的大小关系_________
),f(1)的大小关系_________![]()
14.我国规定:个人工资、薪金的月总收入不超过800元的免征个人所得税,超过800元部分需征税,全月应纳税的数额(记作![]() )为
)为![]() =全月总收入-800(单位:元)
=全月总收入-800(单位:元)
税率如下表:
|
| 每月应纳税数额 | 税率 |
| |
| 1 |
| 5% | ||
| 2 | 500< | 10% | ||
| 3 | 2000< | 15% | ||
| …… | …… | …… | ||
| 9 | | 45% | ||
某人今年5月份工资、薪金总收入是2645元,则此人5月份应交纳的个人所得税额为_______________________。
15.已知![]()
(1)求![]() 的定义域;
的定义域;
(2)讨论![]() 的增减性;
的增减性;
(3)解方程![]() .
.
16.已知对于x的所有实数值,二次函数f(x)=x2-4ax+2a+12(a∈R)的值都是非负的,求关于x的方程![]() =a-1+2的根的取值范围
=a-1+2的根的取值范围![]()
17.(重庆卷)已知定义域为![]() 的函数
的函数![]() 是奇函数。
是奇函数。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;