08高考数学函数复习训练卷（二）
(1)函数
关于原点对称的曲线为（ ）
（A）
（B）
（C）
（D）
（2）函数f(x)=x
＋b是奇函数的充要条件是（ ）
（A）ab=0 （B）a＋b=0 （C）a=b （D）a2＋b2=0
（3）已知0＜x＜y＜a＜1则有（ ）
（A）loga(xy)＜0 （B）0＜loga(xy)＜1
（C）1＜loga(xy)＜2 （D）loga(xy)＞2
（4）2. 
(
).
(
).2 (
).
(
).4
（5）.若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法计算，参考数据如下表：
| f(1)=-2 | f(1.5)=0.625 |
| f(1.25)=-0.984 | f(1.375)=-0.260 |
| f(1.438)=0.165 | f(1.4065)=-0.052 |
那么方程x3+x2-2x-2=0的一个近似根（精确到0.1）为
(A)1.2 (B)1.3 (C)1.4 (D)1.5
（6）如图所示，fi（x）（i=1，2，3，4）是定义在［0，1］上的四个函数，其中满足性质：“对［0，1］中任意的x1和x2，任意l∈［0，1］，
恒成立”的只有（ ）
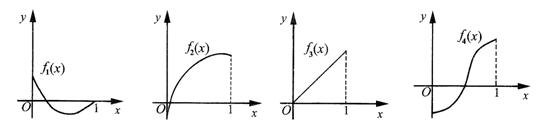
（A）f1（x），f3（x） （B）f2（x）
（C）f2（x），f3（x） （D）f4（x）
(7)若不等式 ax+2 < 6的解集为（－1，2），则实数a等于（ ）
（A）8 （B）2 （C）－4 （D）－8
（8）设函数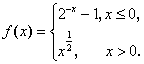
若f(x0)>1，则x0的取值范围是（ ）
（A）（－1，1） （B）（－1，＋∞）
（C）（－∞，－2）∪（0，＋∞） （D）（－∞，－1）∪（1，＋∞）
（9）设
曲线
在点
处切线的倾斜角的取值范围为
，则P到曲线对称轴距离的取值范围为（ ）
（A）[
] （B）
（C）
（D）
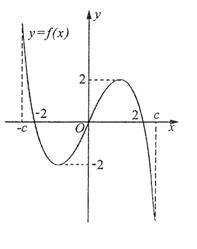
（10）f（x）是定义在区间[－c，c]上的奇函数，其图象如图所示.令g（x）=af（x）+b，则下列关于函数g（x）的叙述正确的是（ ）
（A）若a<0，则函数g（x）的图象关于原点对称.
（B）若a＝1，0<b<2，则方程g（x）=0有大于2的实根.
（C）若a＝－2，b＝0，则函数g（x）的图象关于y轴对称.
（D）若a≠1， b＝2，则方程g（x）=0有三个实根
(11). 函数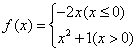
，则
(12).已知函数
的定义域为
，且同时满足下列条件：
（1）
为偶函数
（2）函数没有最小值
（3）函数的图象被
轴截得的线段长为4
请写出符合上述条件的一个函数解析式________________(答案不唯一)
(13)已知
，那么
=
（14）若存在常数p>0，使得函数f(x)满足
（x∈R），则f(x)的一个正周期为_____________
（15）设
为实数，函数
，
（I）讨论的奇偶性； （II）求的最小值。
(16)．（本小题满分14分）
已知定义在上的函数满足：
，当
时，
。
（Ⅰ）求证：为奇函数；
（Ⅱ）求证：为上的增函数；
（Ⅲ）解关于的不等式： 
(17)．（满分13分）
设函数
（1）求导数
（2）对于（1）中
，若不等式
成立，求a的取值范围.
ADDACACBBB 11. 17 12. 
（答案不唯一） 13
14
注：填的正整数倍中的任何一个都正确
15本小题主要考查函数的概念、函数的奇偶性和最小值等基础知识，考查分类讨论的思想和逻辑思维能力.满分12分.
解：（Ⅰ）当
为偶函数.
………………2分
当
.
此时函数既不是奇函数，也不是偶函数. ………………4分
（Ⅱ）（i）当
若
上单调递减，从而，函数
上的最小值为
若
，则函数
上的最小值为
………7分
（ii）当
时，函数
若
若
……………10分
综上，当
当
当
16．解：（1）因，
令
得
，即
；………………………1分
再令
即
得
，
，
为奇函数……………………………………………3分
（2）设
、
，且
，
，由已知得
。……4分
，………………………6分
为上的增函数；……………………………………7分.
（3）
……………………8分.
故原不等式化为：
，
即
… ………………………………………9分
，…………………………………………10分
又为上的增函数；
，即
，
…………………11分
当
，即
时，不等式的解集为
；……12分
当
，即
时，不等式的解集为
；………………13分
当
，即
时，不等式的解集为
………14分
17．解：（1）∵函数
∴
…………2分
令
则
…………4分
∴
有两个不相同的实数根 
）
则当
∴有两个不同的极值点
处取得极大值，在x2处取得极小值.……6分
（2）∵
的两个根
∴
……………………7分
∴
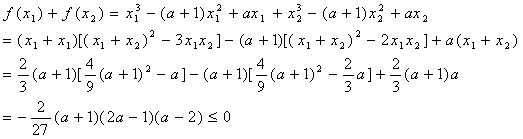
………………12分
又∵a>1 ∴a≥2 ………………13分