函数练习卷
一、选择题(本大题共12小题,每小题5分,共60分)
1.集合![]() =
=
A.![]() B.{1} C.{0,1,2} D. {-1,0,1,2}
B.{1} C.{0,1,2} D. {-1,0,1,2}
2.已知集合![]() ,集合B={xx>a},若A∩B=
,集合B={xx>a},若A∩B=![]() ,则a的取值范围是:
,则a的取值范围是:
A.![]() B.a≥1
C.a<1 D.
B.a≥1
C.a<1 D. ![]()
3. 函数![]() 的定义域为
的定义域为
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
 4.函数
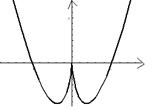
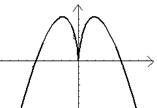
4.函数![]() 的图像是:
的图像是:
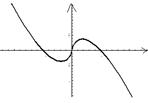
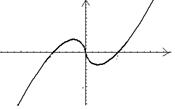
A B C D
5.函数![]() 是:
是:
A.奇函数,且在![]() 上是增函数
B.奇函数,且在
上是增函数
B.奇函数,且在![]() 上是减函数
上是减函数
C.偶函数,且在![]() 上是增函数
D.偶函数,且在
上是增函数
D.偶函数,且在![]() 上是减函数
上是减函数
6.设![]() ,则
,则![]() 的大小关系是:
的大小关系是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数![]() 的值域是:
的值域是:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.设a1、b1、c1、a2、b2、c2均为非零实数,不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为集合M和N,那么“![]() ”是“M=N”的
”是“M=N”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
9.设![]() 是方程
是方程![]() 的解,则
的解,则![]() 在下列哪个区间内:
在下列哪个区间内:
A.(3,4) B.(2,3) C.(1,2) D.(0,1)
10.已知![]() (
(![]() 是常数),在
是常数),在![]() 上有最大值3,那么在
上有最大值3,那么在![]() 上的最小值是
上的最小值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(每题5分,共20分,其中15题第一空2分,第二空3分)
|
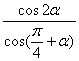 值为
.
值为
.
12.如图,函数![]() 的图象在点P处的切线方程是
的图象在点P处的切线方程是
![]() ,则
,则![]() =
.
=
.
13.函数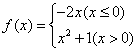 ,则
,则![]() ;若
;若![]() ,则x=
。
,则x=
。
14. 一种放射性物质不断变化为其他物质,每经过一年剩留的质量约是原来的75%,估计约经过 年,该物质的剩留量是原来的![]() (结果保留1个有效数字)(
(结果保留1个有效数字)(![]() ,
,![]() )
)
三、解答题(本大题共6小题,共80分.)
15. 设![]() 为奇函数,
为奇函数,![]() 为常数.
为常数.
(1) 求![]() 的值;
的值;
(2) 证明![]() 在区间(1,+∞)内单调递增;
在区间(1,+∞)内单调递增;
(3) 若对于区间[3,4]上的每一个![]() 的值,不等式
的值,不等式![]() >
>![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
16.(本小题满分14分)
已知函数![]() .
.
(Ⅰ)将![]() 化简成
化简成![]()
![]() (其中
(其中![]() )的形式;
)的形式;
(Ⅱ)利用“五点法”画出函数![]() 在一个周期内的简图.(要求先列表,然后在答题卷给出的平面直角坐标系内画图)
在一个周期内的简图.(要求先列表,然后在答题卷给出的平面直角坐标系内画图)
17.(本小题满分14分)
已知函数![]()
![]() 满足条件:①
满足条件:①![]() ;②对一切
;②对一切![]() ,都有
,都有![]() .
.
(Ⅰ)求![]() 、
、![]() 的值;
的值;
(Ⅱ)是否存在实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 上有最小值-5?若存在,请求出实数
上有最小值-5?若存在,请求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
18.已知△ABC的面积S满足![]() ,且满足
,且满足![]() 。
。
(1)求∠B的取值范围。
(2)若![]() 与
与![]() 的夹角为
的夹角为![]() ,求
,求![]() 的最小值。
的最小值。
19.(本题满分12分)
已知![]()
(1)当a=1时,求![]() 的单调区间;
的单调区间;
(2)是否存在实数a,使![]() 的极大值为3?若存在,求出a的值,若不存在,说明理由.
的极大值为3?若存在,求出a的值,若不存在,说明理由.