高考数学递推数列求通项题型分类归纳解析
类型1 ![]()
解法:把原递推公式转化为![]() ,利用累加法(逐差相加法)求解。
,利用累加法(逐差相加法)求解。
例1:已知数列![]() 满足
满足![]() ,
,![]() ,求
,求![]() 。
。
解:由条件知:![]()
分别令![]() ,代入上式得
,代入上式得![]() 个等式累加之,即
个等式累加之,即![]()
![]() 所以
所以![]()
![]() ,
,![]()
类型2 ![]()
解法:把原递推公式转化为![]() ,利用累乘法(逐商相乘法)求解。
,利用累乘法(逐商相乘法)求解。
例2:已知数列![]() 满足
满足![]() ,
,![]() ,求
,求![]() 。
。
解:由条件知![]() ,分别令
,分别令![]() ,代入上式得
,代入上式得![]() 个等式累乘之,即
个等式累乘之,即![]()
![]()
![]()
又![]() ,
,![]()
例3:已知![]() ,
,![]()
![]() ,求
,求![]() 。
。
解:![]()
![]() 。
。
变式:(2004,全国I,理15.)已知数列{an},满足a1=1,![]() (n≥2),则{an}的通项
(n≥2),则{an}的通项![]()
![]()
解:由已知,得![]() ,用此式减去已知式,得
,用此式减去已知式,得
当![]() 时,
时,![]() ,即
,即![]() ,又
,又![]() ,
,
![]() ,将以上n个式子相乘,得
,将以上n个式子相乘,得![]()
![]()
类型3 ![]() (其中p,q均为常数,
(其中p,q均为常数,![]() )。
)。
解法(待定系数法):把原递推公式转化为:![]() ,其中
,其中![]() ,再利用换元法转化为等比数列求解。
,再利用换元法转化为等比数列求解。
例4:已知数列![]() 中,
中,![]() ,
,![]() ,求
,求![]() .
.
解:设递推公式![]() 可以转化为
可以转化为![]() 即
即![]() .故递推公式为
.故递推公式为![]() ,令
,令![]() ,则
,则![]() ,且
,且![]() .所以
.所以![]() 是以
是以![]() 为首项,2为公比的等比数列,则
为首项,2为公比的等比数列,则![]() ,所以
,所以![]() .
.
变式:(2006,重庆,文,14)
在数列![]() 中,若
中,若![]() ,则该数列的通项
,则该数列的通项![]()
![]() _______________
_______________
(key:![]() )
)
类型4 ![]() (其中p,q均为常数,
(其中p,q均为常数,![]() )。 (或
)。 (或![]() ,其中p,q, r均为常数)
。
,其中p,q, r均为常数)
。
解法:一般地,要先在原递推公式两边同除以![]() ,得:
,得:![]() 引入辅助数列
引入辅助数列![]() (其中
(其中![]() ),得:
),得:![]() 再待定系数法解决。
再待定系数法解决。
例5:已知数列![]() 中,
中,![]() ,
,![]() ,求
,求![]() 。
。
解:在![]() 两边乘以
两边乘以![]() 得:
得:![]()
令![]() ,则
,则![]() ,解之得:
,解之得:![]()
所以![]()
类型5 递推公式为![]() (其中p,q均为常数)。
(其中p,q均为常数)。
解 (特征根法):对于由递推公式![]() ,
,![]() 给出的数列
给出的数列![]() ,方程
,方程![]() ,叫做数列
,叫做数列![]() 的特征方程。若
的特征方程。若![]() 是特征方程的两个根,当
是特征方程的两个根,当![]() 时,数列
时,数列![]() 的通项为
的通项为![]() ,其中A,B由
,其中A,B由![]() 决定(即把
决定(即把![]() 和
和![]() ,代入
,代入![]() ,得到关于A、B的方程组);当
,得到关于A、B的方程组);当![]() 时,数列
时,数列![]() 的通项为
的通项为![]() ,其中A,B由
,其中A,B由![]() 决定(即把
决定(即把![]() 和
和![]() ,代入
,代入![]() ,得到关于A、B的方程组)。
,得到关于A、B的方程组)。
例6: 数列![]() :
:![]() ,
, ![]() ,求
,求![]()
解(特征根法):的特征方程是:![]() 。
。![]() ,
,
![]()
![]()
![]() 。又由
。又由![]() ,于是
,于是
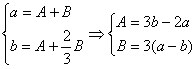 故
故![]()
练习:已知数列![]() 中,
中,![]() ,
,![]() ,
,![]() ,求
,求![]() 。
。
![]() 。
。
变式:(2006,福建,文,22)
已知数列![]() 满足
满足![]() 求数列
求数列![]() 的通项公式;
的通项公式;
(I)解: ![]()
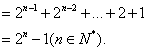
类型6 递推公式为![]() 与
与![]() 的关系式。(或
的关系式。(或![]() )
)
解法:利用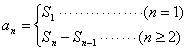 与
与![]() 消去
消去![]()
![]() 或与
或与![]()
![]() 消去
消去![]() 进行求解。
进行求解。
例7:数列![]() 前n项和
前n项和![]() .(1)求
.(1)求![]() 与
与![]() 的关系;(2)求通项公式
的关系;(2)求通项公式![]() .
.
解:(1)由![]() 得:
得:![]()
于是![]()
所以![]()
![]() .
.
(2)应用类型4(![]() (其中p,q均为常数,
(其中p,q均为常数,![]() ))的方法,上式两边同乘以
))的方法,上式两边同乘以![]() 得:
得:![]()
由![]() .于是数列
.于是数列![]() 是以2为首项,2为公差的等差数列,所以
是以2为首项,2为公差的等差数列,所以![]()
![]()
类型7 ![]()
![]()
解法:这种类型一般是等式两边取对数后转化为![]() ,再利用待定系数法求解。
,再利用待定系数法求解。
例8:已知数列{![]() }中,
}中,![]()
![]() ,求数列
,求数列![]()
解:由![]() 两边取对数得
两边取对数得![]() ,
,
令![]() ,则
,则![]() ,再利用待定系数法解得:
,再利用待定系数法解得:![]() 。
。
类型8 ![]()
解法:这种类型一般是等式两边取倒数后换元转化为![]() 。
。
例9:已知数列{an}满足:![]() ,求数列{an}的通项公式。
,求数列{an}的通项公式。
解:取倒数:![]()
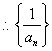 是等差数列,
是等差数列,![]()
![]()
![]()
变式:(2006,江西,理,22)
已知数列{an}满足:a1=![]() ,且an=
,且an=![]() 求数列{an}的通项公式;
求数列{an}的通项公式;
解:(1)将条件变为:1-![]() =
=![]() ,因此{1-
,因此{1-![]() }为一个等比数列,其首项为1-
}为一个等比数列,其首项为1-![]() =
=![]() ,公比
,公比![]() ,从而1-
,从而1-![]() =
=![]() ,据此得an=
,据此得an=![]() (n³1)
(n³1)
类型9周期型
解法:由递推式计算出前几项,寻找周期。
例10:若数列![]() 满足
满足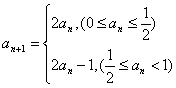 ,若
,若![]() ,则
,则![]() 的值为___________。
的值为___________。
变式:(2005,湖南,文,5)
已知数列![]() 满足
满足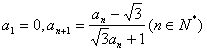 ,则
,则![]() = ( )
= ( )
A.0 B.![]() C.
C.![]() D.
D.![]()