08高考数学（文科）第二次月考
数学试题（文科）
一、选择题（5分/题×10=50分）http://www.mathedu.cn中国数学教育网
1．设
，则M－N等于（ ）
A．{4，5，6，7，8，9，10} B．{7，8}
C．{4，5，6，9，10} D．{4，5，6}
2．不等式
的解集是http://www.mathedu.cn中国数学教育网
（ ）
A．（－1，3） B．（－3，1）∪（3，7）
C．（－7，－3） D．（－7，－3）∪（－1，3）
3．函数
的反函数的解析表达式为 （ ）
A．
B．
C．
D．
4．函数
的图象过定点 （ ）
A．（0，
） B．（0，1） C．（1，0） D．（，0）
5．已知命题p:a=0，命题q:ab=0，则p是q的 （ ）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．即不充分也不必要条件
6．等差数列{an}的公差为d，前n项的和为Sn，当首项a1与d变化时，a2+ a8+a11是一个定值，则下列各数中也为定值的是 （ ）
A．S15 B．S13 C．S8 D．S7
7．若数列
满足
，则该数列中相邻两项的积为负数的是
（ ）
A．
B．
C．
D．
8．已知数列{an}是等比数列，且每一项都是正数，若a2，a48是
的两个根，则
的值为 （ ）
A．
B．
C．
D．35
9．使关于x的不等式
有解的实数k的取值范围是 （ ）
A．
B．（－
，＋1） C．（－1，+） D．（1，+）
|
是以3为周期的奇函数，且
，则 （ ）
A．a>1 B．a <－1 C．a >2 D．a <－2
二、填空题（5分/题×5=25分）
11．若等差数列{an}中，公差d=2，且
的值是
12．
13．若函数
在闭区间[－3，0]上的最大值，最小值分别为M，m，则M+m=
14．已知函数
在R上存在反函数，且函数的图象过点（1，2），那么
的反函数的图象一定经过点
15．设是定义在R上的函数，给定下列三个条件：（1）是偶函数；（2）的图象关于直线x=1对称；（3）T=2为的一个周期。如果将上面（1）、（2）、（3）中的任意两个作为条件，余下一个作为结论，那么构成的三个命题中真命题的个数有
个
三、解答题（共计75分）
16．（12分）记函数
的定义域为集合M，函数
的定义域为集合N。求：（Ⅰ）集合M，N；（Ⅱ）集合M∩N，M∪N。
17．（12分）已知函数
的图象关于原点对称，且
。
（1）求函数
的表达式；（2）解不等式
18．（12分）已知二次方程
（1）若方程的两根
，求实数a的取值范围；（2）若两根都小于－1，求a的取值范围。
19．（12分）数列的前n项和Sn，且
，求：
（Ⅰ）
的值及数列的通项公式；
（Ⅱ）
的值.
20．（13分）设数列满足：
，（n=1，2，…）。
（1）令
，（n=1，2，…）。求数列
的通项公式；（2）求数列
的前n项和Sn。
21．（14分）函数
为常数）是奇函数。（1）求实数m的值和函数
的图象与横轴的交点坐标。（2）设
，求的最大值F（t）；（3）求F（t）的最小值。
参考答案
一、选择题
1.D 2.D 3.C 4.C 5.B 6.B 7.A 8.A 9.B 10.B
|
11．120 12．2 13．－14 14．（2，5） 15．3
三、解答题
16．（1）
（2）
17．（1）
（2）
18．（1）
（2）
19．（1）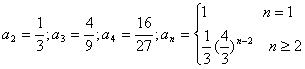
（2）
20．（1）
（2）
所以 
则
得到
21．解：（1）由于为奇函数，易得m=0
设
①当3t<0时，上述方程只有一个实数根x=0，所以与x轴的交点坐标为（0，0）
②当3t=0时，上述方程有三个相等实数根x=0，所以与x轴的交点坐标为（0，0）
③当3t>0时，上述方程的解为x1=0，x2，x 3=
，所以与横轴的交点坐标分别为（0，0），（
，0），（－，0）
（2）显然
是偶函数，
所以只要求出的最大值即可
又
①
为增函数， ∴
∴
②t>0时，则在[0，1]上
（i）
即
时，则在[0，1]上为减函数
∴
，
故
（ii）0<t<1时，则在[0，1]上
| x | 0 | （0， |
| （ | 1 |
|
| — | 0 | + | ||
|
| 0 | ↓ | 极小值 －2t | ↑ | 1－3t |
）
所以可以画出的草图如下，并且由图可知：
（10）当
（20）当
…
|
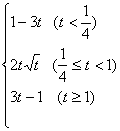
（3）显然
上为减函数，
在
上为增函数，
即在
为增函数