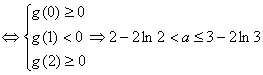08高考数学（理科）第二次月考
数学试题（理科）
一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。http://www.mathedu.cn中国数学教育网
1．已知集合I={1，2，3，4}，A={1}，B={2，4}，则
（ ）
A．{1} B．{1，3} C．{3} D．{1，2，3}
2．若集合A={1，m2}，B={2，4}，则“m=2”是“A∩B={4}”的 （ ）
A．充要条件 B．充分不必要条件
C．必要不充分条件 D．既不充分也不必要条件
3．曲线
处的切线与坐标轴所围三角形的面积为 （ ）
A．
B．
C．
D．
4．设
为可导函数，且
，则曲线
在点
处的切线的斜率是http://www.mathedu.cn中国数学教育网 （ ）
A．－2 B．－1 C．
D．2
5．设函数
的反函数为
（ ）
A．－2 B．－1 C．1 D．2
|
的图象如图所示，则当0<a<1时，函数
的单调区间是 （ ）
A．
B．
C．
D．
7．函数
的单调减区间为 （ ）
A．
B．
C．
D．（3，+ 
）
8．设函数定义在实数集上，它的图象关于直线x=1对称，且当
时，
，
则有 （ ）
A．
B．
C．
D．
9．设
，则下列关系式中一定成立的是（ ）
A．
B．
C．
D．
|
的值域为[1，9]，则
的取值范围是 （ ）
A．[2，4] B．[4，12] C．[2，2
] D．[4，16]
二、填空题：本大题共5小题，每小题5分，把答案填在题中横线上。
11．设函数
=
12．不等式
的解集是
13．已知函数
=
14．当
时，不等式
恒成立，则a的取值范围是
15．对于函数定义域中任意的
，有如下结论：
①
②
③
④
当
时，上述结论中正确结论的序号是
三、解答题：本大题共5小题，共75分，解答题应写出文字说明，证明过程或演算步骤。
16．（本小题满分12分）
已知函数
的定义域是集合A，函数
的定义域是集合B。
（1）求集合A，B；（2）若
，求实数a的取值范围。
17．（本小题满分12分）
|
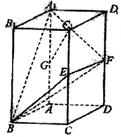
（1）求证：A1F⊥面BEF；
（2）求证GC1//面BEF；
（3）求直线A1B与平面BEF所成的角。
18．（本小题满分12分）
对于函数
若存在
，使
成立，则称
为的不动点，已知函数
（1）当a=1，b=3时，求函数的不动点；
（2）若对于任意实数b，函数恒有两个相异的不动点，求a的取值范围。
19．（本小题满分12分）
设
有最小值－8。
（1）求a，b；
（2）求满足
的集合A；
（3）若非空集合
，求实数m的取值范围。
20．（本小题满分13分）
已知函数
的图象过（－1，1）点，其反函数
的图象过（8，2）点。
（1）求a，k的值；
（2）若将的图象向在平移两个单位，再向上平移1个单位，就得到函数
的图象，写出的解析式；
（3）若函数
的最小值及取最小值时x的值。
21．（本小题满分14分）
设函数
（1）求的单调增区间和单调减区间；
（2）若当
时（其中e=2.71828…），不等式
恒成立，求实数m的取值范围；
（3）若关于x的方程
上恰有两个相异的实根，求实数a的取值范围。
参考答案
一、选择题
1—5 BBCAA 6—10 DDCCB
|
11．
12．（－1，0） 13．7 14．
15．②③
三、解答题：
16．（本小题满分12分）
解：（1）由
得 
由 
得
∴
（2）∵
∴
17．（本小题满分12分）
证明：（1）略 （2）略
（3）在Rt△A1FB中， A1F=
∴
，所以直线A1B与平面BEF所成的角为arcsin
18．（本小题满分12分）
解：（2）a=1，b=3时，由
∴不动点为－1和－2
（2）由题意知，
有两不等实根
∴
恒成立（对任意实数b）
∴
19．（本小题满分12分）
解：（1）
∵
∴
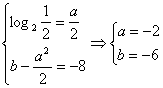
（2）
∴
（3）∵
∴m>0 
∵
又1+m>1>0 ∴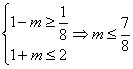
∴
20．（本小满分13分）
解：（1）由题意知
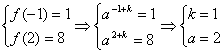
（2）由（1）知
∴
∴
（x>－2）
（3）
∵
∴
∴
当且仅当 
21．（本小题满分14分）
解：（1）函数定义域为
∵
由
∴增区间：（0，+∞），减区间：（－1，0）
（2）由
∵
∴
∴
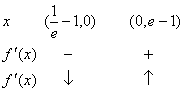
时，恒成立。
（3）
∵
由
，
故
上恰有两相异实根
