08高考数学第一次教学质量检测数学(理)
一、选择题:本大题共11小题,每小题5分,共55分。
 1.复数
1.复数![]() A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
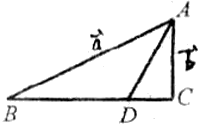
2.如图,已知![]() ,用
,用![]() 表示
表示![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知角![]() 在第一象限且
在第一象限且![]() ,则
,则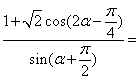
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.把直线![]() 按向量
按向量![]() 平移后恰与
平移后恰与![]() 相切,则实数
相切,则实数![]() 的值为
的值为
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
5.等比数列![]() 中,“
中,“![]() ”是“
”是“![]() ”的
”的
A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分又不必要条件
 6.已知
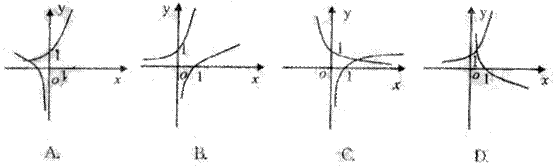
6.已知![]() ,函数
,函数![]() 与函数
与函数![]() 的图象可能是
的图象可能是
7.已知双曲线![]() 满足彖件:(1)焦点为
满足彖件:(1)焦点为![]() ;(2)离心率为
;(2)离心率为![]() ,求得双曲线
,求得双曲线![]() 的方程为
的方程为![]() 。若去掉条件(2),另加一个条件求得双曲线
。若去掉条件(2),另加一个条件求得双曲线![]() 的方程仍为
的方程仍为![]() ,则下列四个条件中,符合添加的条件共有
,则下列四个条件中,符合添加的条件共有
①双曲线![]() 上的任意点
上的任意点![]() 都满足
都满足![]() ;
;
②双曲线![]() 的—条准线为
的—条准线为![]()
③双曲线![]() 上的点
上的点![]() 到左焦点的距离与到右准线的距离比为
到左焦点的距离与到右准线的距离比为![]()
④双曲线![]() 的渐近线方程为
的渐近线方程为![]()
A.1个 B.2个 C.3个 D.4个
8.设偶函数![]() 在
在![]() 上单调递增,则
上单调递增,则![]() 与
与![]() 的大小关系是
的大小关系是
A.![]() B.
B.![]() C.
C.![]() D.不能确定
D.不能确定
9.有两排座位,前排4个座位,后排5个座位,现安排2人就坐,并且这2人不相邻(一前一后也视为不相邻),那么不同坐法的种数是
A.18 B.26 C.29 D.58
10.若二面角![]() 为
为![]() ,直线
,直线![]() ,直线
,直线![]() ,则直线
,则直线![]() 与
与![]() 所成的角取值范围是
所成的角取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.集合![]() ,集合
,集合![]() 。先后掷两颗骰子,设掷第—颗骰子得点数记作
。先后掷两颗骰子,设掷第—颗骰子得点数记作![]() ,掷第二颗骰子得点数记作
,掷第二颗骰子得点数记作![]() ,则
,则![]() 的概率等于
的概率等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:(共4题.每题4分,满分16分)
12.若![]() 的展开式中各项系数的和为729,则展开式中
的展开式中各项系数的和为729,则展开式中![]() 项的系数是
项的系数是
13.关于![]() 的不等式
的不等式![]() 的解集为
的解集为
14.已知函数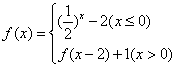 ,则
,则![]()
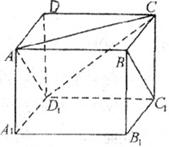 15.如图,正方体
15.如图,正方体![]() ,则下列四个命题:
,则下列四个命题:
①![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 的体积不变;
的体积不变;
②![]() 在直线
在直线![]() 上运动时,直线AP与平面ACD1所成角的大小不变;
上运动时,直线AP与平面ACD1所成角的大小不变;
③![]() 在直线
在直线![]() 上运动时,二面角
上运动时,二面角![]() 的大小不变;
的大小不变;
④M是平面![]() 上到点D和
上到点D和![]() 距离相等的点,则M点的轨迹是过
距离相等的点,则M点的轨迹是过![]() 点的直线
点的直线
其中真命题的编号是 (写出所有真命题的编号)
三、解答题(共6题,满分79分)
16.(12分)已知函数![]()
(1)求函数![]() 的周期、对称轴方程;(2)求函数
的周期、对称轴方程;(2)求函数![]() 单调增区间。
单调增区间。
17.(14分)如图,在几何体![]() 中,面
中,面![]() 为矩形,
为矩形,![]() 面
面![]() ,
,![]()
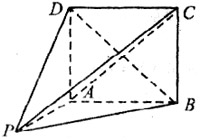 (1)求证;当
(1)求证;当![]() 时,平面PBD⊥平面PAC;
时,平面PBD⊥平面PAC;
(2)当![]() 时,求二面角
时,求二面角![]() 的取值范围。
的取值范围。
18.(12分)设向量![]() ,过定点
,过定点![]() ,以
,以![]() 方向向量的直线与经过点
方向向量的直线与经过点![]() ,以向量
,以向量![]() 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中![]()
(1)求点P的轨迹C的方程;
(2)设过![]() 的直线
的直线![]() 与C交于两个不同点M、N,求
与C交于两个不同点M、N,求![]() 的取值范围
的取值范围
19.(13分)食品监管部门要对某品牌食品四项质量指标在进入市场前进行严格的检测,并规定四项指标中只要第四项不合格或其它三项指标中只要有两项不合格,这种品牌的食品就不能上市。巳知每项指标检测是相互独立的。若第四项不合格的概率为![]() ,且其它三项指标出现不合格的概率均是
,且其它三项指标出现不合格的概率均是![]()
(1)求该品牌的食品能上市的概率;
(2)生产厂方规定:若四项指标均合格,每位职工可得质量保证奖1500元;若第一、第二、第三项指标中仅有一项不合格且第四项指标合格,每位职工可得质量保证奖500元;若该品牌的食品不能上市,每位职工将被扣除质量保证金1000元。设随机变量![]() 表示某位职工所得质量保证奖金数,求
表示某位职工所得质量保证奖金数,求![]() 的期望。
的期望。
20.(14分)已知数列![]() 中,
中,![]()
(1)求证:数列![]() 与
与![]() 都是等比数列;(2)求数列
都是等比数列;(2)求数列![]() 前
前![]() 的和
的和![]() ;
;
(3)若数列![]() 前
前![]() 的和为
的和为![]() ,不等式
,不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的最大值。
的最大值。
21.(14分)已知函数![]() 的定义域为
的定义域为![]() 。
。
(1)求证:直线![]() (其中
(其中![]() )不是函数
)不是函数![]() 图像的切线;
图像的切线;
(2)判断![]() 在
在![]() 上单调性,并证明;
上单调性,并证明;
(3)已知常数![]() 满足
满足![]() ,求关于
,求关于![]() 的不等式
的不等式![]() 的解集
的解集
数学试题(理)参考答案及评分标准
ABCCC BBC DCB 12.![]() 13.
13.![]() 14.1004 15.①③④
14.1004 15.①③④
16.![]() 3分
3分
(1)![]() 的周期
的周期![]() ,函数
,函数![]() 对称轴方程为
对称轴方程为![]() ; 6分
; 6分
(2)由![]() 得
得![]()
∴求函数![]() 单调增区间为
单调增区间为![]() 。 12分
。 12分
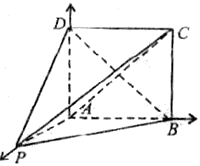 17.以A为坐标原点,射线AP、AB、AD分别为x轴、y轴、z轴的正半轴建立如图所示的坐标系。设
17.以A为坐标原点,射线AP、AB、AD分别为x轴、y轴、z轴的正半轴建立如图所示的坐标系。设![]() ,由已知得
,由已知得![]()
(1)当![]() 时,
时,![]() ,
,
∴![]() 4分
4分
∴![]() ,∴
,∴![]()
又![]() ,∴平面PBD⊥平面PAC; 6分
,∴平面PBD⊥平面PAC; 6分
解法二:当![]() 时,矩形
时,矩形![]() 为正方形,∴
为正方形,∴![]()
∵![]() 面
面![]() ,∴
,∴![]() 2分
2分
又![]() ,∴BD⊥平面PAC,BD
,∴BD⊥平面PAC,BD![]() 平面PBD,∴平面PBD⊥平面PAC
平面PBD,∴平面PBD⊥平面PAC
(2)由![]()
得![]()
设![]() 平面PDC,∴
平面PDC,∴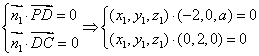
∴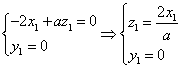 不妨设
不妨设![]() ,则
,则![]()
设![]() 平面PDB,∴
平面PDB,∴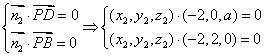
∴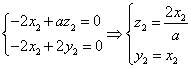 不妨设
不妨设![]() ,则
,则![]() 10分
10分
∴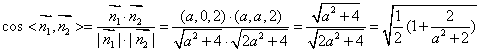
当![]() 变化时,即
变化时,即![]() ,
,![]()
![]() 12分
12分
又![]() ,∴
,∴![]() 14分
14分
18.(1)设![]() ∵
∵![]() ,
,
∴![]() ,
,![]() 2分
2分
过定点![]() ,以
,以![]() 方向向量的直线方程为:
方向向量的直线方程为:![]()
过定点![]() ,以
,以![]() 方向向量的直线方程为:
方向向量的直线方程为:![]()
联立消去![]() 得:
得:![]() ∴求点P的轨迹C的方程为
∴求点P的轨迹C的方程为![]() 6分
6分
(2)当过![]() 的直线
的直线![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 与曲线
与曲线![]() 无交点,不合题意,
无交点,不合题意,
∴设直线![]() 的方程为:
的方程为:![]() ,
,![]() 与曲线
与曲线![]() 交于
交于![]()
由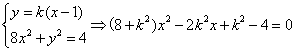
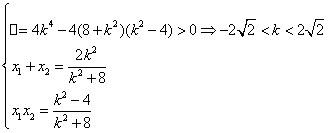
![]()
∴![]()
![]()
![]() ∵
∵![]() ,∴
,∴![]() 的取值范围是
的取值范围是![]() 12分
12分
19.(1)该品牌的食品能上市的概率等于1减去该品牌的食品不能上市的概率,
即![]() 6分
6分
解法二:该品牌的食品能上市的概率等于四项指标都合格或第一、第二、第三项指标中仅有一项不合格且第四项指标合格的概率,即![]()
(2)![]() ;
;
易知![]() 12分
12分
∴![]() 的分布列为:
的分布列为:
|
| 1500 | 500 |
|
|
|
|
|
|
∴![]() 的期望为
的期望为![]() 13分
13分
20.(1)∵![]() ,∴
,∴![]() 2分
2分
∴数列![]() 是以1为首项,
是以1为首项,![]() 为公比的等比数列;
为公比的等比数列;
数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列。 4分
为公比的等比数列。 4分
(2)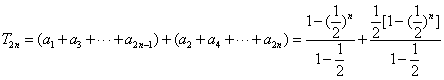
![]() 9分
9分
(3)![]()
![]() 当且仅当
当且仅当![]() 时取等号,所以
时取等号,所以![]() ,即
,即![]() ,∴
,∴![]() 的最大值为
的最大值为![]()
21.(1)![]() 2分
2分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 而
而![]() 在
在![]() 连续,∴
连续,∴![]() 在
在![]() 上是减函数,又
上是减函数,又![]()
∴函数![]() 图像上任意点处切线斜率
图像上任意点处切线斜率![]() 存在并满足
存在并满足![]() 4分
4分
当![]() 时,直线
时,直线![]() 斜率不存在,∴直线
斜率不存在,∴直线![]() 不是函数
不是函数![]() 图像的切线;当
图像的切线;当![]() 时,直线
时,直线![]() 斜率
斜率![]() ,则
,则![]() ,∴直线
,∴直线![]() 不是函数
不是函数![]() 图像的切线 6分
图像的切线 6分
已知函数![]() 的定义域为
的定义域为![]() 。
。
(2)由(1)易知![]() 在
在![]() 上是减函数,而
上是减函数,而![]() ,当
,当![]() 时,
时,![]() ,而
,而![]() 在
在![]() 上连续,∴
上连续,∴![]() 在
在![]() 上是减函数 10分
上是减函数 10分
(3)∵![]() 在
在![]() 上是减函数,并且
上是减函数,并且![]() 在
在![]() 上是偶函数
上是偶函数
由不等式![]()
等价于![]()
∵![]() ,
,![]()
∴![]() ,
,
即![]() ,∴
,∴![]()
当![]() 时,
时,![]() ,此时原不等式解集为
,此时原不等式解集为![]()
当![]() 时,原不等式解集为
时,原不等式解集为![]()
当![]() 时,
时,![]() ,此时原不等式解集为
,此时原不等式解集为![]()
14分