08高考数学第一次模拟测试
2008.3.21
一:填空题(每题5分,共70分)
|
2、当x = 3时,右面算法输出的结果是 。
3、已知双曲线![]() 的一条渐近线方程为y = x,
的一条渐近线方程为y = x,
则实数m= 。
4、在复平面内,复数z=![]() 对应的点位于第
象限。
对应的点位于第
象限。
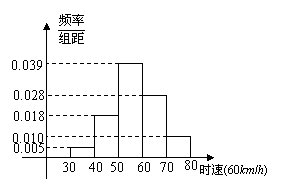
5、有100辆汽车在一个时段经过某一雷达测速区,这些汽车运行时速的频率分布直方图如图所示,则时速超过60km/h的汽车数量约为 辆。
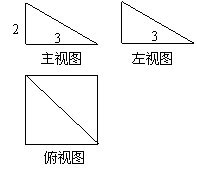
 6、一个几何体的三视图如图所示,则它的体积V= 。
6、一个几何体的三视图如图所示,则它的体积V= 。
7、设直线x = m分别交函数y = sinx、y = sin(x+![]() )的图象于M、N两点,则M、N距离的最大值为 。
)的图象于M、N两点,则M、N距离的最大值为 。
8、在正三棱锥P – ABC中,D、E分别是AB、BC的中点,有下列三个结论:
(1)AC⊥PB;(2)AC∥平面PDE;(3)AB⊥平面PDE。
则所有正确结论的序号是 。
9、已知向量![]() ,向量
,向量![]() 满足
满足![]() ∥
∥![]() ,
,![]() =1, 则
=1, 则![]() =
。
=
。
10、已知曲线y =![]() 上一点P(1, e)处的切线分别交x轴、y轴于A、B两点,O为原点,则ΔOAB的面积为 .
上一点P(1, e)处的切线分别交x轴、y轴于A、B两点,O为原点,则ΔOAB的面积为 .
11、有一个质地均匀的正四面体,它的四个面上分别标有1,2,3,4这四个数字。现将
它连续抛掷3次,其底面落于桌面,记三次在正四面体底面的数字和为S,则“S恰好为4”的概率为 。
12、设S n表示等比数列{a n }(n∈N*)的前n项和,已知![]() =3,则
=3,则![]() = 。
= 。
|
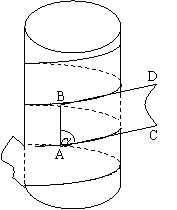 |
则这个式子为 。
14、水管或煤气管的外部经常需要包扎,已便对管道起保护
作用,包扎时用很长的带子缠绕在管道外部。若要使带子
全部包住管道且没有重叠的部分(不考虑管子两端的情况,
如图所示),这就要精确计算带子的“缠绕角度”
![]() (
(![]()
指缠绕中将部分带子拉成图中所示的平面ABCD时的∠ABC,其中AB为管道侧面
母线的一部分)。若带子宽度为1,水管直径为2,则“缠绕角度”![]() 的余弦值为 。
的余弦值为 。
二:解答题
15、(本题满分14分)
在ΔABC中,已知a、b、c分别是角A、B、C的对边,不等式x 2cosC + 4xsinC + 6≥0对一切实数x恒成立。
(1)求角C的最大值;
(2)若角C取得最大值,且a = 2b,求角B的大小。
16、(本题满分14分)
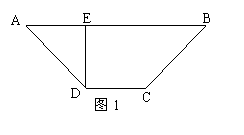
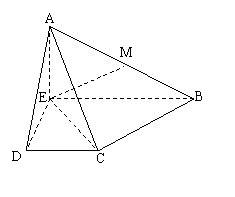
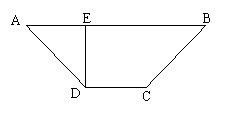
已知四边形ABCD是等腰梯形,AB=3,DC=1,∠BAD=45o,DE⊥AB(如图1)。现将ΔADE沿DE折起,使得AE⊥EB(如图2),连接AC,AB,设M是AB的中点。
(1)求证:BC⊥平面AEC;
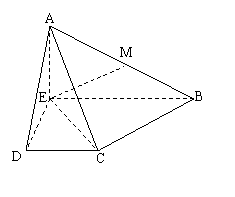 (2)判断直线EM是否平行平面ACD,并说明理由。
(2)判断直线EM是否平行平面ACD,并说明理由。
 | |||
| |||
17、(本题满分15分)
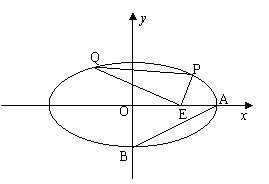 已知中心在原点O,焦点在x轴上的椭圆C的离心率为
已知中心在原点O,焦点在x轴上的椭圆C的离心率为![]() ,点A、B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A、B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为![]() 。
。
(1)求椭圆C的标准方程;
(2)已知点E(3, 0),设点P、Q是椭圆C上的两个动点,
满足EP⊥EQ,求![]() 的取值范围。
的取值范围。
18、(本题满分15分)
在平面直角坐标系中,直线y = –2x + 5上有一系列点:P0 (1, 3), P1 (x1, y1), P2 (x2, y2),
……,P n (x
n , y n),
……,已知数列{![]() }是首项为
}是首项为![]() ,公差为1的等差数列。
,公差为1的等差数列。
(1)求数列{x n} (n∈N*)及数列{y n} (n∈N*)的通项公式;
(2)是否存在一个半径最小的圆C,使得对一切n∈N*,点P n (x n , y n)均在此圆的内部(包括圆周)?若存在,求出此圆的方程;若不存在,请说明理由。
19、(本题满分16分)
某工厂统计资料显示,一种产品次品率p与日产量x (x∈N*, 80≤x≤100)件之间的关系如下表所示:
| 日产量x | 80 | 81 | 82 | … | x | … | 98 | 99 | 100 |
| 次品率p |
|
|
| … | P (x) | … |
|
|
|
其中P (x)= ![]() (a为常数)。已知生产一件正品盈利k元,生产一件次品损失元
(a为常数)。已知生产一件正品盈利k元,生产一件次品损失元![]() (k为给定的常数)。
(k为给定的常数)。
(1)求出a,并将该厂的日盈利额y(元)表示为日生产量x(件)的函数;
(2)为获取最大盈利,该厂的日生产量应定为多少件?
20、(本题满分16分)![]()
已知a为实数,函数f (x) = x 2 – 2 a l n x。
(1)求f (x)在![]() 上的最小值g (a);
上的最小值g (a);
(2)若a > 0,试证明“方程f (x) =2 a x有惟一解”的充要条件是“a=![]() ”。
”。
参考答案
一:填空题
1、{x2<x<4} 2、6 3、4 4、四 5、
38 6、6 7、![]()
8、(1)(2) 9、![]() 或(
或(![]() ) 10、2e 11、
) 10、2e 11、![]() 12、7
12、7
13、(n2 – n +1) + [(n2 –
n +1) +2]+[ (n2 – n +1)
+4]+ … +[(n2 – n +1) +2(n – 1)]= n3 14、![]()
二:解答题
15、解:(1)由条件知,当cosC=0时,不合题意; …………1分
当cosC≠0时,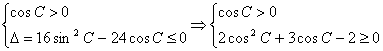 …3分
…3分
所以cosC≥![]() ,因为C为ΔABC的内角,所以0<C≤
,因为C为ΔABC的内角,所以0<C≤![]() ,所以角C的最大值为
,所以角C的最大值为![]() 。…7分
。…7分
(2)由(1)得C=![]() ,所以A+B=
,所以A+B=![]() ,由a = 2b得sinA=2sinB
…………9分
,由a = 2b得sinA=2sinB
…………9分
所以sin(![]() – B)=2sinB,即
– B)=2sinB,即![]() cosB+
cosB+![]() sinB=2sinB,得tanB=
sinB=2sinB,得tanB=![]() …………12分
…………12分
|
 因为B∈(0,
因为B∈(0,
![]() 16、证明:(1)在图1中,
16、证明:(1)在图1中,
过C作CF⊥EB,
|
![]() 所以四边形CDEF是矩形,
所以四边形CDEF是矩形,
|
|
AB=3,所以AE=BF=1,因为∠BAD=45o,
所以DE=CF=1,连接CE,则CE=CB=![]() ,
,
因为EB=2,所以∠BCE=90o。 则BC⊥CE。 …………2分
在图(2)中,因为AE⊥EB,AE⊥ED,EB∩ED=E,所以AE⊥平面BCDE,
因为BC![]() 平面BCDE,所以AE⊥BC, …………4分
平面BCDE,所以AE⊥BC, …………4分
因为AE∩CE=E,所以BC⊥平面AEC;
(2)用反证法:假设EM∥平面ACD,
因为EB∥CD,CD![]() 平面ACD,EB
平面ACD,EB![]() 平面ACD,所以EB∥平面ACD, ………8分
平面ACD,所以EB∥平面ACD, ………8分
因为EB∩EM=E,所以平面AEB∥平面ACD, …………10分
而A∈平面AEB,A![]() 平面ACD,所以假设不成立,
平面ACD,所以假设不成立,
所以EM与平面ACD不平行。 …………14分
17、解:(1)由离心率e=![]() ,得
,得![]() ,所以a = 2b①
………2分
,所以a = 2b①
………2分
因为原点O到直线AB的距离为![]() ,所以
,所以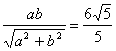 ② …………4分
② …………4分
由①代入②得b2=9,所以a2=36,则椭圆C的标准方程是![]() …………7分
…………7分
(2)因为EP⊥EQ,所以![]() =0,所以
=0,所以![]() …9分
…9分
设P(x , y),则![]() ,即y 2 =9–
,即y 2 =9–![]() ……11分
……11分
所以![]() =
=![]() …13分
…13分
因为–6≤x≤6,所以6≤![]() +6≤81,所以
+6≤81,所以![]() 的取值范围为[6,81]…15分
的取值范围为[6,81]…15分
18、解:(1)由条件得![]() …………2分
…………2分
所以![]() …………4分
…………4分
因为点P n (x n , y n)在直线y = –2x + 5上,
所以![]() …………6分
…………6分
(2)存在一个以P0,P1为直径的圆C,使得对一切n∈N*,点P n (x n , y n)均在此圆的内部(包括圆周),此时圆的方程为(x – 2) 2 + (y – 1) 2 = 5,并且圆的半径最小,…8分
现证明如下:因为![]()
当n=0时,P0D2=5,当n=1时,P1D2=5,
当n≥2时,因为0![]() ≤
≤![]() ,所以PnD2=5(1 –
,所以PnD2=5(1 – ![]() )2<5, ……14分
)2<5, ……14分
由上可得,圆C即为所求的圆。 …………15分
19、解:(1)根据列表数据可得![]() ,
…………2分
,
…………2分
![]()
由题意,当日产量为![]() 时,次品数为
时,次品数为![]() ,正品数为
,正品数为![]() ,……4分
,……4分
![]() 。
…………6分
。
…………6分
整理,得![]() …………8分
…………8分
(2)令![]() 。
。
![]()
![]() …………12分
…………12分
当且仅当![]() ,即
,即![]() 时取得最大盈利,此时
时取得最大盈利,此时![]() 。
…………14分
。
…………14分
答:(1)![]()
(2)为获得最大盈利,该工厂的日生产量应定为96件。 …………15分
20、解:(Ⅰ)![]()
①若![]() ,则
,则![]() ,
,![]() 在
在![]() 上连续,
上连续,
![]() 在
在![]() 上是单调传递增函数。
上是单调传递增函数。
![]() 当
当![]() 时,
时,![]() …………2分
…………2分
②若![]() ,令
,令![]() ,得
,得![]()
当![]() 时,
时,![]() <0, f(x)在
<0, f(x)在![]() 上连续,f (x)在
上连续,f (x)在![]() 上是单调递减函数;
上是单调递减函数;
当![]() 时,
时,![]() >0, f (x)在
>0, f (x)在![]() 上是单调递增函数
上是单调递增函数
则![]() 时,f (x)取得最小值。
时,f (x)取得最小值。
所以, 当a>1, x≥1时,f (x) min = a – ![]() =a – a lna, …………4分
=a – a lna, …………4分
所以![]() …………5分
…………5分
(Ⅱ)记g (x) = f (x) – 2ax = x 2 – 2 a xlnx – 2ax,
![]() ,
,
(1)充分性:若a = ![]() ,则g (x) = x 2 – lnx – x ,
,则g (x) = x 2 – lnx – x ,
![]() …………7分
…………7分
当x∈(0, 1)时,![]() <0, g (x)在(0, 1)上是单调递减函数;
<0, g (x)在(0, 1)上是单调递减函数;
当x∈(1, +∞)时,![]() >0, g (x)在(1, +∞)上是单调递增函数。
>0, g (x)在(1, +∞)上是单调递增函数。
当x=1时,即,当且仅当时取等号。
方程有唯一解,g(x)min=g(1)=0,即![]() 有唯一解。
…………9分
有唯一解。
…………9分
(2)必要性:若方程f(x)=2ax有唯一解,即g(x)=0有唯一解;
令![]() ,得
,得![]()
![]()
![]() (舍去)
(舍去)![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 是单调递减函数;
是单调递减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是单调递增函数。
上是单调递增函数。
当x=x2时, ![]() ,
,![]() …………11分
…………11分
![]() 有唯一解,
有唯一解,![]()
则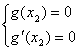 ,即
,即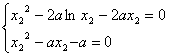 …………12分
…………12分
![]() …………14分
…………14分
设函数![]() ,
,
∵在x>0时, h (x)是增函数,∴h (x) = 0至多有一解。
∵h (1) = 0, ∴方程(*)的解为x 2 = 1,即![]() ,解得
,解得![]() 。
。
由(1)(2)知“方程f (x)
= 2ax有唯一解”的充要条件是“![]() ”
…………16分
”
…………16分