08高考数学第一次诊断性测验科试卷(文理合卷)
(问卷)
(文科:必修+选修Ⅰ;理科:必修+选修Ⅱ)
注意事项:
1.本卷是文理科数学合卷,卷中注明(文科)的 ,理科学生不做;注明(理科)的 ,文科学生不做;未注明的文理科学生都要做.
2.本卷分为问卷(共4页)和答卷(共4页),答案务必书写在答卷的指定位置处.
3.答卷前先将密封线内的项目填写清楚.
4.第Ⅰ卷(选择题,共12小题,共60分),在每小题的四个选项中,只有一项是符合题目要求的.如果选用答题卡,每小题选出答案后,用![]() 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案;如果未选用答题卡请将所选项前的字母代号填写在答卷上.不要答在问卷上.
铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案;如果未选用答题卡请将所选项前的字母代号填写在答卷上.不要答在问卷上.
5. 第Ⅱ卷(非选择题,共10小题,共90分),用钢笔或圆珠笔直接答在问卷中.
第Ⅰ卷 (选择题 共60分)
一、选择题:(共12小题,每小题5分,共60分)
1.(文科)不等式![]() 的解集是
的解集是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理科)复数![]() 的虚部是
的虚部是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.设集合![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.等比数列![]() 中,若
中,若 ![]() ,
,![]() ,则公比
,则公比![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.双曲线![]() 的渐近线与准线的夹角是
的渐近线与准线的夹角是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知直线![]() 和平面
和平面![]() ,则
,则![]() ∥
∥![]() 的一个必要非充分条件是
的一个必要非充分条件是
A. ![]() ∥
∥![]() 、
、![]() ∥
∥![]() B.
B.
![]() ⊥
⊥![]() 、
、![]() ⊥
⊥![]()
C.
![]() ∥
∥![]() 、
、![]()
![]()
![]() D.
D. ![]() 与
与![]() 成等角
成等角
6.若直线![]() 与函数
与函数![]() 的图像分别交于M、N两点,则
的图像分别交于M、N两点,则![]() 的最大值为
的最大值为
A.1 B.![]() C.
C.![]() D.2
D.2
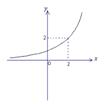
7.在正方体![]() 中,直线
中,直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.将指数函数![]() 的图像按向量
的图像按向量![]() =
=![]() 平移后得到右图,则
平移后得到右图,则![]() =
=
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.对于![]() 上可导的任意函数
上可导的任意函数![]() ,若满足
,若满足![]() ,则必有
,则必有
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.过抛物线![]() 的焦点
的焦点![]() 作斜率为
作斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 、
、![]() 两点,则点
两点,则点![]() 分
分![]() 所成的比值为
所成的比值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11. (文科)某校高一、高二、高三年级的人数之比为![]() ,从中抽取
,从中抽取![]() 名学生作为样本,若每人被抽取的概率是
名学生作为样本,若每人被抽取的概率是![]() ,则该校高三年级的人数为
,则该校高三年级的人数为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(理科)某校![]() 名同龄学生的体重
名同龄学生的体重![]() 服从正态分布
服从正态分布![]() ,
,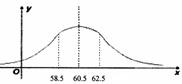 且
且
正态分布的密度曲线如图所示,若![]() ~
~![]()
![]() 体重属于正 常情况, 则这
体重属于正 常情况, 则这![]() 名学生中体重属于正常情况的人数约是(其中
名学生中体重属于正常情况的人数约是(其中
![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.用4种不同的颜色对圆上依次排列的![]() ,
,![]() ,
,![]() ,
,![]() 四点染色,每个点染一种颜色,且相邻两点染不同的颜色,则染色方案的总数为
四点染色,每个点染一种颜色,且相邻两点染不同的颜色,则染色方案的总数为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷
二、填空题(共4小题,每小题5分,共20分)请将答案直接填在问卷的相应表格中.
13.锐角![]() 满足
满足![]() ,则
,则![]() 大小是 .
大小是 .
14.在![]() 的展开式中
的展开式中![]() 的系数是 (用数字作答).
的系数是 (用数字作答).
15.若函数![]()
![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 的取值范围是 .
的取值范围是 .
16.在![]() 中,
中,![]() ,
,![]() ,
,![]() ⊥
⊥![]() 于
于![]() ,
,
若![]() ,则有序实数对
,则有序实数对![]() = .
= .
三、解答题(共6小题,共70分)解答应在答卷的相应各题中写出文字说明,证明过程或演算步骤.
17.(本题满分10分)
已知![]() ,其中
,其中![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)求函数![]() 的单调递增区间.
的单调递增区间.
18.(本题满分12分)
如图,在正方体![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 的中心.
的中心.
⑴ 证明![]() ⊥
⊥![]() ;
;
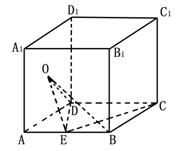 ⑵ 求二面角
⑵ 求二面角![]() 的大小(用反三角函数表示).
的大小(用反三角函数表示).
19.(本题满分12分)
设动点![]() 与两定点
与两定点![]() ,
,![]() 的距离之比为
的距离之比为![]() .
.
⑴ 求动点![]() 的轨迹
的轨迹![]() 的方程,并说明轨迹是什么;
的方程,并说明轨迹是什么;
⑵ 若轨迹![]() 与直线
与直线![]() 只有一个公共点,求
只有一个公共点,求![]() 的值.
的值.
20. (本题满分12分)
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且对任意正整数
,且对任意正整数![]() ,都有
,都有![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
⑴ 求证![]()
![]() ;
;
⑵ (文科)求数列![]() 的通项公式.
的通项公式.
(理科)求证 ![]() .
.
21.(本题满分12分)
有三个盒子,第一个盒里装有4个红球和1个黑球,第二个盒里装有3个红球2个黑球,第三个盒里装有2个红球3个黑球.如果先从这三个盒子中任取一个,再从中取出的盒子中任取3个球,以![]() 表示所取到的红球个数,求
表示所取到的红球个数,求
(文科)![]() 的概率及
的概率及![]() 的概率.
的概率.
(理科)![]() 的概率分布列及其数学期望.
的概率分布列及其数学期望.
22.(本题满分12分)
(文科)![]() ,
,![]() .
.
⑴ 当![]() 时,求
时,求![]() 的最小值;
的最小值;
⑵ 若![]() 在
在![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
(理科)已知函数![]()
![]() .
.
⑴ 当![]() 时,求
时,求![]() 的最小值;
的最小值;
⑵ 若![]() 在
在![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
文理科数学(答卷)
(文科:必修+选修Ⅰ;理科:必修+选修Ⅱ)
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 得 分 | |||||||||
第Ⅰ卷
| 得分 | 评卷人 | 一、选择题:(共12小题,每小题5分,共60分) |
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选 项 |
第Ⅱ卷
| 得分 | 评卷人 | 二、填空题(本大题共4小题,每小题5分,共20分)把答案填在题号后的横线上. |
13. 14. 15. 16.
三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.
| 得分 | 评卷人 | 17.(本题满分10分) |
| 得分 | 评卷人 | 18.(本题满分12分) |

| 得分 | 评卷人 | 19.(本题满分12分) |
| 得分 | 评卷人 | 20.(本题满分12分) |
| 得分 | 评卷人 | 21.(本题满分12分) |
| 得分 | 评卷人 | 22.(本题满分12分) |
文理科数学试题参考答案及评分标准
一、选择题(共12小题,每小题5分,共60分)
| 题 号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 选 项 | 文 |
|
|
|
|
|
|
|
|
| 文 |
|
1.(文科)选D.原不等式可化为![]() ,解得
,解得 ![]()
(理科)选A.![]()
![]()
2.选B.∵![]() ,
,![]() ∴
∴![]()
3.选B.∵![]() ∴
∴![]()
4.选C.∵双曲线![]() 的渐近线为
的渐近线为![]() ,准线为
,准线为![]() , 故夹角是
, 故夹角是![]()
5.选D.其中A、C既非充分也非必要条件,B充分非必要条件
6.选B.∵![]() =
=![]() ∴
∴![]()
7.选C.设![]() 与平面
与平面![]() 交于点
交于点![]() (
(![]() 是
是![]() 与
与![]() 的交点),
的交点),![]() ,易证
,易证![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,即
,即![]() ⊥平面
⊥平面![]() ,于是
,于是![]() 就是所求角.
就是所求角.
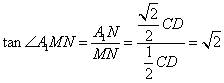
8.选A.设![]() ,它按
,它按![]() =
=![]() 平移后得到
平移后得到![]() ,由图知它过点
,由图知它过点![]() ,代入得
,代入得![]() ∴
∴![]() =
=![]()
9.选A.由![]() 得
得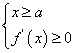 或
或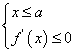 即
即![]() 时
时![]() 为增函数,
为增函数, ![]() 时
时![]() 为减函数,所以
为减函数,所以![]()
10.选D.∵![]() ∴直线
∴直线![]() 的方程为
的方程为![]() ,由
,由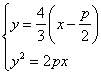 ,
,
得![]() ,
,![]() ;或
;或![]() ,
,![]()
∴由![]() ,得
,得![]() ,或
,或![]()
11.(文科)选A.设每一份为![]() 人,则共有
人,则共有![]() 人,由
人,由![]() ,得
,得![]() 所以,高三年级共有
所以,高三年级共有![]() 人
人
(理科)选A.令![]() ∵
∵![]() ~
~![]() ∴
∴![]() ~
~![]()
∴![]() =
=![]()
=![]() =
=![]()
∴体重属于正常情况的人数约是![]()
12.选C.不妨先染![]() 点,有
点,有![]() 种方法,再染
种方法,再染![]() 点,有
点,有![]() 种方法,若
种方法,若![]() 点与
点与![]() 点同色,则
点同色,则![]() 点有3种方法;若
点有3种方法;若![]() 点与
点与![]() 点不同色,则
点不同色,则![]() 点有
点有![]() 种染法,
种染法,![]() 点也有
点也有![]() 种染法.所 以共有
种染法.所 以共有![]()
![]()
![]() 种方法
种方法
二、填空题(共4小题,每小题5分,共20分)
13.![]() 14.
14.![]() 15.
15.![]() 16.
16.![]()
13.由已知可得![]() ,而
,而 ![]()
∴![]() ,
,![]()
14.![]()
15.∵![]() , 又∵
, 又∵![]() 时
时![]() ,
,
即![]() 时
时![]() ∴
∴![]()
16.∵![]()
![]()
![]()
![]()
∴![]() =
=![]()
三、解答题(共6小题,共70分)
17.![]() =
=![]() =
=![]()
∵![]() ∴
∴![]() ,
,
(1)由![]() 得
得![]()
∴![]() 或
或![]() ∴
∴![]() 或
或![]() …6分
…6分
(2)当![]() ,
, ![]() 时,
时, ![]() 随
随![]() 增大而增大,
增大而增大,
所以递增区间为 ![]() ,
, ![]() …10分
…10分
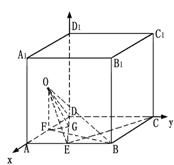 18.解法一:
18.解法一:
⑴过点![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,连接
,连接![]() ,
,
由已知及正方体的性质,易知![]() ⊥平面
⊥平面![]() ,
,
且![]() 是
是![]() 的中点,
的中点,![]() ⊥
⊥![]() ,
,
所以![]() ⊥
⊥![]() …4分
…4分
⑵过点![]() 作
作![]() ⊥
⊥![]() 于
于![]() ,连接
,连接![]() .
.
∵![]() ⊥平面
⊥平面![]() ,
,![]() ⊥
⊥![]() ,
,
![]() 平面
平面![]() .∴
.∴![]() ⊥
⊥![]() ,
,
于是![]() 就是二面角
就是二面角 ![]() 的平面角.
的平面角.
设![]() ,在
,在![]() 中,
中,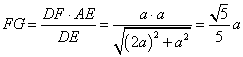
在![]() 中
中![]()
∴二面角![]() 的大小为
的大小为![]() …12分
…12分
解法二:如图建立直角坐标系,设正方体的棱长为![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .
.
⑴∵![]()
∴![]() ⊥
⊥![]() ,即
,即![]() ⊥
⊥![]() . …4分
. …4分
⑵易知平面![]() 的一个法向量是
的一个法向量是![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,于是
,于是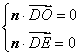
即![]() ,令
,令![]() ,∴
,∴![]()
∴![]()
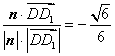
∴二面角![]() 的大小为
的大小为![]() (或
(或![]() ). …12分
). …12分
19.设点![]() ,由题意,得
,由题意,得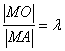 ,即
,即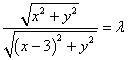 整理得
整理得
![]()
(1)当![]() 时,点
时,点![]() 的轨迹方程为
的轨迹方程为![]() ,表示的轨迹是线段
,表示的轨迹是线段![]() 的垂直平分线
的垂直平分线
当![]() 时,
时,![]() ,可化为
,可化为
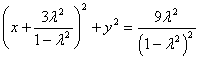
表示的是以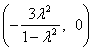 为圆心,
为圆心,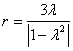 为半径的圆;
…6分
为半径的圆;
…6分
(2)当![]() 时,点
时,点![]() 的轨迹方程为
的轨迹方程为![]() 与直线
与直线![]() 只有一个公共点
只有一个公共点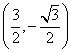 符合题意.
符合题意.
当![]() 时,圆
时,圆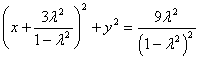 与直线
与直线![]() 只有一个公共点,所以圆心
只有一个公共点,所以圆心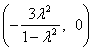 到直线
到直线![]() 的距离等于半径.
的距离等于半径.
即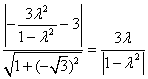 ,解之,得
,解之,得![]()
故当![]() 或
或![]() 时,轨迹
时,轨迹![]() 与直线
与直线![]() 只有一个公共点. …12分
只有一个公共点. …12分
20.(1)∵![]() 是
是![]() 与
与![]() 的等差中项,∴
的等差中项,∴![]() ,
,
于是![]()
![]()
两式相减得![]() 即
即![]()
∴![]()
![]() …4分
…4分
(2)(文科)当![]() 时,
时,![]() 即
即 ![]() ∴
∴![]()
∴ ![]() ∴
∴ ![]()
当![]() 时,由
时,由![]() 得
得 ![]() ∵
∵![]()
∴![]() 即
即![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列
为公比的等比数列
∴![]()
![]()
∴![]() …12分
…12分
(理科)当![]() 时,
时,![]() 即
即 ![]() ∴
∴![]() ,∴
,∴![]()
当![]() 时,∵
时,∵![]()
![]()
∴当![]() 时,
时,![]() =
=![]()
![]() =
=![]()
![]()
∴![]() …12分
…12分
21.设![]() 表示从三个盒子中取出第
表示从三个盒子中取出第![]() 个盒子时,
个盒子时,![]() 的概率,
的概率,![]() ;
;![]()
∵从三个盒子中任取一个盒子的概率为![]()
∴![]() =
=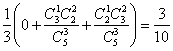
![]() =
=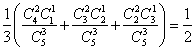
![]() =
=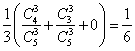
(文科)∴![]() ,
,![]() …12分
…12分
(理科)依题意知![]() ,
,
![]() =
=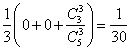
|
| 0 |
|
|
|
|
|
|
|
|
|
∴
![]() …12分
…12分
22.(1)![]() 时,
时,
(文科)![]()
当![]() 当
当![]() 故
故![]() …3分
…3分
(理科)![]()
当![]() 当
当![]() 故
故![]() …3分
…3分
(2)(文科)![]()
(理科)![]() 令
令![]()
∵![]() ∴文理科有以下相同的结论.
∴文理科有以下相同的结论.
(ⅰ)![]() 时,
时,![]() ,则
,则![]() ,于是
,于是![]() 符合要求;
符合要求;
(ⅱ)![]() 时,
时,![]() ,
,![]() ∴
∴![]() ,
,![]() ,即
,即![]()
于是![]() 符合要求;
符合要求;
(ⅲ)![]() 时,对
时,对![]() ,
,
要使![]() 是单调函数,则
是单调函数,则![]() 只可能是单调递减的.
只可能是单调递减的.
故△![]()
![]() ,或
,或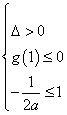
![]()
![]()
由(ⅰ),(ⅱ),(ⅲ)可知![]() .
…12分
.
…12分
以上各题的其它解法,限于篇幅从略,请相应评分.