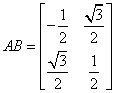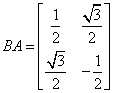08高考数学第二次调研考试模拟试卷
(考试时间：120分钟+30分钟 总分160分+40分)
必做题部分
一、填空题：（本大题共14小题，每小题5分，共70分．请将答案填入答题纸填空题的相应答题线上．）
1.设全集U={1, 3, 5, 7}，集合M=
，
，
={5, 7}，则实数a的值为_8___
2. 过点P(1，2)的直线l的与两点A(2，3)，B(4，－5)的距离相等，则直线l的方程为
3．已知
，
，若a和b的夹角为钝角，则
的取值范围是
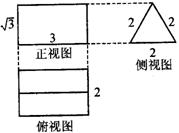
4．下图是一个几何体的三视图，已知侧视图是一个等边三角形，根据图中尺寸（单位: cm），可知这个几何体的表面积是
。
5．设两个平面
，
，直线l，下列条件：（1）l ⊥，（2）
，（3）
，若以其中两个为前提，另一个为结论，则构成三个命题，这三个命题中正确的命题个数为___1___
6．已知函数
在
上是减函数，则实数a的取值范围是（-8，-6]
7．已知定义域为{x x∈R，且x≠1}的函数
满足
，则
=__2______
8．已知关于x的方程
有实根，则纯虚数m的值是
9.在数列{an}中，对任意自然数n∈N*，a1+a2+…+an=2n－1，则
=
10．函数f : {1, 2, 3}→{1, 2, 3}，满足
，则这样的函数个数共有10
11.在一根长10cm，外圆周长6cm的圆柱体外表面，用一根细铁丝缠绕，组成10个螺旋，如果铁丝的两端恰好落在圆柱的同一条母线上，则铁丝长度的最小值为
.
12．与圆
相切，且在两坐标轴上截距相等的直线共有4条 。
13.如果
，且
，
则
=__2008___________
14.定义在R上的偶函数f (x)满足
，且在[－1，0]上是增函数，给出下面关于f (x)的判断：
① f (x)是周期函数；
② f (x)关于直线x=1对称；
③ f (x)在[0，1]上是增函数；
④ f (x)在[1，2]上是减函数；
⑤ f (2)= f (0)。
其中正确判断的序号为_①②⑤__（写出所有正确判断的序号）。
二、解答题：（本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤．）
15. 设锐角三角形ABC的内角A，B，C的对边分别为a，b，c，且a=2bsinA。
（1）求B的大小；
（2）求cosA+sinC的取值范围。
解：（1）
（2）cosA+sinC
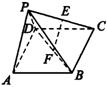
16．如图所示，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，侧面PAD⊥底面ABCD，且PA=PD=
AD，若E，F分别为PC，BD的中点，求证：
（1）EF//平面PAD；
（2）平面PDC⊥平面PAD。
解：略
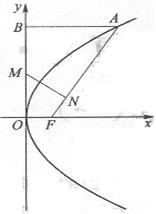17. 已知抛物线y2=2px（p>0）的焦点为F，A是抛物线上横坐标为4，且位于x轴上方的点，A到抛物线准线的距离等于5，过A作AB垂直于y轴，垂足为B，OB的中点为M（如图所示）。
（1）求抛物线方程；
（2）过M作MN⊥FA，垂足为N，求点N的坐标；
（3）以M为圆心，MB为半径作圆M。当K(m, 0)是x轴上一动点时，讨论直线AK与圆M的位置关系。
解：⑴抛物线y2=2px（p>0）的准线为
于是4+
=5，
抛物线方程是y2=4x.
⑵
⑶由题意得：圆心是（0，2）半径是2.
当
时直线AK的方程为x=4,此时直线AK与圆M相离
当
时直线AK的方程为
，
当
时直线AK与圆M相离；当
时直线AK与圆M相切;当
时直线AK与圆M相交。
18.已知数列{an}，当n为奇数时，
；当n为偶数时，
；且a1+a2=5。
（1）求数列{an}的通项公式；
（2）记Sn=a1+a2+…+an，求Sn。
解：（1）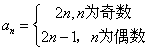
（2）当n为奇数时，Sn
，当n为偶数时Sn
19.定义在
的三个函数、
、
，已知
，
，
，且在
上为增函数，在
上为减函数。
（1）求，的表达式；
（2）求证：当x>1时，恒有
；
（3）把h(x)对应的曲线C1向上平移6个单位后得曲线C2，求C2与对应的曲线C3的交点个数，并说明理由。
解：（1）
，（可以得5分）
（2）略。（3）交点个数2个
20.已知函数f(x)的定义域为[0，1]，且同时满足：①f(1)＝3；②f(x)≥2对一切x∈[0，1]恒成立；③若x1≥0，x2≥0，x1＋x2≤1，则f(x1＋x2)≥f(x1)＋f(x2)－2，
（Ⅰ）求函数f(x)的最大值和最小值；
（Ⅱ）试比较
与
（n∈N）的大小；
（Ⅲ）某同学发现：当
（n∈N）时，有f(x)＜2x＋2，由此他提出猜想：对一切x∈(0，1]，都有f(x)＜2x＋2，请你判断此猜想是否正确，并说明理由．
（Ⅰ）设x1，x2∈[0，1]，x1＜x2，则x2－x1∈[0，1]．
∴f(x1)＝f[(x2－x1)＋x1]≥f(x2－x1)＋f(x1)－2．
∴f(x2)－f(x1)≥f(x2－x1)－2≥0．∴f(x1)≤f(x2)． ………………………… 2分
则当0≤x≤1时，f(0)≤f(x)≤f(1)． ………………………………………… 3分
在③中，令x1＝x2＝0，得f(0)≤2，由②得f(0)≥2，∴f(0)＝2． ……… 4分
∴当x＝0时，f(x)取得最小值为2；
当x＝1时，f(x)取得最大值为3． …………………………………………… 6分
（Ⅱ）在③中，令x1＝x2＝
，得
…………………… 8分
∴
则
． …………………………………………………………… 11分
（Ⅲ）对x∈[0，1]，总存在n∈N，满足
＜x≤． …………………… 13分
由（Ⅰ）与（Ⅱ），得
，又2x＋2＞2·＋2＝＋2．
∴f(x)＜x＋2．
综上所述，对任意x∈[0，1]．f(x)＜x＋2恒成立． ……………………… 16分
B．附加题部分
三、附加题部分（本大题共4小题,每题10分）
21.某气象站天气预报的准确率为80%，计算（结果保留到小数点后面第2位）：
（1）5次预报中恰有2次准确的概率；0.05
（2）5次预报中至少有2次准确的概率；0.99
（3）5次预报中恰有2次准确，且其中第3次预报准确的概率。0.02
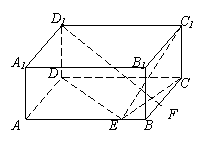
22. 如图,在长方体ABCD—A1B1C1D1中,
已知AB= 4, AD =3, AA1= 2. E、F分别是线段
AB、BC上的点，且EB= FB=1.
(I) 求二面角C—DE—C1的正切值;
(II) 求直线EC1与FD1所成的余弦值.
解: （I）以A为原点，
分别为x轴, y轴,z轴的正向建立空间直角坐标系,
则有D(0,3,0)、D1(0,3,2)、E(3,0,0)、F(4,1,0)、C1(4,3,2)
于是,
设向量
与平面C1DE垂直，则有
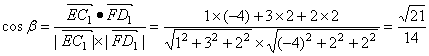
（II）设EC1与FD1所成角为β，则
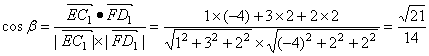
23.点P(x, y)在直线l：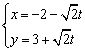
上运动，求直线l与抛物线y=2x2所围成的图形的面积
24．设TA是旋转角为300的旋转变换，TB是以直线l为轴的反射变换，Ox轴到直线l的角为450。求复合变换TATB、TBTA的矩阵。
解：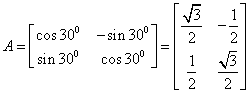
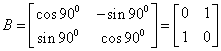
复合变换TATB、TBTA的矩阵分别是
