08高考数学方法讲解10综合法复习

08高考数学方法讲解10综合法复习

利用某些已经证明过的不等式和不等式的性质，推导出所要证明的不等式，这个证明方法叫综合法。

例1.已知a, bÎR⁺，求证：

【巧证】：∵a, bÎR⁺ ∴　　∴

∴

∴

∴

∴

例2.设a>0, b>0，且a + b = 1，求证：

【巧证】：∵　　 ∴　　∴

　　∴

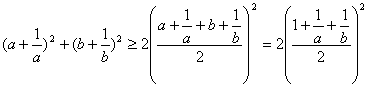
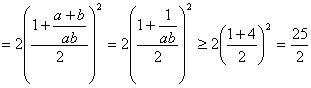
例3.已知a, b, c是不全相等的正数，

求证：a(b² + c²) + b(c² + a²) + c(a² + b²) > 6abc

　 【巧证】：∵b² + c² ≥ 2bc ,　a > 0 ,　∴a(b² + c²) ≥ 2abc

　　　　同理：b(c² + a²) ≥ 2abc ,　c(a² + b²) ≥ 2abc

　　　　∴a(b² + c²) + b(c² + a²) + c(a² + b²) ≥ 6abc

　　　　当且仅当b=c,c=a,a=b时取等号，而a, b, c是不全相等的正数

　　　　∴a(b² + c²) + b(c² + a²) + c(a² + b²) > 6abc

例4. a , b, cÎR,　求证：1°

2°

3°

【巧证】：1°法一：,　,　两式相乘即得。

　　　　 法二：左边

　　　　　　　　 　≥ 3 + 2 + 2 + 2 = 9

2°∵

　　

　 两式相乘即得

3°由上题：

∴

即：

巧练：设a, b, c Î R，

1°求证：

2°求证：

3°若a + b = 1,　求证：

　

十、综合法:

【巧证】：1°∵　　∴

　　　　 ∴

2°同理：，

三式相加：

3°由幂平均不等式：

∴
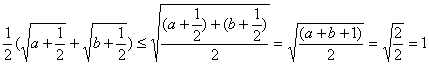