难点32 极限及其运算
极限的概念及其渗透的思想，在数学中占有重要的地位，它是人们研究许多问题的工具.旧教材中原有的数列极限一直是历年高考中重点考查的内容之一.本节内容主要是指导考生深入地理解极限的概念，并在此基础上能正确熟练地进行有关极限的运算问题.
●难点磁场
(★★★★)求
.
●案例探究
［例1］已知
(
－ax－b)=0,确定a与b的值.
命题意图：在数列与函数极限的运算法则中，都有应遵循的规则，也有可利用的规律，既有章可循，有法可依.因而本题重点考查考生的这种能力.也就是本知识的系统掌握能力.属★★★★★级题目.
知识依托：解决本题的闪光点是对式子进行有理化处理，这是求极限中带无理号的式子常用的一种方法.
错解分析：本题难点是式子的整理过程繁琐，稍不注意就有可能出错.
技巧与方法：有理化处理.
解：
要使上式极限存在，则1－a2=0,
当1－a2=0时，
∴
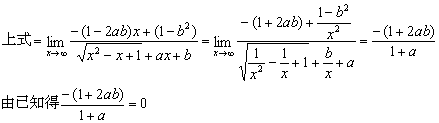
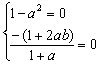解得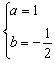
［例2］设数列a1,a2,…,an,…的前n项的和Sn和an的关系是Sn=1－ban－
,其中b是与n无关的常数，且b≠－1.
(1)求an和an－1的关系式；
(2)写出用n和b表示an的表达式；
(3)当0＜b＜1时，求极限
Sn.
命题意图：历年高考中多出现的题目是与数列的通项公式，前n项和Sn等有紧密的联系.有时题目是先依条件确定数列的通项公式再求极限，或先求出前n项和Sn再求极限，本题考查学生的综合能力.属★★★★★级题目.
知识依托：解答本题的闪光点是分析透题目中的条件间的相互关系.
错解分析：本题难点是第(2)中由(1)中的关系式猜想通项及n=1与n=2时的式子不统一性.
技巧与方法：抓住第一步的递推关系式，去寻找规律.
解：(1)an=Sn－Sn－1=－b(an－an－1)－
=－b(an－an－1)+
(n≥2)
解得an=
(n≥2)
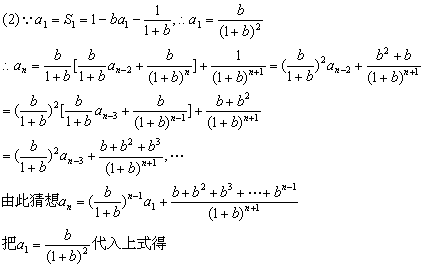
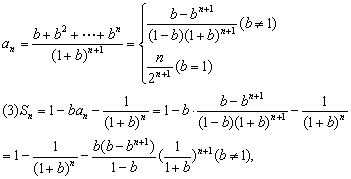
●锦囊妙计
1.学好数列的极限的关键是真正从数列的项的变化趋势理解数列极限.
学好函数的极限的关键是真正从函数值或图象上点的变化趋势理解函数极限.
2.运算法则中各个极限都应存在.都可推广到任意有限个极限的情况，不能推广到无限个.在商的运算法则中，要注意对式子的恒等变形，有些题目分母不能直接求极限.
3.注意在平时学习中积累一些方法和技巧，如：
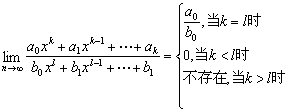
●歼灭难点训练
一、选择题
1.(★★★★)an是(1+x)n展开式中含x2的项的系数，则
等于( )
A.2 B.0 C.1 D.－1
2.(★★★★)若三数a,1,c成等差数列且a2,1,c2又成等比数列，则
的值是( )
A.0 B.1 C.0或1 D.不存在
二、填空题
3.(★★★★) 
=_________.
4.(★★★★)若
=1,则ab的值是_________.
三、解答题
5.(★★★★★)在数列{an}中，已知a1=
,a2=
,且数列{an+1－
an}是公比为
的等比数列，数列{lg(an+1－an}是公差为－1的等差数列.
(1)求数列{an}的通项公式；
(2)Sn=a1+a2+…+an(n≥1),求Sn.
6.(★★★★)设f(x)是x的三次多项式，已知
=1,试求
的值.(a为非零常数).
7.(★★★★)已知数列{an},{bn}都是由正数组成的等比数列，公式分别为p、q,其中p＞q,且p≠1,q≠1,设cn=an+bn,Sn为数列{cn}的前n项和，求
的值.
8.(★★★★★)已知数列{an}是公差为d的等差数列，d≠0且a1=0,bn=2
(n∈N*),Sn是{bn}的前n项和，Tn=
(n∈N*).
(1)求{Tn}的通项公式；
(2)当d＞0时，求Tn.
参考答案
难点磁场
歼灭难点训练
一、1.解析：
，
答案：A
2.解析：
答案：C
二、3.解析：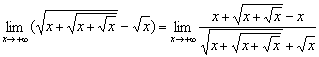
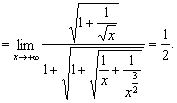
答案：
4.解析：原式=
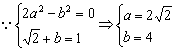
∴a·b=8
答案：8
三、5.解：(1)由{an+1－an}是公比为的等比数列，且a1=,a2=,
∴an+1－an=(a2－a1)()n-1=(－×)()n-1=
,
∴an+1=an+
①
又由数列{lg(an+1－an)}是公差为－1的等差数列，且首项lg(a2－a1)
=lg(－×)=－2,
∴其通项lg(an+1－an)=－2+(n－1)(－1)=－(n+1),
∴an+1－an=10－(n+1),即an+1=an+10－(n+1) ②
①②联立解得an=
［()n+1－()n+1］
(2)Sn=
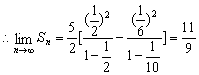
6.解：由于
=1，可知，f(2a)=0 ①
同理f(4a)=0 ②
由①②可知f(x)必含有(x－2a)与(x－4a)的因式，由于f(x)是x的三次多项式，故可设f(x)=A(x－2a)(x－4a)(x－C),这里A、C均为待定的常数，
,即4a2A－2aCA=－1 ③
同理，由于
=1,得A(4a－2a)(4a－C)=1,即8a2A－2aCA=1 ④
由③④得C=3a,A=
,因而f(x)= (x－2a)(x－4a)(x－3a),
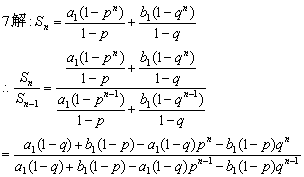
由数列{an}、{bn}都是由正数组成的等比数列，知p＞0,q＞0
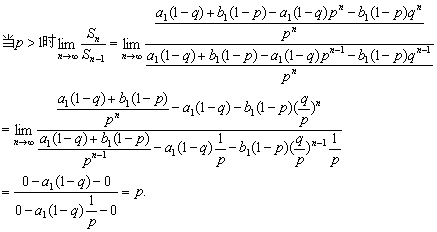
当p＜1时,q＜1, 
8.解：(1)an=(n－1)d,bn=2=2(n－1)d
Sn=b1+b2+b3+…+bn=20+2d+22d+…+2(n－1)d
由d≠0,2d≠1,∴Sn=
∴Tn=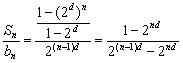
(2)当d＞0时，2d＞1
