08高考数学模拟测试试题
一、选择题（本大题共8小题，每小题5分，满分40分．在每小题给出的四个选项中，只有一项是符合题目要求的）
1、计算复数(1－i)2－
等于（ ）
A.0 B.2 C. 4i D. －4i
2、设集合A={－1, 0, 1}，集合B={0, 1, 2, 3}，定义A＊B={(x, y) x∈A∩B, y∈A∪B}，则A＊B中元素个数是（ ）
A.7 B.10 C.25 D.52
3、若函数y=log2ax－1的图象的对称轴为x=2，则非零实数a的值是（ ）
A.－2 B.2 C.
D. －
4、已知函数
则
的值为（ ）
A．10 B．-10 C．-20 D．20
5、等差数列{an}的前n项和为Sn，若S17为一确定常数，则下列各式也为确定常数的是（ ）
A．a2 + a15 B． a2·a15 C．a2 + a9 +a16 D． a2·a9·a16
6、下列四个命题
①线性相差系数r越大，两个变量的线性相关性越强；反之，线性相关性越小；
②残差平方和越小的模型，拟合的效果越好；
③用相关指数R2来刻画回归效果，R2越小，说明模型的拟合效果越好。
④随机误差e是衡量预报精确度的一个量，它满足E（e）=0
A．①③ B．②④ C．①④ D．②③
7、O为△ABC的内切圆圆心，且AB=5、BC=4、CA=3，
下列结论中正确的是（ ）
A．
B. 
>
C. 
=
=
D. 
<=
8、某中学生为了能观看2008年奥运会，从2001年起，每年2月1日到银行将自己积攒的零用钱存入
元定期储蓄，若年利率为
且保持不变，并约定每年到期存款均自动转为新的一年定期，到2008年将所有的存款及利息全部取回，则可取回钱的总数（元）为
（ ）
A．
B．
C．
D．
二、填空题：本大题共7小题，其中13～15题是选做题，考生只能选做两题，三题全答的，只计算前两题得分．每小题5分，满分30分．
9、
---------------------------。
|
在
单调递增，且对任意实数
恒有
，若
，则的取值范围是------------------------------。
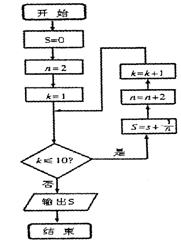
11、已知程序框图如右图所示，则该程
序框图的功能是----------------------------------------------------。
| 4 | ||||||||
| 9 | A | 3 | 5 | 7 | ||||
| 2 | 6 | 3 | 5 | |||||
| 4 | 2 | 8 | 6 | 9 | ||||
| 1 | 7 | |||||||
| 6 | 9 | 3 | 5 | 4 | ||||
| 2 | 8 | 9 | B | 5 | ||||
| 1 | 2 | 8 | 7 | 6 | ||||
| 4 |
12、近几年来，在欧美等国家流行一种“数独”推理游戏，游戏规则如下：
①在9×9的九宫格子中,分成9个3×3的小九宫格,用1到9这9个数字
填满整个格子; ②每一行与每一列都有1到9的数字，每个小九宫格里 也有1到9的数字，并且一个数字在每行、每列及每个小九宫格里只能出现一次，既不能重复也不能少. 那么A处应填入的数字为-----------；B处应填入的数字为------------.
13、极坐标方程
所表示的曲线的直角坐标方程是 ------------------------------------------
。
14、已知
都是正数，且
则
的最小值是
-------------------------。
15．已知圆
的半径为
，从圆外一点
引切线
和割线
，
圆心到
的距离为
，
，则切线的长为 -----------------------。
三、解答题：本大题共6小题，共80分. 解答应写出文字说明、证明过程或演算步骤.
16、计算机考试分理论考试与上机操作考试两部分进行，每部分考试成绩只记“合格”与“不合格”，两部分考试都“合格”则计算机考试“合格”并颁发“合格证书”。甲、乙、丙三人在理论考试中合格的概率分别为
，
，
；在上机操作考试中合格的概率分别为
，
，
。所有考试是否合格相互之间没有影响。
（1）甲、乙、丙三人在同一次计算机考试中谁获得“合格证书”可能性最大？
（2）用
表示甲、乙、丙三人在理论考核中合格人数，求的分布列和数学期望
。
17、在△ABC中角A、B、C的对边分别为
设向量
（1）求
的取值范围 （2）若
试确定实数的取值范围.
18
|
（其中M、N分别是AF、BC的中点）
（I）求证：MN∥平面CDEF；
（II）求二面角D—MN—B的余弦值的绝对值
19、已知曲线
；
（1）由曲线
上任一点
向
轴作垂线，垂足为
，点
分
所成的比为
。问：点的轨迹可能是圆吗？请说明理由；
（2）如果直线
的斜率为
，且过点
，直线交曲线于
，
两点，又
，求曲线的方程。
20、（本小题满分14分）已知点列
在直线l：y = 2x + 1上，P1为直线l与 y轴的交点，等差数列{an}的公差为
（Ⅰ）求{an}、{bn}的通项公式；
（Ⅱ）若数列
满足：
数列的前n项之和；
（Ⅲ）若
，且d1
= 1，求{dn}的通项公式
20、对于三次函数
。
定义：（1）设
是函数
的导数
的导数，若方程
有实数解
，则称点
为函数的“拐点”；
定义：（2）设为常数，若定义在
上的函数对于定义域内的一切实数，都有
成立，则函数的图象关于点对称。
己知
，请回答下列问题：
（1）求函数的“拐点”的坐标
（2）检验函数的图象是否关于“拐点”对称，对于任意的三次函数写出一个有关“拐点”的结论（不必证明）
（3）写出一个三次函数
，使得它的“拐点”是
（不要过程）
B B C C C B A D
4
求数列
的前10项和
1，3
13、
；
14、12； 15．
16、（Ⅰ）记“甲计算机考试获得合格证书”为事件A，记“乙计算机考试获得合格证书”为事件B，记“丙计算机考试获得合格证书”为事件C，则
，
，
，有
，故丙获得“合格证书”可能性最大； ……3分
（Ⅲ）（理科）用表示甲、乙、丙三人在理论考核中合格人数，则可以取0，1，2，3，故的分布列如下：
|
| 0 | 1 | 2 | 3 |
| P（ |
|
|
|
|
……10分
的数学期望：
=0×
+1×
+2×
+3×
=
…………………12分
17、解：因为
所以
，-------------------------------------------1分
由正弦定理，得
，
即
-------------------------------------------------2分
又
所以
即
.--------------------------------------------------------3分
(1)=
------4分
因此的取值范围是
-----------------------------6分
(2)若则
,
由正弦定理，得
--------------8分
设
=
,则
,
所以
-------------------------------------------10分
即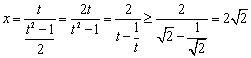
所以实数的取值范围为
.----------------------------------12分
18、18、（本小题满分12分）
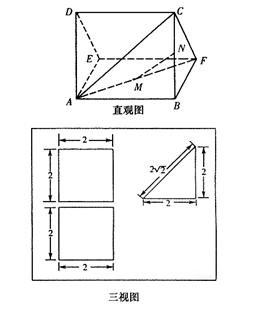
解：由三视图可知，该多面体是底面为直
角三角形的直三棱住ADE—BCF，……2分
且AB=BC=BF=2，DE=CF=2
∴∠CBF=
…………………………3分
（I）取BF中点G，连MG、NG，由M、N分别为AF、BC
的中点可得，NG∥CF，MG∥EF，
∴平面MNG∥平面CDEF，
∴MN∥平面CDEF ………………………………6分
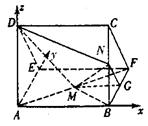
（II）建立空间直角坐标系，如图，
则A（0，0，0），B（2，0，0），D（0，0，2），F（2，2，0）
M（1，1，0），C（2，0，2），N（2，0，1），
|
，
……………………8分
设平面DMN的法向量
则
，
则
；……………………………………………………………………9分
设平面MNB的法向量为
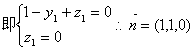…………………………………………………10分
设二面角D—MN—B的平面角为
，则
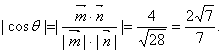
∴二面角D—MN—B的余弦的绝对值为
……………………………………12分
19、（1）
，
。
。
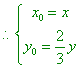……… 3分
。
……… 6分
（2）、
， 
。
，
。
。
………10分
、、
，
。
。
。
，
。
。
。
………14 分
19、解：∵在直线l:y=2x+1，
∴bn=2an+1……………………0分
∵P1为直线l与y轴交点，
∴P1=（0，1）
∴a1=0……………………2分
又数列
的公差为1
∴an=n－1（n∈N*）……………………4分
∴
（Ⅱ）∵P1=（0，1），Pn（an,bn）
∴
…………………5分
∵
……………………7分
∴
………8分
∴
……………………9分
（Ⅲ）∵
∴
……………………12分
∴
是以2为公比，4为首项的等比数列
∴
∴
……………………13分
20、（1）依题意，得：
，
。……………………2分
由 ，即
。∴
，又 
，
∴的“拐点”坐标是
。……………………4分
（2）由(1)知“拐点”坐标是。
而
=
=
=
，
由定义(2)知：
关于点对称。……………………8分
一般地，三次函数
的“拐点”是
，它就是的对称中心。………………………………………………………………………10分
（或者：任何一个三次函数都有拐点；任何一个三次函数都有对称中心；任何一个三次函数平移后可以是奇函数………）都可以给分
（3）
或写出一个具体的函数,如
或
。…………12分
说明：本题在函数、导数、方程的交汇处命题，具有较强的预测性，而且设问的方式具有较大的开放性，情景新颖.解题的关键是：深刻理解函数“拐点”的定义和函数图像的对称中心的意义。其本质是：任何一个三次函数都有拐点；任何一个三次函数都有对称中心；且任何一个三次函数的拐点就是它的对称中心，即。
一、选择题：本大题共10小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的．
1．已知全集
等于（ ）
A．{1，4} B．{2，6} C．{3，5} D．{2，3，5，6}
2．已知
的值为 （ ）
A．
B．
C．
D．
3．已知Sn是等比数列
等于
（ ）
A．
B．－ C．
D．－
4．已知x、y满足约束条件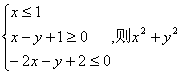
的最小值为
（ ）
A．
B．
C．1 D．
5．已知条件p：:x≤1，条件，q：
<1，则
p是q的 （ ）
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．即非充分也非必要条件
6．甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性作试验，并用回归分析方法分别求得相关系数r与残差平方和m如下表： （ ）
| 甲 | 乙 | 丙 | 丁 | |
| r | 0.82 | 0.78 | 0.69 | 0.85 |
| m | 106 | 115 | 124 | 103 |
则哪位同学的试验结果体现A、B两变量有更强的线性相关性？
A．甲 B．乙 C．丙 D．丁
7．现有甲、已、丙三个盒子，其中每个盒子中都装有标号分别为1、2、3、4、5、6的六张卡片，现从甲、已、丙三个盒子中依次各取一张卡片使得卡片上的标号恰好成等差数列的取法数为（ ）
Ａ．14 Ｂ．16 Ｃ．18 Ｄ．20
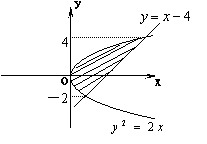
8.右图中,阴影部分的面积是 ( )
A.16 B.18 C.20 D.22
第二部分 非选择题(共100分)
二、填空题：本大题共7小题，其中（9）～（12）是必做题，（13）～（15）是选做题，要求考生只从（13）、（14）、（15）题中任选2题作答，三题都作答的只计算前两题的得分。每小题5分，满分30分.
9复数
的虚部是
。
10．已知
中，
，则
=__________。
11．.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如下图所示，则这个棱柱的体积为 。
12．在算式“9×△+1×□=48”中的△，□中，分别填入两个正整数，使它们的倒数和最小，则这两个数构成的数为（△，□）应为 。
三、解答题：本大题共6小题，共80分．解答应写出文字说明、演算步骤或推证过程．
16．（本小题满分12分）
设函数
，其中向量
（1）
若函数
（2）
若函数
的图象按向量
平移后得到函数的图象，求实数m及n的值。
17．（本小题满分12分）
甲、乙两射击运动员进行射击比赛，射击次数相同，已知两运动员射击的环数稳定在7，8，9，10环，他们的这次成绩的频率分布直方图如下：
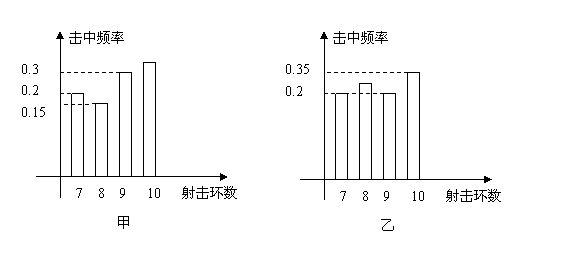
（1） 求乙运动员击中8环的概率，并求甲、乙同时击中9环以上（包括9环）的概率。
（2）
求甲运动员射击环数的概率分布列及期望；若从甲、乙运动员中只能挑选一名参加某大型比赛，你认为让谁参加比较合适？
18．（本小题满分14分）
|
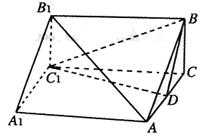
（Ⅰ）求证：AB1//面BDC1；
（Ⅱ）求二面角C1—BD—C的余弦值；
（Ⅲ）在侧棱AA1上是否存在点P，使得
CP⊥面BDC1？并证明你的结论.
19．（本小题满分14分）
已知双曲线的中心在原点，焦点F1、F2在坐标轴上，离心率为
且过点(4，-
)
（1）求双曲线方程；
（2）若点M(3,m)在双曲线上，求证：点M在以F1F2为直径的圆上；
（3）求△F1MF2的面积.
20．（14分）设关于的方程
的两根分别为
、
，函数
（1）证明在区间
上是增函数；
（2）当
为何值时，在区间
上的最大值与最小值之差最小
21．（本小题满分14分）已知函数
且任意的、
都有
（1）若数列
（2）求
的值.