08高考数学模拟试卷（一）
班级 姓名 成绩
一．填空题：本大题共有14小题，每小题5分，共70分，把答案填在题中横线上．
(1)
已知向量
，
，若
，则
=____________．
(2)
命题“
”的否命题是____________________________________．
(3)
若规定
的解集是____________．
(4)
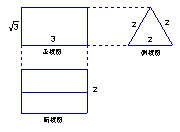
下图是一个空间几何体的三视图,根据图中尺寸(单位:
),可知几何体表面积是____________．
(5)
经过点
且在两坐标轴上的截距相等的直线方程是______________________．
(6)
双曲线的两条渐近线的夹角为
，则双曲线的离心率是___________________．
(7)
若
的图象关于
对称，则实数的值是__________．
(8)
若
是纯虚数，则
的值为____________．
(9)
已知
,若
是第二象限角，则实数的值是____________．
(10)
在
中，
，则
等于__________．
(11) 设非零向量,,,若= + + ,则的取值范围是___________．
(12)
设命题p：函数
的定义域为R，命题q：函数
的值域为R，若命题p、q有且仅有一个正确，则c的取值范围为___________．
(13) 已知在平面直角坐标系中,
,动点
满足不等式
则
的最大值为__________．
(14) 已知
是定义在R上的偶函数，定义在R上的奇函数
过点
且
，则
=___________．
三．解答题：本大题共6小题，共90分．解答应写出文字说明，证明过程或演算步骤．
(15) (本小题满分14分)
已知向量 = (cos x,sin x)， = (－cos x,cos x)， = (－1,0)
(Ⅰ)若 x = ，求向量 、 的夹角；
(Ⅱ)当 x∈[,] 时，求函数 f (x) = 2· + 1 的最大值。
(16) (本小题满分14分)
已知函数
.
(Ⅰ) 求求函数的单调区间； (Ⅱ) 求函数的极值
(17) (本小题满分16分)
用水清洗一堆蔬菜上残留的农药的效果假定如下：用x单位量的水清洗一次以后，蔬菜上残留的农药量与这次清洗前残留的农药量之比为
．
（Ⅰ）试解释
的实际意义；
（Ⅱ）现有a（a＞0）单位量的水，可以清洗一次，也可以把水平均分成2份后清洗两次．哪种方案清洗后蔬菜上残留的农药比较少？请说明理由．
(18) (本小题满分16分)
已知Ｏ为坐标原点，A（0,2），B（4,6），
.
(Ⅰ) 求点M在第二或第三象限的充要条件；
(Ⅱ) 求证：当
；
(Ⅲ) 若
(19) (本小题满分16分)
已知函数
将
的图象向右平移两个单位，得到
的图象．
(Ⅰ) 求函数的解析式；
(Ⅱ) 若函数
与函数的图象关于直线
对称，求函数的解析式；
(Ⅲ) 设
已知的最小值是
，且
求实数
的取值范围．
(20) (本小题满分16分)
设函数
(Ⅰ) 求证：为奇函数的充要条件是
；
(Ⅱ) 设常数
，且对任意
恒成立，求实数a的取值范围。
参考答案
一．填空题：
1.=3； 2. “
”． 3.
． 4.
．
5.
． 6.
． 7.-1． 8.-1． 9.
．
10.
． 11. [0，3]．
12. [-1，1]． 13.3． 14.-1．
三．解答题：
15.解：(I) 当 x = 时，cos <a,c> = =
= －cos x = －cos = cos ∵ 0≤<a,c>≤p， ∴ <a,c> =
(II) f (x) = 2a·b + 1 = 2 (－cos 2 x + sin x cos x) + 1 = 2 sin x cos x－(2cos 2 x－1)
= sin 2x－cos 2x = sin (2x－)∵ x∈[,]，∴ 2x－∈[,2p]，
故 sin (2x－)∈[－1,] ∴ 当 2x－= ，即 x = 时，f (x)max = 1
16.解:（1）由 得 
当
当
∴函数
（2）令
由（1）知，函数
内单调递增，在(－1,3)内单调递减，
∴当
∵函数
当
17.解：（I）f（0）=1．表示没有用水清洗时，蔬菜上的农药量没有变化．
（Ⅱ）设清洗前蔬菜上的农药量为1，那么用a单位量的水清洗1次后．残留的农药量为 W1=1×f（a）=
； 又如果用
单位量的水清洗1次，残留的农药量为1×f（）=
，
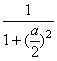此后再用单位量的水清洗1次后，残留的农药量为
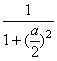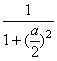W2=·f（）=[]2=
．
由于W1－W2=－=
，
故当a>2
时，W1>W2，此时，把a单位量的水平均分成2份后，清洗两次，残留的农药量较少；当a=2时，W1=W2，此时，两种清洗方式效果相同；当a<2时，W1<W2，此时，把a单位量的水清洗一次，残留的农药量较少．
18.解：
＝
＝
当点M在第二或第三象限时，有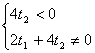
故所求的充要条件为 
﹤０ 
证明：当
∵ 
∴ A、B、M三点都共线
（3）解：当
又
∴
故
又
点M到直线AB：
∵
∴
解得 
故所求
19.解：(1)由题设，
．
(2)设
的图象上，
的图象上，则
，
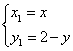即
．
(3)由题设，
＝
①当
时，有
，
，而
，
，
，这与
的最小值矛盾；
②当
时，有，
， 在
上是增函数，故不存在最小值；
③当
时，有
，
，此时在上是减函数，故不存在最小值；
④当
时，有，，
．
当且仅当
时取得等号，取最小值
又
及，得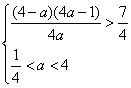
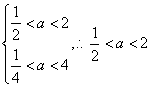
20.解：（I）充分性：若
，对一切x∈R恒成立，
是奇函数
必要性：若是奇函数，则对一切x∈R，
恒成立，即
令
再令
（II）
取任意实数不等式恒成立，
故考虑
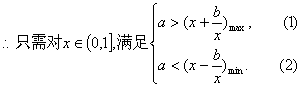
对（1）式，由b < 0时，在
为增函数，
（3）
对（2）式，当
当
（4）
由（3）、（4），要使a存在，必须有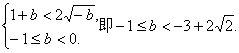
∴当
当
为减函数，（证明略）
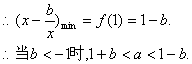
综上所述，当
的取值范围是
；
当
的取值范围是
解法二：
由于b是负数，故
（1）
，
则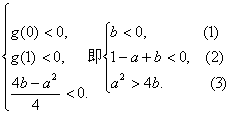
其中（1），（3）显然成立，由（2），得
（*）
（2）
，
①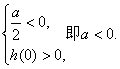
综合（*），得
值不存在
②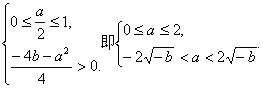
综合（*），得
③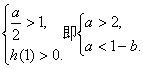
综合（*），得
不存在
综上，得