新高考高三数学复习的几点思考(江苏省教育学会高考信息研究会)
2008年3月15日
一.首先,必须让学生知道新高考考什么?
新高考来了,尽管大家对新高考有这样那样的看法,但是我们还是必须面对它,研究它.为了让学生知道新高考考什么,对于教师来说,必须研究新高考的指导思想是什么?研究课程改革的理念, 研究新高考与课程改革的关系,研究新高考与原高考的区别等等,从而明确新高考考什么.
高考的方式,高考的内容可以变, 但是用数学的思想,数学的方法去培养学生的能力这一数学教育目的没有变, 因此,在数学高考的复习中, 用数学的思想,数学的方法去提高学生的数学思维能力还是数学复习的基本方法,基本指导思想.
二.让学生的解题思维有数学思想的指导
解题必须有思想的指导,也就是说,数学解题的基本方法是具有思想性的. 数学的思想是数学基本方法的灵魂.
在数学复习中,有意识地揭示这些数学基本方法中所隐含的数学思想, 在数学学习活动中形成一些数学的观点;在数学知识结构的形成、完善过程中,有意识地用数学的观点去观察、分析数学问题,不断地获取、积累、深化这些数学的观点,使这些数学的观点能够在数学思维中升华为数学意识,从而就能从根本上提高思维能力, 提升思维层次,提高数学能力,这是数学学习的有效方法之一,也是数学学习的目的.
例1.已知 ![]() ,
, ![]() ,求
,求 ![]() 的值.
的值.
分析(1) ![]() ,
,![]() ,
,![]() 在公式
在公式![]()
![]()
![]() 中是联系在一起的,由此,我们可以下面的解法.
中是联系在一起的,由此,我们可以下面的解法.
解法(1) ∵ ![]()
![]()
![]() ,
,
∴ ![]() =
=![]()
![]() =
=![]() =8.
=8.
分析(2) 显然由![]() 和
和![]() 要分别解出
要分别解出![]() 的值是不可能的,但是,我们可以利用
的值是不可能的,但是,我们可以利用![]() 和
和![]() 消去
消去![]() 中的变元,从而得
中的变元,从而得![]() 的值,也就是说,消元就是解这个问题的指导思想,而且, 消元在代数式的求值中具有一般的指导意义.
的值,也就是说,消元就是解这个问题的指导思想,而且, 消元在代数式的求值中具有一般的指导意义.
解法(2) ∵ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]() =
=![]()
=![]()
=![]()
=8.
例2. 设![]() ,求证:
,求证:![]() .
.
证明方法(一):
![]() =
=![]()
![]()
=![]() (1)
(1)
>![]()
故![]() 成立.
成立.
证明方法(二)
![]() =
=![]()
![]() =
=![]()
∴
![]()
![]() =
=![]() =
=![]()
![]()
故![]() 成立.
成立.
问题: ①表达式(1)是如何冒出来的? ②证明方法(一)与证明方法(二)有什么关系?
例3.化简:![]() .
.
分析: 这是一个极容易的化简题, 学生很可能盲目地获得结果.我们要问: 解本题的指导思
想是什么?
先看下面两个解法:
解法(一): 原式=![]()
=![]()
=![]()
=![]()
=1
解法(二): 原式=![]()
=![]()
=1
说明: 证明方法(一)中将被化简式的表达形式与公式挂钩不容易, 因此,这一种方法的
技巧性较强.证明方法(二)的指导思想是:“消元”. 我们又要问:消元的方法是什么? 回答是: ① 减少三角函数名称,② 减少角的表达形式.
由证明方法(二)的指导思想还可以获得以下证明方法:
解法(三) 原式消元成只含![]() 的表达式而被化简.
的表达式而被化简.
原式=![]()
=![]()
=1
解法(四) 原式消元成只含![]() 的表达式而被化简.
的表达式而被化简.
原式=![]()
=![]()
![]()
=1
例4.已知圆![]() ,直线
,直线![]() 过定点A (1,0).
过定点A (1,0).
(1)若![]() 与圆相切,求
与圆相切,求![]() 的方程;
的方程;
(2)若![]() 与圆相交于P,Q两点,线段PQ的中点为M,又
与圆相交于P,Q两点,线段PQ的中点为M,又![]() 与
与![]() 的交点为N,判断
的交点为N,判断![]() 是否为定值,若是,则求出定值;若不是,请说明理由.
是否为定值,若是,则求出定值;若不是,请说明理由.
(1) 解:①若直线![]() 的斜率不存在,即直线是
的斜率不存在,即直线是![]() ,符合题意.
,符合题意.
②若直线![]() 斜率存在,设直线
斜率存在,设直线![]() 为
为![]() ,即
,即![]() .
.
由题意知,圆心(3,4)到已知直线![]() 的距离等于半径2,即:
的距离等于半径2,即: ![]() ,
,
解之得 ![]() .
.
所求直线方程是![]() ,
,![]() 。
。
(2) 解法一:直线与圆相交,斜率必定存在,且不为0,可设直线方程为![]()
由![]() 得
得![]() .
.
又直线CM与![]() 垂直,由
垂直,由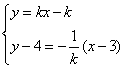 得
得![]() .
.
∴ ![]()
![]() 为定值.
为定值.
故![]() 是定值,且为6.
是定值,且为6.
解法二:直线与圆相交,斜率必定存在,且不为0,可设直线方程为![]() .
.
由![]() 得
得![]() .
.
再由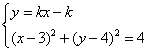 得
得![]() .
.
 ∴
∴ ![]() 得
得![]() .
.
以下同解法一.
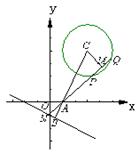
解法三:用几何法,
如图所示,△AMC∽△ABN,则![]() ,可得
,可得![]() ,是定值.
,是定值.
说明: 显然, 由于应用了平面几何知识, 解法(三)比解法(一)、解法(二)简洁.
例5. 双曲线![]() 的离心率为
的离心率为![]() ,A、F分别是双曲线的左顶点、右焦点,过点F的直线
,A、F分别是双曲线的左顶点、右焦点,过点F的直线![]() 交双曲线的右支于P、Q两点,交y轴于R点,AP、AQ分别交右准线于M、N两点.
交双曲线的右支于P、Q两点,交y轴于R点,AP、AQ分别交右准线于M、N两点.
(1) 若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2) 证明:M、N两点的纵坐标之积为![]() .
.
解: (1)解:设![]() ,
,
∵ 双曲线的离心率为![]() , ∴
, ∴ ![]() ,双曲线方程为
,双曲线方程为![]() ,
,
∵ ![]() , ∴
, ∴![]() ,
,
∵ 直线![]() 为
为![]() , ∴
, ∴ ![]() ,
,
∵ 点Q是双曲线上一点, ∴ ![]() ,整理得,
,整理得,![]()
解得![]() .
.
(2)证明:设![]() 由题设可知:直线
由题设可知:直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
∴ 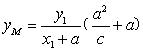 ,
,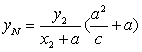
∴ ![]() ,
,
由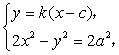 得
得![]()
∴ ![]() ,
,
![]() ,
,
![]()
∴ ![]() .(k不存在要作特殊处理)
.(k不存在要作特殊处理)
例6. (扬州市2008届高三第二次调研测试)
已知圆C:![]() ,直线
,直线![]() ,且直线
,且直线![]() 与圆C交于
与圆C交于![]() ,点
,点![]() 满足
满足![]() .
.
(1) 当![]() 时,求
时,求![]() 的值;
的值;
(2) 若![]() ,求
,求![]() 的取值范围.
的取值范围.
解:(1)当![]() 时,点
时,点![]() 在圆上,故当且仅当直线
在圆上,故当且仅当直线![]() 过圆心
过圆心![]() 时满足
时满足![]() ,
,
∵ 圆心![]() 的坐标为(1,1), ∴
的坐标为(1,1), ∴ ![]() .
.
设![]() ,
,
由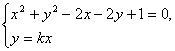 消去
消去![]() 可得,
可得,![]() ,
,
![]() ,
, ![]() ,
,
∵ ![]() , ∴
, ∴ ![]() ,
,
∴ ![]() ,
, ![]() ,
,
即 ![]() ,
,
∴ ![]() ,
,
![]()
方法(1) 对![]() 进行整理
进行整理![]() ,
,
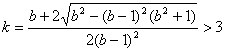
方法(2) 对![]() 进行整理
进行整理![]() ,
,
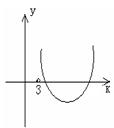
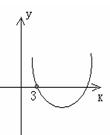
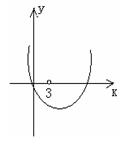
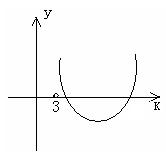
令![]()
![]() , 则函数
, 则函数![]() 的图象与
的图象与![]() 轴在
轴在![]() 上有公共点,若
上有公共点,若![]() ,则
,则![]() ,故
,故![]() 不可取.
不可取.
 故
故
∴ ![]() 或
或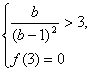
![]() 或
或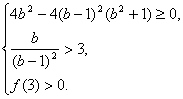
![]() 或
或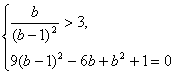 或
或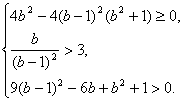
显然, 方法(1)和(2)不易求解.
方法(3) 由![]() 得,
得,![]()
![]()
① 令 ![]()
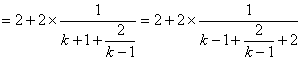 (
(![]() )
)
∴ ![]() ,
, ![]() ,
, 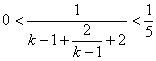 ,
,
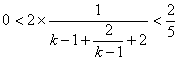 ,
, 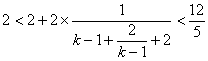
∴ 2<![]() , 解得,
, 解得,![]() 或
或![]()
② 令 ![]() ,则
,则![]()
∴ ![]() 在
在![]() 上为单调减函数,
上为单调减函数,
∴ ![]()
∵ ![]() =
=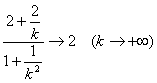
∴ 2![]() , 2
, 2![]()
![]() , 解得,
, 解得,![]() 或
或![]()
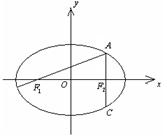
例7.苏、锡、常、镇四市2007年第二次模拟考试题(题20)
已知点![]() 都在椭圆
都在椭圆![]() (
(![]() )上,
)上,![]() 分别过两个焦点
分别过两个焦点![]() ,当
,当![]() 时,有
时,有![]() 成立.
成立.
(1)求此椭圆的离心率;
(2)设![]() ,
,![]() ,当点A在椭圆上运动时,
,当点A在椭圆上运动时,
求证: ![]() 始终是定植.
始终是定植.
分析: 本题是一个求值的问题. 在高中数学中, 求值的一般方法是:一是给出未知量的方程,解这个方程得值,题(1)可用这一思想;二是给出未知量的函数表达式,对表达式消元得值,题(2)可用这一思想.题(2)给出未知量的函数表达式的方法有两种:
 (1)
解: 当
(1)
解: 当![]() 时,
时,![]() ,
,
∴ ![]()
![]() ,
, ![]() ,
,
∴ ![]()
![]() .
.
由椭圆的定义,得![]() , ∴
, ∴ ![]() ,
, ![]()
在直角三角形![]() 中,
中,
∵ ![]() ,
,
∴ ![]() ∴
∴
![]() .
.
(2)
解:由![]() 可知,
可知,![]() , 故椭圆的方程可化为
, 故椭圆的方程可化为![]() ,焦点为
,焦点为![]() .
.
设![]() ,
,![]() ,
,![]() .
.
方法① ![]() .当直线
.当直线![]() 的斜率存在时,
的斜率存在时,
方法(1)直线![]() 的方程为
的方程为![]() ,代入椭圆方程,得
,代入椭圆方程,得![]()
![]() ,
,
∴ ![]() ,
, ![]() ,
,
∵ ![]() , ∴
, ∴ ![]() ,
, 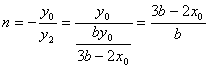 ,
,
同理可得, ![]() ,
,
∴ ![]()
![]() +
+![]() ,
,
∴ ![]() .
.
方法(2)直线![]() 的方程为
的方程为![]() ,代入椭圆方程,得
,代入椭圆方程,得![]()
-![]() ,
,
![]() .
.
∵ ![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() ,
,
∴ ![]() ,
,
同理可得, ![]() ,
,
∴ ![]()
![]() +
+![]() =
=![]() .
.
![]() .当直线
.当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,
,
![]() .
.
综上所述, ![]() 是定值
是定值![]() .
.
方法② ∵ ![]() ,
,![]() , ∴
, ∴ ![]() ,
,![]() ,
,
∴ 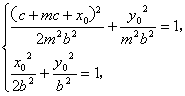
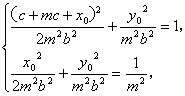
∴ 两式相减可得, ![]() , (∵
, (∵![]()
![]() ,
, ![]()
![]() .
.
同理可得, ![]() , ∴
, ∴ ![]() .
.
![]() .当直线
.当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,
, ![]() .
.
综上所述, ![]() 是定值
是定值![]() .
.
例8.(宿迁市2007届高三年级第四次考试)21题
由原点O向曲线![]() 引切线,切点
引切线,切点![]() 异于点O,再由点
异于点O,再由点![]() 引此曲线的切线,切点
引此曲线的切线,切点![]() 异于点
异于点![]() ,如此继续下去,得到点列
,如此继续下去,得到点列![]() .
.
(1) 求![]() ;
;
(2) 求证数列![]() 为等比数列.
为等比数列.
(1) ∵![]() , ∴
, ∴ ![]()
∴ 过原点O, 切点为![]() 的切线方程为
的切线方程为![]() ,
,
∴ 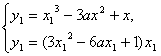 消去
消去![]() 得,
得, ![]()
![]()
∵ ![]() ∴
∴ ![]() .
.
(2) 证明: 设过点![]() 的直线与曲线切于点
的直线与曲线切于点![]() ,
,
则切线方程为![]()
∴ 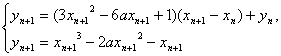
![]()
![]()
![]()
![]()
![]()
![]()
∵ ![]() ,
,
∴ ![]()
![]()
![]()
![]()
![]()
∴ ![]() ,
, ![]()
∵![]() , ∴
, ∴ ![]() ,
,
∴数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
三.调整学生的解题思路,让学生的思维思路活跃而正规
例1. 已知等比数列{![]() }的各项为正数, 数列{
}的各项为正数, 数列{![]() }满足
}满足![]() (
(![]() >0且
>0且![]()
![]() 1),
1), ![]() =18,
=18, ![]() =12.
=12.
(1) 求数列{![]() }的通项公式;
}的通项公式;
(2) 试判断是否存在正整数![]() ,使得当
,使得当![]() >
>![]() 时,
时, ![]() >1恒成立,并说明理由; (0<
>1恒成立,并说明理由; (0<![]() <1)
<1)
(3) 当![]() >12时,
>12时,
求证:![]() +
+ ![]() +
+![]() +...+
+...+![]() <
<![]() .
.
解:(1)∵ 数列{![]() }是各项为正数的等比数列,∴
当
}是各项为正数的等比数列,∴
当![]()
![]() 2时,
2时,![]() =
=![]() -
-![]() =
=![]() 为常数,
为常数,
∴ 数列{![]() }为等差数列。
}为等差数列。
∵ ![]() =18,
=18, ![]() =12, ∴
=12, ∴![]() =-2
=-2![]() +24 .
+24 .
(2) 由(1)知, ![]() =
=![]() -n+12.
-n+12.
① 若0![]()
![]()
![]() 1,则当
1,则当![]()
![]() 12时,
12时, ![]()
![]() 1;当
1;当![]() =12时,
=12时, ![]() =1;当
=1;当![]()
![]() 12时,
12时, ![]()
![]() 1,故当0
1,故当0![]()
![]()
![]() 1时,存在
1时,存在![]() =12,当
=12,当![]()
![]() 12时,
12时, ![]()
![]() 1.
1.
② 若![]()
![]() 1,则当
1,则当![]()
![]() 12时,
12时, ![]()
![]() 1;当
1;当![]() =12时,
=12时, ![]() =1;当
=1;当![]()
![]() 12时,
12时, ![]()
![]() 1,故当0
1,故当0![]()
![]()
![]() 1时,不存在
1时,不存在![]() ,当
,当![]()
![]()
![]() 时,
时, ![]()
![]() 1.
1.
(3) 方法(一)
当![]()
![]() 14时
14时
![]() +
+ ![]() +
+![]() +...+
+...+![]()
=![]() ]
]
<![]()
![]()
![]()
![]()
=![]() [
[![]()
![]()
![]()
![]() +
+![]()
![]()
![]() ]
]
=![]() [
[![]()
![]() ]
]![]()
![]() [
[![]()
![]() ]=
]=![]() .
.
![]()
![]() =
=![]()
=![]() =
=![]()
=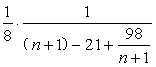 <
< ![]()
当![]() =13时,
=13时,
![]() +
+ ![]() +
+![]() +...+
+...+![]() =
=![]()
<![]() =
=![]()
=![]() =
=![]()
综上所述, 当![]()
![]() 13时,
13时, ![]() +
+ ![]() +
+![]() +...+
+...+![]() <
<![]() .
.
方法(二)
设![]() =
=![]() +
+ ![]() +
+![]() +...+
+...+![]() ,则
,则![]() =
= ![]() +
+![]() +
+![]() +...+
+...+![]()
∴![]() -
-![]() =
=![]() +
+![]() -
-![]() =
=![]()
![]()
<![]()
![]() =
=![]()
![]()
![]()
![]()
![]() <0 .
<0 .
∴![]() <
<![]() , 即{
, 即{ ![]() }单调递减,
}单调递减,
∴![]()
![]()
![]() <
<![]() .
.
例2. 已知数列![]() 满足:
满足: ![]() .
.
(1)
证明: 数列![]() 成等比数列;
成等比数列;
(2)
证明: ![]() .
.
(1) 证明: ∵ ![]() ,
,
∴ ![]() ,
, ![]()
∵ ![]() ∴ 数列
∴ 数列 ![]() 是以2为首项,公比为2的等比数列.
是以2为首项,公比为2的等比数列.
(2) 证明方法①: 由(1)可知, ![]()
∴ ![]() ,
,
解得: ![]() .
.
证明方法②:由(1)可知, ![]()
< ![]() <
< ![]() <
<![]()
∴ ![]()
=![]()
=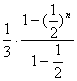 <
<![]()
直线与平面平行的证明: 一般用下列两个基本图形在已知平面内给出一条直线与已知直线平行, 或用面面平行的方法证明.
证明直线与平面平行,如果利用线面平行的判定定理来证明,就必须在已知平面内找到一条直线与已知直线平行,这条直线一般可以过已知直线作一个与已知平面相交的平面而得到,而这个平面可以经过已知直线和与已知直线、已知平面都相交的另一条直线而得到(如图(1)),也可以经过过已知直线上两点且与已知平面相交的两条平行直线而得到(如图(2)). (辅助线的添加问题)
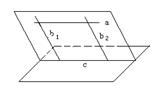
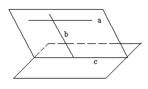
![]()
![]()
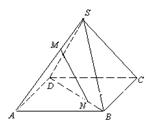
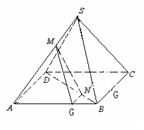
例3.四棱锥![]() 的底面是平行四边形, 点
的底面是平行四边形, 点![]() 在棱SA上,点
在棱SA上,点![]() 在BD上,且
在BD上,且
![]() , 求证:
, 求证: ![]() ∥平面
∥平面![]() .
.
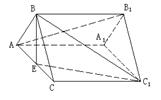 例4.正三棱柱
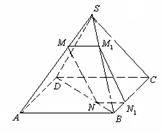
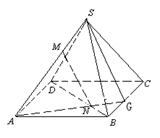
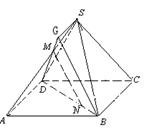
例4.正三棱柱![]() 中,E为AC的中点.求证:
中,E为AC的中点.求证: ![]() ‖平面
‖平面![]() .
.
分析: 先利用图形(1)在平面![]() 内给出与直线
内给出与直线![]() 平行的直线.
平行的直线.
本例中与直线![]() 、平面
、平面![]() 都相交的直线有
都相交的直线有![]() 、
、![]() 、
、![]() 、
、![]() .
.
① ![]() 与
与![]() 确定平面
确定平面![]() ,
,
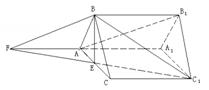 显然点
显然点![]() 是平面
是平面![]() 与平面
与平面![]() 的一个公共点,
的一个公共点,
延长![]() 、
、![]() 相交于点F,连结BF,则直线BF就是经过直线
相交于点F,连结BF,则直线BF就是经过直线![]() 的平面
的平面![]() 与平面
与平面![]() 的交线,只要证明直线
的交线,只要证明直线![]() ‖直线
‖直线![]() ,就可得
,就可得![]() ‖平面
‖平面![]() .
.
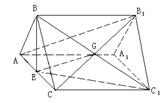 ②
② ![]() 与
与![]() 确定平面
确定平面![]() ,
,
显然点E是平面![]() 与平面
与平面![]() 的一个公共点,
的一个公共点,
连结![]() ,设直线
,设直线![]() 与直线
与直线![]() 的交点为G, 连结EG,则直线EG就是平面
的交点为G, 连结EG,则直线EG就是平面![]() 与平面
与平面![]() 的交线,只要证明直线
的交线,只要证明直线![]() ‖直线
‖直线![]() ,就可得
,就可得![]() ‖平面
‖平面![]() .
.
③ ![]() 与
与![]() 确定平面
确定平面![]() ,显然点
,显然点![]() 是平面
是平面![]() 与平面
与平面![]() 的一个公共点,因此,这时的证明方法与①相同.
的一个公共点,因此,这时的证明方法与①相同.
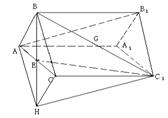 ④
④ ![]() 与
与![]() 确定平面
确定平面![]() ,
,
显然点![]() 是平面
是平面![]() 与平面
与平面![]() 的一个公共点,延长
的一个公共点,延长![]() 到
到![]() ,使
,使![]() ,连结
,连结![]()
![]() ,则
,则![]() 就是平面
就是平面![]() 与平面
与平面![]() 的交线,只要证明直线
的交线,只要证明直线![]() ‖直线
‖直线![]() ,就可得
,就可得![]() ‖平面
‖平面![]() .
.
下面再利用图形(2)在平面![]() 内给出与直线
内给出与直线![]() 平行的直线.
平行的直线.
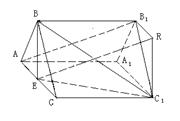 ① 直线AC是过点A且与平面
① 直线AC是过点A且与平面![]() 相交于点E的一条直线,下面我们在给出一条过点
相交于点E的一条直线,下面我们在给出一条过点![]() 且与AC平行、与平面
且与AC平行、与平面![]() 相交的另一条直线.
相交的另一条直线.
在平面![]() 内过点
内过点![]() 作
作![]() ‖
‖![]() ,过点
,过点![]() 作
作![]() ,连结
,连结 ![]() ,只要证明
,只要证明![]() 就是经过直线
就是经过直线![]() 的平面与平面
的平面与平面![]() 的交线,且直线
的交线,且直线![]() ‖
‖![]() ,就可得
,就可得![]() ‖平面
‖平面![]() .
.
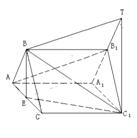 ② 直线AB是过点A且与平面
② 直线AB是过点A且与平面![]() 相交于点B的一条直线,下面我们在给出一条过点
相交于点B的一条直线,下面我们在给出一条过点![]() 且与AB平行、与平面
且与AB平行、与平面![]() 相交的另一条直线.
相交的另一条直线.
在平面![]() 内延长
内延长![]() 到T,使
到T,使![]() =
=![]() ,连结
,连结![]() 、
、![]() ,只要证明
,只要证明![]() 就是经过直线
就是经过直线![]() 的平面与平面
的平面与平面![]() 的交线,且直线
的交线,且直线![]() ‖
‖![]() ,就可得
,就可得![]() ‖平面
‖平面![]() .
.
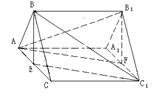 本例也可以利用面面平行的性质证明
本例也可以利用面面平行的性质证明![]() ‖平面
‖平面![]() .
.
取![]() 的中点F, 连结AF、B1F,证明平面
的中点F, 连结AF、B1F,证明平面![]() ‖平面
‖平面![]() ,就可得
,就可得![]() ‖平面
‖平面![]() .
.
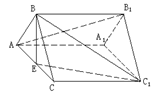
本例也可以用基底向量法给出证明.
证明: 取![]() 为一组基底.
为一组基底.
![]()
![]() ,
,![]() ,
,
![]() =
=![]() ,
,
设![]() =
=![]()
![]()
![]()
![]() , 则
, 则![]() =
=![]() (
(![]() )
)![]()
![]()
=![]()
∴ 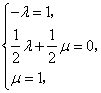 ∴
∴ ![]() ,
, ![]() , ∴
, ∴ ![]() =-
=-![]() +
+![]() ,
,
∴![]() ‖平面
‖平面![]() .
.
四.让学生知道练什么,使学生的操作技能达到一定层次
例1.求函数![]() 在
在![]() 上的最小值为-2,求实数
上的最小值为-2,求实数![]() 的取值 .
的取值 .
例2.已知函数![]() 的最小值是
的最小值是![]() ,求实数
,求实数![]() 的取值 .
的取值 .
解:若![]() ,则函数的定义域为[0,+
,则函数的定义域为[0,+![]() ),且为增函数,故
),且为增函数,故![]() ,得
,得![]() ;
;
若![]() ,则函数的定义域为[-a,+
,则函数的定义域为[-a,+![]() ),且为增函数,故
),且为增函数,故![]() ,得
,得![]() ,
,
∴
![]() .
.
例3. (盐城市2008届高三第一次调研卷)题12
已知函数![]() 在
在![]() 的最大值为
的最大值为![]() ,求实数
,求实数![]() 的取值 .
的取值 . ![]()
例4. (苏州市2008届高三第一次调研测试)题19
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且没卖一件产品需向税务部门上交![]() (
(![]() 为常数,
为常数,![]() )元的税收.设每件产品的日销售价为
)元的税收.设每件产品的日销售价为![]()
![]() 元,根据市场调查, 日销售量与
元,根据市场调查, 日销售量与![]() 为自然对数的底数)成反比例.已知每件产品的日销售价为40元时, 日销售量为10件.
为自然对数的底数)成反比例.已知每件产品的日销售价为40元时, 日销售量为10件.
(1) 求该商店的日利润![]() 元与每件产品的日销售价
元与每件产品的日销售价![]() 元的函数关系式;
元的函数关系式;
(2) 当没件产品的日销售价为多少时, 该商店的日利润![]() 最大,并求出
最大,并求出![]() 的最大值.
的最大值.
解: (1) ![]() =
=![]()
![]() ;
;
(2) ![]() =
=![]()
∵ ![]() , ∴
, ∴ ![]()
① 若![]() ,则
,则![]() ,
, ![]()
![]() (当且仅当
(当且仅当![]() 是
是
取等于号),
这时,函数![]() 在
在![]() 上为减函数,
上为减函数, ![]() 的最大值为
的最大值为![]() ,即10
,即10![]() ;
;
② 若![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]()
![]() ,当
,当
![]() 时,
时, ![]()
![]() ,
,
这时, 函数![]() 在
在![]() 上为增函数, 在
上为增函数, 在![]() 上为减函数,故函数的最大值为
上为减函数,故函数的最大值为![]() ,即
,即![]()
∴ 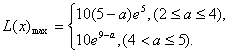
例5.求函数![]() 的最小值.
的最小值.
例6.设a为实数, 函数![]() .
.
(1) 讨论函数![]() 的奇偶性; (2) 求
的奇偶性; (2) 求![]() 的最小值.
的最小值.
解(1): 若函数![]() 为奇函数,
为奇函数,
则![]() +
+![]() =0,即(
=0,即(![]() )+(
)+(![]() ,这是不可能的,故函数
,这是不可能的,故函数![]() 不可能为奇函数.
不可能为奇函数.
若函数![]() 为偶函数,
为偶函数,
则![]() -
-![]() =0,即(
=0,即(![]() )-(
)-(![]() ,
,
∴ 等式![]() 对任意
对任意![]() 都成立, 故
都成立, 故![]() ,即
,即![]() 时函数
时函数![]() 为偶函数.
为偶函数.
(2) 函数![]() 可以化为
可以化为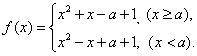
方法(一) (整体求解)
① 若![]() ,则函数
,则函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 上是增函数, 故函数
上是增函数, 故函数![]() 的最小值为
的最小值为![]()
![]() .
.
②
若![]() ,则函数
,则函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 上是增函数, 故函数
上是增函数, 故函数![]() 的最小值为
的最小值为![]() .
.
③
若![]() ,则函数
,则函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 上是增函数, 故函数
上是增函数, 故函数![]() 的最小值为
的最小值为![]()
![]() .
.
方法(二) (分段讨论)
① 当![]() 时,
时, ![]() ,
,
若 ![]() ,则函数
,则函数![]() 在
在![]() 是减函数, 故函数
是减函数, 故函数![]() 的最小值为
的最小值为
![]() ,
,
若![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]()
![]() .
.
② 当![]() 时,
时, ![]() ,
,
若 ![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]()
![]() .
.
若![]() ,则函数
,则函数![]() 在
在![]() 是增函数, 故函数
是增函数, 故函数![]() 的最小值为
的最小值为
![]() ,
,
∴ 若![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]()
![]() ;
;
若![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]() ;
;
若![]() ,则函数
,则函数![]() 的最小值为
的最小值为![]()
![]() .
.
例7.求使关于![]() 的不等式
的不等式![]() 在
在![]() 恒成立的实数
恒成立的实数![]() 的取值范围.
的取值范围.
例8.若不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是 .
的取值范围是 . ![]()
例9.已知二次函数![]() ,对于
,对于![]() ,
,![]() 成立,试求实数
成立,试求实数![]() 的取值范围.
的取值范围.
解: 由题设可知, ![]() ,
,
① 若![]() , 则
, 则![]() ;
;
② 若![]() , 则
, 则![]() ,
,
∴ ![]() ,
, ![]() ,
, ![]() .
.
例10. (南京市2008届高三第一学期期末调研卷)题20
已知数列![]() 是公差为
是公差为![]() 的等差数列,它的前
的等差数列,它的前![]() 项和为
项和为![]() ,
,![]() .
.
(1) 求公差![]() 的值;
的值;
(2) 若![]() ,求数列
,求数列![]() 中的最大项和最小的项;
中的最大项和最小的项;
(3) 若对任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
解:(1)∵
![]() ∴
∴ ![]() ,解得,
,解得,![]() .
.
(2) 若![]() ,则
,则![]() ,
,
∴ 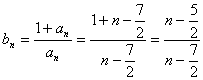 =
=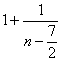
∴ 当![]() 时,
时,![]() 取最大值3, 当3时,
取最大值3, 当3时,![]() 取最大值-1.
取最大值-1.
(3) ![]() =1+
=1+![]() ,
,
∵ ![]() , ∴ 1+
, ∴ 1+![]()
![]() 1+
1+![]() ,
, ![]()
![]()
![]() ,
,
方法①:![]()
若![]() ,则
,则![]() ,
,![]() ,∴
,∴ ![]() ;
;
若![]() ,则
,则![]()
若![]() ,则
,则![]() ,
,![]() .
.
综上所述, ![]() .
.
方法②:考虑函数![]()
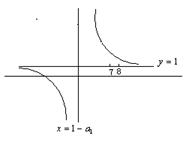
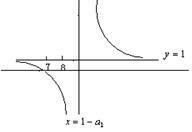
由此可知, ![]() , ∴
, ∴ ![]() .
.
例11. (南京市2008届高三第一学期期末调研卷)题18
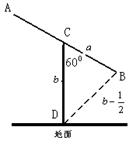 某建筑的金属支架如图所示,根据要求
某建筑的金属支架如图所示,根据要求![]() 至少长2.8
至少长2.8![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 到
到![]() 的距离比
的距离比![]() 的长小0.5
的长小0.5![]() ,
,![]() .已知金属支架每米的价格一定,问怎样设计
.已知金属支架每米的价格一定,问怎样设计![]() ,
,![]() 的长, 可使建造这个支架的成本最低?
的长, 可使建造这个支架的成本最低?
解:设![]()
![]() 则
则![]() ,
,![]()
由题设可知,在![]() 中,
中,![]() .
.
设![]()
![]() ,
,
方法①:则由![]() 知,
知,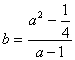 ,
,
∴ ![]()
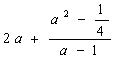
=![]()
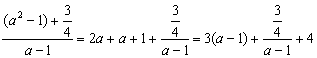
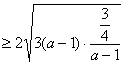 (当且仅当
(当且仅当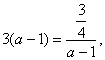 即
即![]() 时等于号成立)
时等于号成立)
=7
这时![]() ,即
,即![]() =3,
=3,![]() =4时建造这个支架的成本最低.
=4时建造这个支架的成本最低.
方法②:![]() .
.
![]() ,
,
则![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
,
∵ ![]() , ∴
, ∴ ![]() .
.
当![]() 时,
时, ![]() , 即
, 即![]() ,
, ![]() ,
, ![]() ,
,
![]() ,故7为
,故7为![]() 的最小值. 即
的最小值. 即![]() =3,
=3,![]() =4时建造这个支架的成本最低.
=4时建造这个支架的成本最低.
方法③:![]() .
.
![]() ,
,
则![]() ,
, ![]()
令![]()
![]() ,则函数
,则函数![]() 的图象与
的图象与![]() 轴在
轴在![]() 上有公共点.
上有公共点.
∴ ![]() 或
或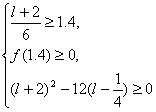 解得,
解得,![]() 或
或![]() ,即
,即![]() .
.
当![]() 时,
时, ![]() ,
,![]() , 即
, 即![]() =3,
=3,![]() =4时建造这个支架的成本最低.
=4时建造这个支架的成本最低.