化直线
的参数方程
（t为参数）为普通方程，并求倾斜角，
化直线
的普通方程
＝0为参数方程，并说明参数的几何意
义,说明∣t∣的几何意义.
已知直线
过点M0（1，3），倾斜角为
，判断方程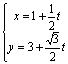
（t为参数）和方程
（t为参数）是否为直线的参数方程？
直线的参数方程能否化为标准形式？
写出经过点M0（－2，3），倾斜角为
的直线的标准参数方程，并且
求出直线上与点M0相距为2的点的坐标.
直线
（t为参数）的倾斜角
.
1、 求过点(6,7),倾斜角的余弦值是
的直线的标准参数方程.
2、 直线的方程：
（t为参数），那么直线的倾斜角( )
A 65° B 25° C 155° D 115°
3、 直线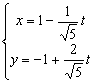
（t为参数）的斜率和倾斜角分别是( )
A) －2和arctg(－2) B) －
和arctg(－
)
C) －2和
－arctg2 D) －和－arctg
4、 已知直线
（t为参数）上的点A、B 所对应的参数分别为t1,t2，点P分线段BA所成的比为
（≠－1），则P所对应的参数是
.
5、直线的方程： 
（t为参数）A、B是直线上的两个点，分别对应参数值t1、t2，那么AB等于( )
A ∣t 1－t 2∣ B 
∣t 1－t 2∣ C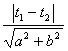 
D ∣t 1∣+∣t 2∣
已知直线：
(t为参数)与直线m：
交于P点，求点M(1,－5)到点P的距离.
7、 直线
(t为参数)与椭圆
交于A、B两点，则AB等于(
)
A 2
B 
C 2
D 
8、直线 （t为参数）与二次曲线A、B两点，则AB等于( )
A t1+t2 B t1＋t2 C t1－t2 D 
9、 直线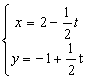
(t为参数)与圆
有两个交点A、B，若P点的坐
标为(2,-1),则PA·PB=
10、过点P(6,
)的直线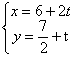
(t为参数)与抛物线y2=2
相交于A、B两点，
则点P到A,B距离之积为 .