专题七：高考数学向量与向量法复习
一．考点与回顾
1．平面向量是教材新增内容之一，其数形结合的特点使得它成为高中数学教学中继函数之后的第二条主线．向量是数学中重要概念之一．向量为解决数学、物理中的问题提供了新的工具.
2.有关平面向量的考查热点在两个方面：一是对向量基本概念、基本运算的考查；二是对向量的工具作用的考查，即运用向量知识解决平面几何、解析几何、三角函数等中的简单问题．
3.随着新教材的普遍使用，“向量”将会成为命题热点，一般选择、填空题重在考查平面向量的概念、数量积及其运算律，解答题重在考查平面向量的综合应用，常与函数、三角函数、平面解析几何、立体几何、数列等知识结合起来考查．对本专题的复习应立足基础，强化运算，重视应用．数形结合思想在本专题中将得到淋漓尽致的体现．
4．在2007年全国各省市的高考试卷中，向量在各种题型中都有出现.选择题、填空题的形式主要考查向量的模、夹角、数量积以及向量间的关系等基础知识与基本技能．而在解答题中则主要与三角形、函数、空间几何体、圆锥曲线等结合、交汇.
5．按教材编排体系，解三角形在本专题中复习，即正、余弦定理(及其各种变形)运用于三角形形状的判断、证明三角形中的边角恒等式、定比分点及求解有关实际应用问题这也是高考热点之一．
6．对于学有余力的学生，可以适当补充简单的空间解析几何知识，如空间直角坐标系中平面的方程(特别是平面的截距式方程)，点到平面的距离公式等.
7．知识网络
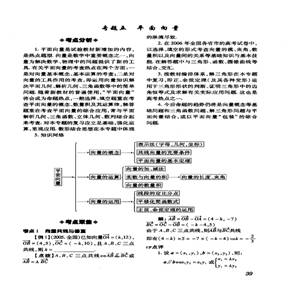
二．经典例题剖析
考点一：向量的概念与运算
例题1：下面有四个关于向量数量积的关系式：
①0·0＝0；②(a·b)·c＝a·(b·c)；③a·b＝b·a；④a·b≤a·b
其中正确的是( )
A.①② B.②③ C.③④ D.①③
解析：根据向量运算法则，①和③是正确的.
对于②，(a·b)·c是一个与向量c平行的向量，而a·(b·c)是一个与向量a平行的向量，通常情况下不正确；对于④，a·b是一个正实数，而a·b可能是一个负实数.
答案：D
点评：从向量的基本运算法则出发，细心判断.这里要特别注意向量0与实数0的区别.
例题2：平行四边形OACB中，BD＝BC，OD与BA交于E，求证：BE＝BA
证明：设E’是AB上一点，且BE’＝BA
只需证E、E’重合即可，
设，则
∵
∴3(
∴
∴，∴O、E’、D三点共线，即E、E’重合
∴BE＝BA
点评：用向量方法证明平面几何问题，首先是选择一组适当的基底向量，然后再设法将其余相关向量都用基底向量表示出来，这样，相关点、线关系就能很容易第凸现出来.
考点二：定比分点与解三角形
例题3：已知平行四边形ABCD的三个顶点坐标分别是A(－2，1)，B(3，4)，C(－1，3)，则第四个顶点D的坐标为( )
A.(2，2) B.(－6，0) C.(4，6) D.以上都不对
解析：本题只需要抓住平行四边形的两条对角线互相平分，
于是设D(x,y)，有－2＋(－1)＝3＋x且1＋3＝4＋y
从而x＝－6,y＝0
答案：B
点评：利用平面几何性质及中点坐标公式，是解决本题的要点.
例题4：已知C为线段AB上一点，P为直线AB外一点，满足＝2，－＝2，
，I为PC上一点，且＝＋λ(
)(λ＞0)，则
的值为_______.
[点拨]确定PC、AI分别为∠APB、∠BAP的平分线，进而确定I在三角形中的位置.
解：
cos∠APC
cos∠BPC
所以∠APC＝∠BPC，即PC平分∠APB
∵
(λ＞0)
∴
(λ＞0)
又
均为单位向量，由向量的平行四边形法则，知AI平分∠PAB
又I在PC上，故I是△ABP的内心
又
cos∠IBD＝
(D为⊙I与AB的切点)
由
＝2
又
解得：cos∠IBD＝＝－1
[点评]1、三角形中四心的向量表示：
2、本题通过内切圆的切点D找出相关的数量关系，技巧性较强，考查圆的切线性质.
考点三：向量与立体几何
例题5：如图，直四棱柱ABCD－A1B1C1D1中，底面ABCD是等腰梯形，AB∥CD，AB＝2DC＝2，E为BD1的中点，F为AB的中点.
(1)求证：EF∥平面ADD1A1；
(2)若BB1＝，求A1F与平面DEF所成角的大小.
解析：(1)连结AD1，在△ABD1中，
∵E、F分别是BD1、AB的中点，∴EF∥AD1.
又EFË平面ADD1A1
∴EF∥平面ADD1A1
(2)建立如图所示的空间直角坐标系D－xyz
(DG是AB边上的高)
则有A1()，F(，0)
D1(0，0，)，B(，0)
∴E()
设平面DEF的法向量为＝(x，y，z)
则Þ
解得y＝－x，z＝x
取非零法向量＝(1，－，)
∴A1F与平面DEF所成的角即是所成锐角的余角
由cos<>＝＝＝－
∴A1F与平面DEF所成教的大小为－arccos，即arcsin.
点评：立体几何中，二面角问题几乎每年必考，几何法也有很多解决方法，如直接法、垂面法、三垂线法、面积射影法等等，这些方法都离不开严密的逻辑证明.而向量法则以算代证，从一定程度上减轻了对逻辑思维的要求，但也应该注意到，向量法计算较为烦琐，运算量较大，必须小心谨慎，否则也极易出现差错.
例题6：如图，已知平行六面体ABCD－A1B1C1D1的底面ABCD是菱形，且∠C1CB＝∠C1CD＝∠
BCD＝60°
⑴证明：C1C⊥BD；
⑵假定CD＝2，CC1＝，记面C1BD为α，面CBD为β，求二面角α－BD－β的平面角的余弦值；⑶当的值为多少时，能使A1C⊥平面C1BD？请给出证明.
⑴证明：连结A1C1、AC，AC和BD交于O，连结C1O
∵四边形ABCD是菱形
∴AC⊥BD，BC＝CD
又∵ ∠BCC1＝∠DCC1，C1C＝C1C，
∴ △C1BC≌△C1DC
∴ C1B＝C1D
∵DO＝OB∴ C1O⊥BD
但AC⊥BD，AC∩C1O＝O
∴ BD⊥平面AC1，
又CC1∩平面AC1∴ CC1⊥BD
证法二：设CD、CB、CC1三个方向上的单位向量分别为、、
则、、两两成60°角
且，,
则
于是＝mn(＝0
故 CC1⊥BD
⑵解：由⑴知AC⊥BD，C1O⊥BD
∴ ∠C1OC是二面角α－BD－β的平面角
在△C1BC中，BC＝2，C1C＝，∠BCC1＝60°
∴ C1B2＝22＋()2－2×2××cos60°＝
∵∠OCB＝60°，∴ OB＝BC＝1
∴ C1O2＝C1B2＝OB2＝
∴ C1O＝，即C1O＝C1C
作C1H⊥OC，垂足为H.
∴点H是OC的中点，且OH＝，
∴ cos∠C1OC＝.
⑶当＝1时，能使A1C⊥平面C1BD
证明一：∵＝1
∴ BC＝CD＝C1C
又∠BCD＝∠C1CB＝∠C1CD
由此可推得BD＝C1B＝C1D
∴三棱锥C－C1BD是正三棱锥.
设A1C与C1O相交于G.
∵ A1C1∥AC，且A1C1：OC＝2：1
∴ C1O：GO＝2：1
又C1O是正三角形C1BD的BD边上的高和中线，
∴点G是正三角形C1BD的中心.
∴ CG⊥平面C1BD
即 A1C⊥平面C1BD.
证明二：由⑴知，BD⊥平面AC1
∵ A1C∩平面AC1，∴ BD⊥A1C.
当＝1时，平行六面体的六个面是全等的菱形.
同 BD⊥AC1的证法可得BC1⊥A1C
又BD⊥BC1于B
∴ A1C⊥平面C1BD
证法三：设＝x，即
由(2)可知：BD⊥平面AA1C1C，∴BD⊥A1C
由线面垂直得判定定理，知：如果A1C⊥DC1，则A1C⊥平面C1BD成立.
∵＝m＋m＋
＝－m＋
又∵＝0
∴(m＋m＋)(－m＋e3)＝0
展开整理得：－＝0
∴x＝1
以上各步可逆，所以x＝1时，即＝1时，A1C⊥平面C1BD
点评：空间向量中，基底向量的使用是学生的一个弱项，许多学生动辄建立坐标系，对于垂直条件“不足”的问题往往感到手足无措，本题就是一例.从本题的向量证明方法中，还可以明确看到不仅解决了几何证法中“有一解”的问题，而且明确了“只有一解”的充要关系.
考点四：向量与其他知识点综合问题
例题7：已知A、B、C是△ABC三内角，向量
且m·n＝1
（1）求角A
（2）若
解析：（1）∵
∴
即
，
sin(A－)＝
∵
∴
∴A＝
（2）由题知
，整理得sin2B－sinBcosB－2cos2B＝0
∴cosB≠0 ∴tan2B－tanB－2＝0
∴tanB＝2或tanB＝－1
而tanB＝－1使cos2B－sin2B＝0，舍去
∴tanB＝2
∴tanC＝tan[π－(A＋B)]＝－tan(A＋B)
点评：向量与三角函数的综合问题是当前的一个热点，但通常难度不大，一般就是以向量的坐标形式给出与三角函数有关的条件，并结合简单的向量运算，而考查的主体部分则是三角函数的恒等变换，以及解三角形等知识点.
例题8：设向量＝(1，0)，＝(0，1)，＝(x＋m)＋y，＝(x－m)＋y，且＋＝6，0＜m＜3，x＞0，y∈R.
(1)求动点P(x，y)的轨迹方程；
(2)已知点A(－1，0)，设直线y＝(x－2)与点P的轨迹交于B、C两点，问是否存在实数m，使得？若存在，求出m的值；若不存在，请说明理由.
解析：(1)∵＝(1，0)，＝(0，1)，＋＝6
∴＝6
上式表示动点P(x，y)到两定点F1(－m，0)和F2(m，0)的距离之和为6
而0＜m＜3，故F1F2＜6
故P点轨迹为以F1、F2为焦点，长轴长2a＝6的椭圆，
于是a＝3，c＝m，b2＝9－m2
故P点轨迹方程为＝1(x＞0，0＜m＜3)
(2)设B(x1，y1)，C(x2，y2)
∵＝(x1＋1，y1)，＝(x2＋1，y2)，
∴＝x1x2＋(x1＋x2)＋1＋y1y2
而y1y2＝(x1－2)·(x2－2)＝[x1x2－2(x1＋x2)＋4]
∴＝x1x2＋(x1＋x2)＋1＋[x1x2－2(x1＋x2)＋4]
＝[10x1x2＋7(x1＋x2)＋13]
若存在实数m，使得成立
则由[10x1x2＋7(x1＋x2)＋13]＝
Þ 10x1x2＋7(x1＋x2)＋10＝0 ……①
由
消去y得：(10－m2)x2－4x＋9m2－77＝0 ……②
由②有
由①④⑤解得m2＝＜9，且此时△＞0
但由⑤，有9m2－77＝＜0与题设矛盾
∴不存在符合题意的实数m，使得.
点评：向量与解析几何的综合问题，通常是利用向量的几何特性来描述解析几何中的图象性质，一般解决办法是利用向量的坐标表示，“尽快”转化为纯解析几何问题求解.当然也不排除利用平面几何性质，直接将向量特征转化为几何特征，更快地得到问题的解.
三．方法总结与08年高考预测
(一)方法总结
1.以“基底”形式出现的向量问题通常将题中的化为以某一点为统一起点，再进行向量运算会非常方便；
2.以坐标形式出现的向量问题可以尽可能利用解析思想，转化为函数或方程方法求解；
(二)08高考预测
预计向量基本概念等基础问题和三角函数问题、解三角形问题与平面向量结合，通常为选择题或填空题；而用向量“包装”的综合问题，如立体几何、解析几何等，通常为解答题.难度以中档题为主.
四．强化训练
(一)选择题
1.如图，D，E，F分别是△ABC的边AB，BC，CA的中点，则下列等式中成立的是( )
A. B.＝0
C. D.
答案：A
2.若三个点P(1，1)，A(2，－4)，B(x，－9)共线，则x＝( )
A.－1 B.3 C. D.51
答案：B
3.若向量＝(cosα，sinα)，＝(cosβ，sinβ)，则与一定满足( )
A.夹角为α－β B.(＋)⊥(－) C.∥ D.⊥
解：＋＝(cosα＋cosβ，sinα＋sinβ)
－＝(cosα－cosβ，sinα－sinβ)
∴(＋)·(－)＝cos2α－cos2β＋sin2α－sin2β＝0
选B
4.设点P分有向线段的比为λ，且＝3，则λ＝( )
A.4或－2 B.－3或1 C.－4或2 D.－3或－1
答案：C
5.若＝b，则∠AOB平分线上的向量为( )
A. B.λ(λ由确定)
C. D.
答案：B
6.将函数y＝x2＋4x＋5的图像按向量a经过一次平移后得到y＝x2的图像，则a＝( )
A.(2，－1) B.(－2，1) C.(－2，－1) D.(2，1)
答案：A
7.设a、b是平面内两个不共线的向量，且＝2a＋pb，＝a＋b，＝a－2b，若A、B、D三点共线，则实数p的值为( )
A、1 B、2 C、－2 D、－1
答案：D
8.如果e1、e2是平面α内的一组基底向量，那么下列说法正确的是( )
A、若实数λ1、λ2使得λ1e1＋λ2e2＝0，则λ1＝λ2＝0
B、空间中任意向量a都可以表示为a＝λ1e1＋λ2e2，其中λ1、λ2∈R
C、λ1e1＋λ2e2不一定在平面α内，其中λ1、λ2∈R
D、对于平面α内的任意一个确定向量a，使得a＝λ1e1＋λ2e2的实数λ1、λ2不止一对.
答案：A
9.已知a＝2sin15€，b＝4cos15，如果a与b的夹角为30，则a·b＝( )
A、6 B、4 C、 D、1
答案：C
10.已知点A(2，0)，B(2,2),点C满足＝(cosθ,sinθ)(θ∈R)，则向量与向量夹角的取值范围是( )
A、[0,] B、[,] C、[,] D、[,]
答案：D
11.已知抛物线方程为y2＝2x，一直线过抛物线的焦点，且与抛物线相交于A、B两点，则＝( )
A、 B、－ C、3 D、－3
解：设A(y12,y1),B(y22,y2)，即＝(y12,y1),＝(y22,y2)
对于过焦点的直线，所得两点满足y1y2＝－p2＝－1
∴＝(y12,y1)·(y22,y2)＝y12y22＋y1y2＝－
答案：B
12.如图，一条船从岸边A点出发，沿垂直于河岸的方向航行，船相对于水流的速度为V1,水流速度为V2(V1＞V2)，则船的实际行驶速度为( )
A、 B、
C、 D、
解：根据题意及向量加法的几何意义，△ABC为直角三角形
故V＝
答案：B
(二)填空题
13.已知△ABC中，＝b，a·b＜0，S△ABC＝，a＝3，b＝5，则a与b的夹角为( )
答案：150
14.设m＝(a,b)，n＝(c,d)，定义一种运算⊙，使得m⊙n＝(ac－bd，ad＋bc)，现已知p＝(1,2)，且p⊙q＝(－4，－3)，则q＝__________
答案：(－2,1)
15.已知△ABC的三个顶点为A(4，5)，B(－2，－1)，C(7，2)，M分为1∶2，N分为1∶2，则S△AMN∶S△ABC＝_____________
答案：2∶9
16.平面直角坐标系中，O为坐标原点，已知两点A（3，1），B（－1，3），若点C满足
，其中α、β∈R，且α+β=1，则点C的轨迹方程为_________________.
解析：设
=（x，y），
=（3，1），
=（－1，3），α=（3α，α），
β=（－β，3β），又α+β=（3α－β，α+3β）
∴（x，y）=（3α－β，α+3β），∴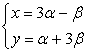
又α+β=1 因此可得x+2y=5.
答案：x+2y=5
(三)解答题
17.如图，三角形ABC中，点M是BC的中点，点N在边AC上，AN＝2NC，AM与BN相交于点P，求AP:PM的值.
解：设，则
又设
则由得
∴ Þ
∴AP:PM＝4∶1
18.设平面内两个向量a、b互相垂直，且a＝2，b＝1，又k与t是两个不同时为0的实数，
(1)若x＝a＋(t－3)b与y＝－ka＋tb垂直，求k关于t的函数关系式k＝f(t)
(2)求函数k＝f(t)的最小值.
解：(1)因为a、b互相垂直，故a·b＝0，
又x、y互相垂直，故x·y＝0，即(a＋(t－3)b)·(－ka＋tb)＝0
Þ －ka2－k(t－3)a·b＋ta·b＋t(t－3)b2＝0
∵a＝2，b＝1，a·b＝0，
∴－4k＋t2－3t＝0
即k＝f(t)＝(t2－3t)
(2)由(1)知,k＝(t－)2－
∴当t＝时，函数的最小值为－.
19.如图：在正方体ABCD－A1B1C1D1中，E、F分别是BB1、CD的中点，棱长AA1＝a.
(1)证明：AD⊥D1F；
(2)求AE与D1F所成的角；
(3)求四面体A1D1EF的体积。
解法一：设基底{}
∵ ABCD－A1B1C1D1是正方体，棱长为a
∴ ＝a
且
(1)∵
＝
＝0
∴
即 AD⊥D1F
(2)∵ cos<
＝
＝
＝0
∴ <>＝90º
也就是AE与D1F所成角为90º.
(3)取CC1中点G，因为EG∥平面A1D1F，则四面体A1D1EF的体积等于四面体A1D1GF的体积.
即VA1D1EF＝VA1D1FG＝S△D1FG·A1D1＝×a2×a＝a3.
解法二：以D为坐标原点，DA、DC、DD1分别为x、y、z轴建立空间直角坐标系。
于是有：D(0，0，0)，A(a，0，0)，D1(0，0，a)，E(a，a，)，F(0，，0)
∴ ＝(0，0，0)－(a，0，0)＝(－a，0，0)
＝(0，，0)－(0，0，a)＝(0，，－a)
＝(a，a，)－(a，0，0)＝(0，a，)
＝(0，，0)－(a，a，)＝(－a，－，－)
(1)∵ ＝(－a，0，0)·(0，，－a)＝0
∴
即 AD⊥D1F
(2)∵ cos<＝0
∴ <>＝90º
(3)设平面A1D1F的一个法向量为＝(x，y，z)
由且＝(a，0，0)
∴x＝0
由且＝(0，，－a)
得y－2z＝0
不妨设y＝2，z＝1，则＝(0，2，1)
于是面A1D1F上的高为d＝＝＝
而S△A1D1F＝A1D1×D1F＝a×a＝a2
∴V＝×a2×＝a3.
20.已知两点M（－1，0），N（1，0），且点P使
成公差小于零的等差数列.
（1）点P的轨迹是什么曲线？
（2）若点P坐标为（x0，y0），θ为
与
的夹角，求tanθ.
解：（1）记P（x，y），由M（－1，0），N（1，0）得=－
=（－1－x，－y），
=－
=（1－x，－y），
=－
=（2，0）
∴·=2（1+x），·=x2+y2－1，·=2（1－x）.
于是，·，·，·是公差小于零的等差数列等价于
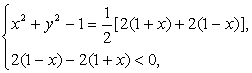
即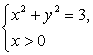
所以，点P的轨迹是以原点为圆心，
为半径的右半圆.
（2）点P的坐标为（x0，y0）.
·=x02+y02－1=2.
·=
.
∴cosθ=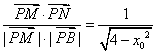
由θ∈[0,π]，sinθ＝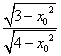
所以tanθ＝＝y0
21.如图，在四棱锥E－ABCD中，
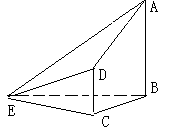
AB⊥平面BCE，CD⊥平面BCE，
AB＝BC＝CE＝2CD＝ 2, ∠BCE＝1200．
(1)求证：平面ADE⊥平面ABE ；
(2)求点C到平面ADE的距离.
解法一:取BE的中点O,连OC.
∵BC＝CE, ∴OC⊥BE.又AB⊥平面BCE.
以O为原点建立空间直角坐标系O－ｘｙｚ如图，
则由已知条件有:
,
,
,
设平面ADE的法向量为ｎ=
，
则由ｎ·
及ｎ·
可取ｎ
又AB⊥平面BCE. ∴AB⊥OC.OC⊥平面ABE
∴平面ABE的法向量可取为m＝
.
∵ｎ·m·＝0,
∴ｎ⊥m∴平面ADE⊥平面ABE.
⑵点C到平面ADE的距离为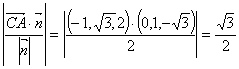
22.已知＝(x，0)，＝(1，y)，且(.
(1)求点P(x，y)的轨迹C的方程；
(2)若直线l：y＝kx＋m(m≠0)与曲线C交于A、B两点，D(0，－1)，且有AD＝BD，试求m的取值范围.
解：(1)由(
得2－32＝0，即x2－3y2＝0
故点P(x，y)的轨迹C的方程为－y2＝1
(2)由方程组消去y得：(1－3k2)x2－6kmx－3m2－3＝0
显然1－3m2≠0，△＝(6km)2－4(1－3k2)(－3m2－3)＝12(m2＋1－3k2)＞0 (*)
设x1、x2为方程(*)的两个根，则x1＋x2＝
∴x0＝，y0＝kx0＋m＝
即AB的中点坐标为()
∴线段AB的垂直平分线方程为：y－＝(－)(x－)
将D(0，－1)代入并化简得：4m＝3k2－1
故m、k满足
消去k2得：m2－4m＞0
∴m＜0或m＞4
又∵4m＝3k2－1＞－1，∴m＞－
所以 m∈(－，0)∪(4，＋∞).
五、复习建议
1.向量部分的复习应该注重向量的工具作用，紧紧围绕数形结合思想，扬长避短，解决问题；
2.向量与立体几何的交汇是近年来的考查热点，命题者往往会将试题命制为几何法与向量法都能求解，但我们一定要注意他们各自的优势和弱点：向量法下手容易，思路简单，但相对计算复杂；几何法过程通常较为简洁，但下手有一定的难度，过程中对逻辑思维要求较高.因此，我们不能一见到立体几何问题就一味使用向量法，还是要结合试题本身特点，在几何法与向量法中做出正确的选择；